数学竞赛数学史演讲稿（我从事数学科普写作的经验与启示）

本文为“2022年第四届数学文化征文活动

我从事数学科普写作的经验与启示

作者：巢洪政

作品编号：020

笔者1986年中师毕业，走上了小学数学教师的工作岗位。因为上学时比较喜欢写作，故从1988年起，我就开始撰写和发表小学生数学学习科普文章，至今已有30余年。从第一篇发表的文章算起，至今已经发表了此类文章近三百篇。

笔者认为，凡是能够有益于小学生数学知识的学习，对他们的数学学习起到帮助辅导作用的，或者能够促进学生数学阅读，有益于传播数学文化，对孩子们学好数学有一定启示作用的文章，均可通称为小学数学学习科普文章，例如：有关知识介绍、概念辨析、错误纠正、习题解析、故事童话、专题辅导、专题练习，甚至是数学相声、笑话和幽默等内容都是数学科普文章的内容，此类文章也可以称为数学学习辅导文章。

经过长期的写作实践和总结发现，我一般经常写作以下五类数学学习科普文章，用来指导学生学好数学知识，激发他们数学学习的兴趣，培养他们的数学学习能力。下面总结出它们的主要撰写要点，并列举例子，为老师们撰写和分析此类文章起到肤浅的借鉴作用。

一、知识辅导文章。专门撰写与小学数学教材关系密切的知识辅导文章，这样的文章，要紧扣小学数学教材的内容进行写作，做到既源于教材，又略高于教材，能够做到帮助学生既深刻理解数学教材上的有关知识，又能够通过此类文章课外的阅读，使他们学到的数学知识得到进一步的提升。这样的文章，能够有效地帮助小学生深入理解教材内容，准确地理解数学概念，灵活地学会解题技巧，多角度地找到数学问题的解法，从而拓展他们的数学思维。例如：为了指导六年级学生学好有关“倒数”的知识，我撰写了下面的科普文章：

学好倒数知识“三要”

同学们已经知道：乘积是1的两个数互为倒数。我们在学习和理解倒数的知识时，要注意做到以下三点：

1.要理解意义正确叙述。

倒数是指两个数之间的一种关系，这样的两个数可以是分数，也可以是小数和整数，只要它们的乘积是1，这两个数就是互为倒数的数，因此，我们在叙述成倒数关系的两个数时，应该说出两个数之间的相互依存关系，不能单独说某个数是倒数。如：，我们就可以说：是2.5的倒数；2.5是的倒数；和2.5互为倒数；但不能说：、2.5是倒数；是倒数；2.5是倒数。还有需要我们明确的是：因为1×1=1，所以1的倒数是1本身；由于没有数和0相乘得1，因此0没有倒数。

2.要正确求出各种数的倒数。

求一个数（0除外）的倒数的方法是：把这个数（真分数和假分数）的分子、分母调换位置。如，的倒数是；的倒数是。对于其他各种数的情况，我们应该按照这样的基本方法灵活求出倒数。

①一个自然数的倒数，就是将这个自然数作分母，分子是1的分数。如：9的倒数是；21的倒数是。

②一个带分数的倒数，就是要将带分数先改写成假分数，再求出倒数。如，的倒数应该这样求：因为，所以，的倒数是。

③一个小数的倒数，应该先将小数化成分数，特别是最后带分数的要化成假分数，然后求出这个分数的倒数。如：2.6的倒数应该这样求：因为,所以，2.6的倒数是。

3.要能够利用倒数的知识解决问题。

在掌握了倒数的有关知识后，我们还可以利用这个知识解决一些数学问题。如：你能用倒数的知识来填吗？

3×＝× ＝ ×＝×。

解答这个问题，我们可以用最简单的方法分析，即假设这些算式的结果都是1，那么算式中相应的两个因数就互为倒数了，显然，里从左向右依次可以填：、4、、；如果假定这些算式得数是2、3、……，也可以求出答案，但比较麻烦。当然，如果将等式里的四个分别换成字母a、b、c、d，需要比较它们的大小，也是可以这样分析的。

再如：用倒数的知识来比较和的大小。可以这样思考：由于这两个数的倒数分别是：和，所以，，，显然是，因此，；而对于它们原来的数来说，应该是：。

最后，留给同学们一个思考题：有三个素数的倒数和是，这三个素数分别是多少？你能用倒数的知识找出答案吗？

二、习题解析文章。此类文章专门撰写的是各种与小学数学教材关系密切的、又对教材中的数学知识有提升作用的各类习题分析与解答的文章，这样的文章，是通过对某个知识点范围内的典型习题进行详细的解析，以帮助学生掌握某类问题的解题方法，提高解题能力，拓展他们的解题思路。此类文章较多的是多、针对教材中的思考题或者是常见题的剖析，尤其注意尽量做到帮助学生掌握一题多解的方法，拓展学生的解题思路。例如：在五年级同学学习了多边形面积的计算后，我撰写了下面的文章，帮助他们掌握多种方法计算多边形的面积。

思考 解答 比较

问题：图(1)是一个平行四边形，面积是28平方厘米，求阴影部分的面积。

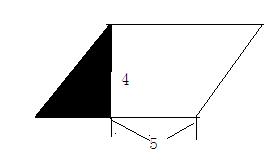
图1

解法一：先求出平行四边形的底，然后求出阴影部分三角形的底，最后求出阴影部分的面积。列式解答是：

(28÷4－5)×4÷2=2×4÷2＝4(平方厘米)。

答：阴影部分的面积是4平方厘米。

解法二：先求出平行四边形的底(也就是空白部分梯形的上底)，然后求出梯形的面积，最后再用平行四边形的面积减去梯形的面积得到阴影部分的面积。列式解答是：

28－(28÷4 5)×4÷2

=28－12×4÷2

28－24＝4(平方厘米)。

答：阴影部分的面积是4平方厘米。

解法三：先添一条辅助线(如图(2))，求出中间长方形的面积，然后用平行四边形的面积减去长方形的面积，得到两个三角形的面积，最后除以2求得阴影部分的面积。

列式解答是：

(28－5×4)÷2=8÷2＝4(平方厘米)。

答：阴影部分的面积是4平方厘米。

请同学们想一想，这道题还有其它解法吗?比较一下，上面三种解法中，哪种解法好。

三、趣味数学作品。此类作品专门撰写的是与数学有密切联系的趣味性较强的文章，能引导学生体味数学知识应用的广泛性，领略数学知识中的趣味性，让学生读来非常有趣，读完后又很有收获和启发。例如：为了帮助高年级的孩子们更好地理解数学中的“统筹兼顾”的思想方法，我撰写了这样一篇趣味数学的文章：

运用数学 统筹兼顾

完成一件事情怎样合理安排才能做到用时最少，效果最好。在解决这样的问题时，我们往往要综合考虑各方面的因素，统筹思考才能得出答案，这样解决问题的思想方法在数学中称为统筹思想方法。统筹思想方法是一种合理安排工作进程的数学思想方法。它的使用范围在生产、生活中比较广泛，尤其在企业管理和基本建设，以及关系复杂的科研项目的组织与管理中，经常需要应用。

解决这类问题时，关键是必须树立统筹兼顾思想，做到能同时做的事，尽量同时做；让大家等待时间最少的事，可以首先做。

比如，你想泡壶茶喝。当时的情况是：开水没有；水壶要洗，茶壶茶杯要洗；火生了，茶叶也有了。怎么办？

最省时间的办法是：洗好水壶，灌上凉水，放在火上烧开水；在等待水开的时间里，洗茶壶、洗茶杯、拿茶叶；等水开了，就可以泡茶喝了。

这是日常生活中的小事，但这是引子，根据这样的思想可以类似地引出生产管理等方面的很有用的方法来。我国宋代有位宰相丁谓就运用统筹思想方法的原理，解决了一个非常复杂的问题。

宋朝真宗时期，皇宫失火，烧毁了不少宫殿，真宗皇帝十分恼火，下令必须在三个月内重新修复皇宫。要修复皇宫，还要大修道观，整个工程十分浩大。宰相丁谓负责了这项建筑工程。他努力想要做到既迎合皇帝求仙的需要，又要不加重了人民负担，实在是伤透了脑筋。但经过丁谓的精密筹划，工程取得了令时人赞叹不已的成功。

丁谓为人机敏多谋，琴棋书画无不精通。他想贸然动工难免劳民伤财，要在短时期内修复大批宫殿决非易事，首先，修筑宫殿需要大量泥土，但皇宫中没有这么多土，得从数里外的城郊去运土。其次，各地从水路运到开封的建筑材料无法靠船筏直接运入宫中，要把这些东西从城外运到工地还得花大量人工。再次，要把烧毁的砖瓦和建筑垃圾运出城外，也不是件容易的事。

丁谓冥思苦想，终于设计出一个完美的施工方案。他先让民工在皇宫前面的大路上开挖泥土，将取出的泥土运入工地。没几天大路便被挖成了一条宽阔的深沟，这样就备足了修复宫殿所需要的泥土。然后，他下令把深沟和城外的大河挖通，将河水引入深沟，深沟就成了河道。这一来，停泊在域外的船筏就可以径直驶到皇宫门口。再把上面的建筑材料运到工地就方便多了。宫殿修复完毕后，丁谓又吩咐民工将建筑垃圾填入深沟，没过多久，深沟又被修整成一条宽阔的大道。

丁谓的施工方案省时省力，巧妙地运用了统筹兼顾的思想方法，妥善地解决了取土、运输和处理建筑垃圾等问题，按时完成了任务，真可谓一举而多得。

生活中很多问题都可以用这种统筹的方法解决，同学们可以在生活中找一找。

四、专题辅导文章。此类文章是为了帮助学生拓展数学知识，围绕某个数学知识点编写的专题数学科普辅导文章。这样的文章，能够有效地帮助孩子们巩固某方面的数学知识，有效地帮助他们拓展数学知识，开拓解题的视野，有时涉足部分奥数的知识，能够较好地提高数学思维能力较强的孩子的解题能力。一般在此类文章的最后，需要帮助学生总结这个专题数学问题的解答要点或方法，并配有一定数量的相关练习。例如：在学过“倍数和因数”的有关知识后，我撰写了利用质因数的知识解决实际问题的专题辅导文章，较好地帮助学生体会到“质因数”的知识在实际生活中的广泛作用。

巧用质因数解决问题

把一个合数用若干个素数（质数）的因数相乘的形式表示出来，叫分解质因数。如：20=2×2×5、30=2×3×5；在分解质因数时同学们要注意：分解出的因数中不能有合数和1，一般要把质因数按从小到大的顺序排列起来。运用分解质因数的知识，能够帮助我们解决一些问题。

问题1：红光小学有1430名同学参加团体操，分成人数相等的若干队，每队的人数在100到200人之间，可以有几种不同的分法？

思路点睛：由于每队的人数是相等的，因此，每队的人数乘以队数等于一共的人数1430人。显然，每队的人数和分成的队数都是1430的因数。把1430分解质因数得：1430=2×5×11×13。考虑到每队的人数在100到200人之间，我们应该在1430的四个质因数2、5、11、13中选若干个因数相乘，使它们的乘积在100到200之间，于是我们可以得到三种不同的答案：（1）2×5×11=110，（2）2×5×13=130，（3）11×13=143。所以，这个问题的答案是：每队的人数是110人、130人或143人，可以有3种不同的分法。

问题2：将26、39、46、57、85、95、119、161这八个数分成两组，使每组四个数的乘积相等，应该怎样分？

思路点睛：要将这八个数分成两组，每组中的四个数乘积相等，只要使这两组数中都有相同的质因数就行了。因此，我们可以先把这八个数分解质因数，然后把相同的质因数分摊在两组中，使每组中含有相同的质因数。即：26=2×13，39=3×13，46=2×23，57=3×19，85=5×17，95=5×19，119=7×17，161=7×23。这八个数的所有质因数中，共有2个2、2个3、2个5、2个7、2个13、2个17、2个19、2个23。把它们平均分摊即可。分成的两组数是：26、57、85、161和39、46、95、119。

问题3：小明和小刚到公园的打靶场练习射击。靶上依次标明1、2、3、4、5、6、7、8、9、10环和0环（没有打中靶）。他们两人各自打了5枪，打出的5个环数之积正巧都是2520。他们两人的射击成绩最多相差多少环？

思路点睛：要想知道两人的射击成绩最多相差多少环，我们就要先确定两人射击5枪的环数之和可能得到的最大和最小值分别是多少环。先将2520分解质因数是：2520=2×2×2×3×3×5×7。由于两人每次的成绩都是不超过10的整数，这里同学们要注意考虑到某次的成绩还可能是1环，但因为5个数的积是2520故不可能是0环。这样将2520的7个质因数和1进行组合，得到所有可能的情况是：（1）3×4×5×6×7，即3＋4＋5＋6＋7=25；（2）2×4×9×5×7，即2＋4＋9＋5＋7=27；（3）1×5×7×8×9，即1＋5＋7＋8＋9=30；（4）2×5×6×6×7，即2＋5＋6＋6＋7=26；（5）1×4×7×9×10，即1＋4＋7＋9＋10=31；（6）3×3×8×5×7，即3＋3＋8＋5＋7=26；（7）2×3×6×7×10，即2＋3＋6＋7＋10=28。经过比较可以看出，最大的和是31，最小的和是25。因此，这个问题的答案是：两人成绩最高是1、4、7、9、10环，最低是3、4、5、6、7环，射击的成绩最多相差31－25=6（环）。

总结与提示：根据分解质因数的知识解决有关的问题，首先要根据题意将问题中是若干个数的乘积的一个或几个数量所相应的数分解质因数，然后根据分解质因数得到的各个因数的情况，进行合理的组合，有时还要考虑1和0的特殊作用，推算出符合题意的全部答案，使问题得以顺利解决。

每日思维操：

星期一 儿童的年龄

有五个儿童的年龄和是34岁，积为9240，如果每个儿童的年龄都不超过13岁，这五个儿童的年龄各是多少岁？

星期二 成绩和名次

上初中的丁丁是个数学谜，去年他参加了全市的数学竞赛。竞赛结果揭晓后，他的同学问他：“这次数学竞赛你得了多少分？获得第几名？”丁丁说：“我的名次、我的岁数和我的分数连乘的积是2910，你能猜出我的成绩和名次各是多少吗？”

星期三 分组

把20、26、33、35、39、42、44、55、91这九个数分成三组，使每组三个数相乘的积相等。

星期四 买画片

聪聪用2.16元买了同一种画片若干张，如果每张画片便宜1分钱，那么他还能够多买3张画片。聪聪买了多少张画片？原来每张画片多少钱？

星期五 射箭

在射箭训练中，东东和平平两人每射一箭得到的环数都是2至10中的一个自然数。他们各射了5箭，每人射中的环数的积都是1764，但东东的总环数比平平少3环，东东和平平两人各自共射中了多少环？

五、故事童话作品。此类文章，主要是撰写与数学有关的故事或童话作品，把一些学生难以理解的数学知识与故事、童话等儿童文学形式有机结合，做到每篇作品中都隐含着至少一个数学问题，内容生动贴切，充满童趣，学生读来既喜欢愉悦，又能够通过思考掌握一定的数学知识，获得一些有益的启示，进行必要的道德教育，并能够切实让孩子们体会到数学与社会生活的密切联系。例如：为了对孩子们进行合理分配、防骗教育和诚信教育，我撰写了这样一则童话：

分钱

愉快的暑假生活开始了，可乐坏了大花猫和灰狐理。这天，他俩结伴去游乐园玩。游乐园可真有意思，大花猫和灰狐狸在里面玩荡秋千、碰碰车、开水上飞机……可开心了，几乎忘记了时间。

很快就到了中午，他们俩来到路边的大树下准备吃午饭，大花猫拿出自己带来的8张饼，灰狐狸也拿出带来的7张同样的饼。这时，一只金丝猴匆匆忙忙地走过来，对大花猫和灰狐狸恳切地说:＂两位朋友，帮帮忙！我今天早晨走得匆忙，忘记了带午饭，现在饿得我眼冒金星，请把你们的饼分给我一些吧，我付钱给你们。＂看着金丝猴可怜的样子，大花猫和灰狸都点头同意了，他们把带来的饼平均分成三份，给了金丝猴一份。金丝猴拿起饼就大口大口地吃了起来，很快就吃完了，向大花猫和灰狐狸道了谢，拿出4.5元钱留给了灰狐狸，便匆匆地离开了。

灰狐狸拿着金丝猴留下的钱，眼珠一转计上心来。趁着大花猫还没仔细想，便说道:“我们俩共拿出15张饼，金丝猴给我们4.5元钱，那平均每张饼的价钱就是4.5÷15＝0.3(元)；这样，我分得0.3×7＝2.1(元)，你分得0.3×8＝2.4(元)，对不?”大花猫听了灰狐狸的话，觉得有点道理，刚要和灰狐狸分钱，可它仔细一想，又觉得不对。因为一共有15张饼，平均每人分了5张饼，金丝猴付的4.5元钱是他吃的5张饼的钱，因此，每张饼的价钱应该是4.5÷5＝0.9(元)。这样，自己拿出3(8-5)张饼，应分得0.9×3＝2.7(元)，灰狐理拿出2(7-5)张饼，应分得0.9×2＝1.8(元)。想到这，大花猫便对灰狐理说:“狐狸老兄，赖朋友的钱，怪难为情的吧?＂

灰狐理知道自己的诡计被大花猫识破了，羞得满脸通红，拿着自己应该分得的钱，灰溜溜地先走了。

原来，由于一共15张饼，平均每个分得5张饼，4.5元钱是金丝猴付自己吃的5张饼的钱，因此，每张饼的价钱是：4.5÷5=0.9（元）；这样大花猫拿出3（8-5）张饼，应收0.9×3=2.7（元），灰狐狸拿出2(7-5）张饼，应收0.9×2=1.8（元）。

因此，灰狐狸是想冒领大花猫的钱呀！

另外，我还结合自己对数学单元知识的理解，撰写了许多学生单元练习题或者是期末练习题，在有关报纸上得以发表。平时，还非常重视指导数学成绩优秀的学生撰写数学小论文，已经有数十位学生的数学小论文在各类报刊上发表，大大地激发了他们学好数学的积极性，当孩子们看到自己的小论文在有关报刊发表，事后还收到了一定的稿费，这样的成功喜悦是无法用语言来表达的，当然，这样的情况一定会在他们的记忆中留下深深的回忆，也更加能够激发他们学好数学的热情。

三十多年的数学科普文章写作的实践，让我从一名毫无经验的数学青年教师，成长为一名资深的小学数学教师，取得了一定的知名度，并在教学和科研方面都获得了丰硕的成果。早在1992年暑假，本人就作为南京的小学生数学报的骨干作者，应邀参加座谈会，有幸与我国数学科普名家李毓佩、谈祥柏和许多国内的小学数学名师一起相识。在写作数学科普文章的同时，通过不断地学习，我的教研水平不断得到提升，对数学教材的理解日益深入，文字表达水平不断提升，还帮助我在数学教育科研的道路上取得了优秀的成绩。至今已经有五十余篇教育论文在省级以上教育刊物发表或被人大报刊复印资料全文转载，本人主持的江苏省重点立项课题成功结题，撰写的教育论文在全国、省或市级评比中获奖数十次，曾经三次作为特邀代表应邀参加省小学数学教学研讨会，并作大会经验交流；应邀参加十多本教师用书或学生学习辅导用书的编写或修改工作。并先后被评为江阴市“百佳书香教师”和省小学数学教学网“优秀网友”。我指导的学生中，有十多位获得省市各类数学比赛的奖项。这些成绩的取得，都首先归功于我撰写数学科普文章后打下了良好基础。

我从事数学科普写作的经历还使我深深地体会到，做教育研究工作也要根据自身的实际情况，从小事做起，扎扎实实一步一个脚印，日积月累地不断努力，才能取得一定的成绩。一段时间内，据李毓佩教授介绍，在国内数学教育界的有些人看不起学生科普文章的写作工作，错误地认为这项工作是低水平的工作，不值得大家一做。而实际的情况是，即使是像华罗庚等许多这样的大数学家，也是曾经写过大量的数学科普文章的，这对引导后辈步入数学研究的殿堂，指导公众提高数学素养，都是非常重要的工作。作为一名数学老师，应该自觉地担当起这方面的责任，为更加广泛地传播数学文化，丰富孩子们的数学阅读内容进行认真的研究和创作，无论是对学生还是对作者本身，都是很有收获的好事。

总之，作为一名优秀的数学老师，能够做到经常阅读和撰写数学科普文章，并注意引导和鼓励学生阅读数学科普文章，学写数学小论文，既能够对自己的专业发展和教育科研工作有巨大的促进作用，也能够为孩子们的数学阅读和数学文化水平的提升起到引领和促进作用，是一件值得大家重视的功德无量的大好事！

已发文章>>

001 阅读《数学的故事》有感

002 我想和数学谈场恋爱

003 数学“化错”中的美

004 让数学思考成为数学课堂的主旋律

005 卢梭的“错”？

006 数学教学案例《找次品》

007 基于优化学生数学思维的高效课堂创建——以等腰三角形的判定一课为例

008 从特殊到一般，引导数学思维

009 数学文化融入家庭教育的研究

010 sin 震荡函数的图像分析

011 四阶幻方的“太极图”性质

012 无理数的定义和实数理论的建立

013 一个容易被忽视的问题——数学文化

014 “双减”背景下初中数学学科的合作学习方式探究

015 中学数学德育渗透的方法与路径

016 《数学的力量》读后感

017 基于数学文化的单元统整教学设计——以“圆的认识与面积”教学为例

018 有助于数的理解的数字圈环

019 以折叠为例，探究生长型数学教学模式

,