用平面向量证明立体几何（证明立体几何垂直关系第五招一一向量法）

万物皆数，用数表示世界，通过数的计算解决问题是数学的一大特点与进步，向量就是数与形最好的结合。

例题：如图所示，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=PB=PC=2CD，侧面PBC⊥底面ABCD，证明：PA⊥BD。

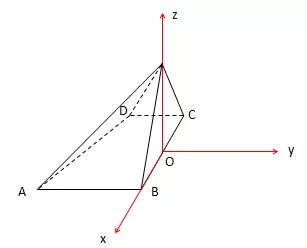
证明：

取BC得中点O，连结PO，

∵平面PBC⊥底面ABCD，△PBC为等边三角形

∴PO⊥底面ABCD

以BC的中点O为坐标原点，以BC所在直线为x轴，过点O与AB平行的直线为y轴，OP所在直线为z轴，建立空间直角坐标系如下：

变式：如图，正三棱柱ABC-A1B1C1的所有棱长都是2，D是CC1的中点，求证：AB1⊥面A1BD