中考数学特殊三角形总结（三角形重不重要）

新学期即将开学，对于所有中小学生来说，又要开启新的征途。新学期新气象，除了要掌握好已学的知识定理和方法技巧，更要从容面对新学年带来的新变化。特别是对于初三新生来说，这种变化会更加明显，如题目综合性变强，难度越来越大，解法变得更加灵活等。

如三角形的学习，在初一初二期间，我们接触的题型都是较为常见，难度并不是很大，但进入初三之后，一些以三角形为知识背景设计的题型，难度和综合性就上了一个新的层次。

三角形有关的知识内容一直是中考数学必考的热点内容之一，无论时全国哪个地方的中考试卷，必定都会考到三角形，这点大家一定要清清楚楚。

如对三角形三边关系、三角形内角和定理、勾股定理及其逆定理等知识的考查，通常以选择题、填空题何解答题的形式出现，题型丰富；其中全等三角形的性质和判定、等腰三角形的性质和判定、直角三角形的性质等知识仍然是考查的重点，它通常和其他知识结合在一起，以解答题的形式出现，所占分值较高。

​三角形有关的中考试题，典型例题分析1：

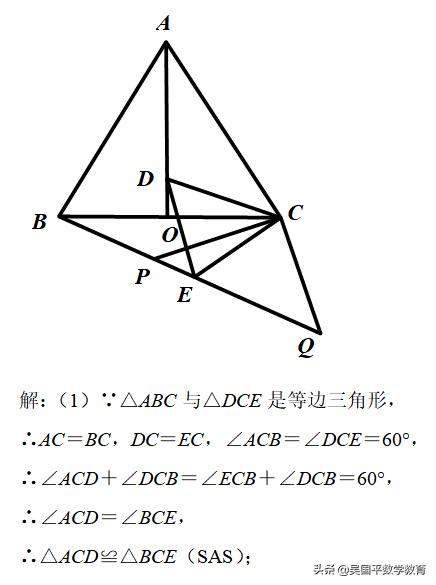
如图，等边△ABC中，AO是∠BAC的角平分线，D为AO上一点，以CD为一边且在CD下方作等边△CDE，连接BE．

（1）求证：△ACD≌△BCE；

（2）延长BE至Q，P为BQ上一点，连接CP、CQ使CP＝CQ＝5，若BC＝8时，求PQ的长．

​

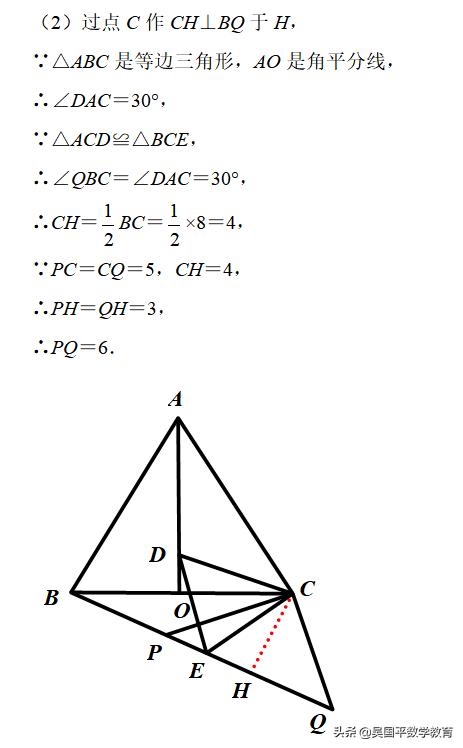
​考点分析：

全等三角形的判定与性质；等边三角形的性质；含30度角的直角三角形；勾股定理；几何综合题。

题干分析：

（1）由△ABC与△DCE是等边三角形，可得AC＝BC，DC＝EC，∠ACB＝∠DCE＝60°，又由∠ACD＋∠DCB＝∠ECB＋∠DCB＝60°，即可证得∠ACD＝∠BCE，所以根据SAS即可证得△ACD≌△BCE；

（2）首先过点C作CH⊥BQ于H，由等边三角形的性质，即可求得∠DAC＝30°，则根据等腰三角形与直角三角形中的勾股定理即可求得PQ的长．

解题反思：

此题考查了全等三角形的判定与性质，等腰三角形、等边三角形以及直角三角形的性质等知识．此题综合性较强，但难度不大，解题时要注意数形结合思想的应用．

​三角形有关的中考试题，典型例题分析2：

如图，抛物线y=ax² bx（a＞0）与双曲线y=k/x相交于点A，B．已知点B的坐标为（﹣2，﹣2），点A在第一象限内，且tan∠AOx=4．过点A作直线AC∥x轴，交抛物线于另一点C．

（1）求双曲线和抛物线的解析式；

（2）计算△ABC的面积；

（3）在抛物线上是否存在点D，使△ABD的面积等于△ABC的面积．若存在，请你写出点D的坐标；若不存在，请你说明理由．

​

​

​考点分析：

二次函数综合题；代数几何综合题。

题干分析：

（1）根据已知条件可以推出A点的坐标，把A、B两点的坐标代入抛物线解析式和双曲线解析式，即可得出a、b、k的值，就可以确定双曲线和抛物线的解析式了；

（2）根据A、B抛物线解析式，可以确定C点的坐标，即可去顶AC和AC边上的高的长度，就可以计算出△ABC的面积了；

（3）根据题意画出图形，根据A、B两点坐标出去直线AB相应的一次函数结合C点的坐标，CD∥AB，得出直线CD相应的一次函数，然后结合D点也在抛物线上，解方程组，求D点坐标

解题反思：

本题是二次函数的综合题型，其中涉及的到大知识点根据点的坐标求抛物线解析式和双曲线解析式以及三角形的面积求法．关键在于根据点的坐标和相关的知识点求抛物线解析式，曲线解析式和直线解析式．

​​三角形有关的中考试题，典型例题分析3：

在梯形OABC中，CB∥OA，∠AOC=60°，∠OAB=90°，OC=2，BC=4，以点O为原点，OA所在的直线为x轴，建立平面直角坐标系，另有一边长为2的等边△DEF，DE在x轴上（如图（1）），如果让△DEF以每秒1个单位的速度向左作匀速直线运动，开始时点D与点A重合，当点D到达坐标原点时运动停止．

（1）设△DEF运动时间为t，△DEF与梯形OABC重叠部分的面积为S，求S关于t的函数关系式．

（2）探究：在△DEF运动过程中，如果射线DF交经过O、C、B三点的抛物线于点G，是否存在这样的时刻t，使得△OAG的面积与梯形OABC的面积相等？若存在，求出t的值；若不存在，请说明理由．

​

​考点分析：

二次函数综合题。

题干分析：

（1）根据F与B重合前后及E与A重合前后，分三种情况求S关于t的函数关系式；

（2）依题意得D（4﹣t，0），求出直线OC解析式，根据DF∥OC确定直线DF解析式，再由△OAG的面积与梯形OABC的面积相等，求出G点纵坐标，根据G点在抛物线上求G点横坐标，代入直线DF解析式求t，判断是否符号t的取值范围即可．

解题反思：

本题考查了二次函数的综合运用．关键是根据直角梯形的特点求顶点坐标，确定抛物线解析式，根据面积关系，列方程求解．

三角形作为初中数学的重点内容之一，也是各地中考命题的必考知识，希望所有初三生在平时学习过程中，要认真对待。

,