量子力学的内在不确定性（如何理解量子力学中的不确定性原理）

这是一篇

硬核文章

喜欢生活大爆炸，因为喜欢外星人一样的Dr. Sheldor Cooper。各种强迫症，各种折腾人，还各种秀智商，除了剧里的人受不了，恐怕没有观众不爱他了吧。最近，只想做一条咸鱼的我又开始看Sheldor藐视同伴的智商了。

Sheldor的笑话（S10E21）

上面是我最近看到的Sheldor同志讲的一个笑话，看完后当时我就震惊了，what the hell? 这居然是个笑话？可我连他在说什么都不知道啊。原来Sheldor不只是在藐视同伴的智商，也同时在告诉我自己有多失败。不过，好奇的我还是去百度了一下，明白这里的笑话是以海森堡的不确定性原理为基础的，该理论是说，粒子的位置与速度不可同时被确定，而Sheldor在笑话中把海森堡比作了粒子。

不确定性原理

沃纳·卡尔·海森堡

不确定性原理由德国物理学家海森堡于1927年提出，是量子力学的重要概念之一。该原理表明，精确确定一个粒子（例如原子核周围电子）的位置和动量（速度）是不可能的，位置的不确定程度越小，则动量的不确定程度越大，反之亦然，用公式表示为

其中

表示粒子位置的不确定程度，

表示粒子动量的不确定程度，h表示普朗克常数，这个数很小很小，约等于

。

从上面公式中可以看到，如果我们完全确定了粒子的位置，也就是说

，那么要想满足上面的不等式，只能让

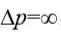
，此时粒子的动量（速度）可以是任意值（完全不确定），反之亦然。当然我们也可以降低标准，让位置和速度的测量都不那么精确，此时两个量同时不确定。

我们知道，在宏观中，同时确定一个物体的位置和速度是很容易的（考试题目除外），为什么会在微观世界中存在这么反直觉的现象呢？这还要从粒子的波粒二象性说起。

波粒二象性

波粒二象性说的是，一切物质都具有波粒二象性，物质在某些情况下会表现出粒子的性质，但在某些情况下会表现出波的性质。德布罗意给出了物质动量p的计算公式

其中l表示物质的波长。目前来看，宏观物体还没有表现出波动性，这里仅仅讨论微观粒子。

从这个公式我们可以得到一条重要信息，就是粒子的动量和波长呈反比关系。二者之间的直接联系表明，动量大小体现了粒子的波动性。而粒子的位置描述的显然是其粒子性。我们知道，粒子和波是相互矛盾的两个对象，我们无法准确描述一个波的位置，也无法准确描述一个粒子的波长，不确定性原理正是二者矛盾性的一种体现。

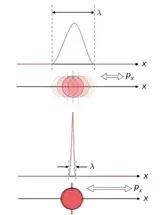
波与粒子的矛盾

应该说，上面的解释可以作为不确定性原理的定性理解方式。想要从最严格的角度解释不确定性原理，我们还需要适当引入一些量子力学的基础知识。

不确定性原理的精确解释

开始之前先说一下，量子力学和其它很多学科的不同的地方就在于，它会给所有东西都起一个很高大上的名字，让身处物理世界之外的同学望而生畏。比如说，粒子的状态可以用波函数来描述，一般记为

（其实用y表示也不是不行，但是就显得有点太low了）。我们可以通过操作波函数获得粒子的能量、动量、位置等等所有物理量的信息。操作手段很多，比如说可以对波函数求导，给波函数乘以一个数，等等。不同的操作手段可以得到不同的物理量信息，量子力学也给这些手段起了个很高大上的名字，叫算符。

下面单独考虑一下位置算符和动量算符，其中位置算符

，而动量算符

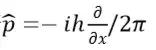
（这里不用管为什么，直接把物理学家给出的结果拿来用一下就行），对任意一个波函数

，考察下面这个积分

这里的*表示一个数的复共轭，

是任意复数，

表示位置的平均值，

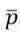
表示动量的平均值，显然该式子是大于0的。整理一下可以得到

值得注意的是，位置的不确定程度

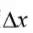
和动量的不确定程度

分别满足

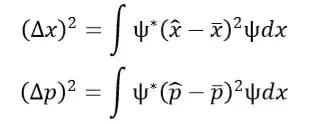
再令

(这里使用了位置算符和动量算符的表达式，并代入了得到的

，取

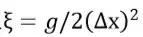
，则有

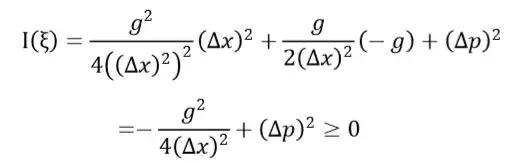
这样就得到了海森堡的不确定性原理

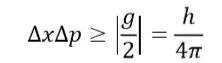
上面的式子展示了不确定性原理产生的根源，即

，也就是

，或者

，量子力学对这种现象也起了个很高端的名字，称两个算符不对易。如果两个算符交换位置后的乘积相等，就称这两个算符对易。那么，结论就很清晰了，不确定性原理的出现就是由位置算符和动量算符不对易造成的。

如何理解

这种奇怪现象呢？我们借用一些其他事物来类比一下。学过线性代数的同学都知道，对于两个矩阵A和B，AB和BA的值不一定相等，算符和矩阵有着相同的性质。再比如说，我喜欢一个妹子，但是反过来，妹子不喜欢我，那么我们之间的关系也是不对易的。

好了，有了不对易的概念之后，我们只剩下最后一个问题，为什么算符的不对易会导致不确定性原理呢？

先说一下波函数，它表示了粒子的状态，在每种状态下，粒子的速度和位置都存在一个概率分布。但有一些状态是比较特殊的，这些状态叫本征态，如果是位置的本征态，那么粒子的位置就完全确定，反之，如果是动量的本征态，那么粒子的动量就完全确定。所以说，如果粒子的位置和动量具有相同本征态，那么粒子的位置和动量就可以同时确定，而位置算符和动量算符不对易造成了它们没有共同本征态。

对于对易算符而言，二者仿佛心有灵犀，只用用心去寻找，就能找到共同本征态，就像是如果你和女神相互喜欢，只要你们去努力，总能找到自己的共同本征态。然而，现实很残酷，往往是我喜欢女神，但女神却对我毫无感觉，无论多么努力，两个人之间总是存在隔阂。很不幸，位置和动量就是这样的一对冤家，所以它们两个也就永远不能同时被确定了。

不确定性原理的另一种解释

另外，也有一些解释认为，不确定性原理是由于测试手段的限制造成的。比如说使用光照到一个粒子上的方式来测量一个粒子的位置和速度，为了精确测定粒子位置，必须用短波长的光，但波长太短则意味着光的能量越大，对粒子的扰动也就越大，对粒子动量的测量也就越不精确；如果想要精确测量粒子的动量，那就要用波长较长的波，那么就不能精确测定粒子的位置。

这里需要说明的是，本人认为该解释并非导致不确定性原理的真正因素，其真正来源仍然应该是算符不对易。

最后讲几个和不确定性原理相关的笑话结束全文：

1. 费曼说他一直无法理解非对易性，直到有一天，他在夜店尝试过一些新鲜的动作之后，终于领悟到AB≠BA。

2. Q: Why is the particle physicist bad lover?

A: Because when they find the momentum, they can’t find the position. Whenthey find the position, they can’t find the momentum.

,