自然常数e是怎么被定义的（Emc²质能方程中为什么会出现光速平方呢）

E=mc²，史上最出名的物理公式之一，揭示了物体所含能量与其自身质量的本质关联，如果说爱因斯坦和相对论之所以有这么大名声，这个公式的贡献得占一半。

名声大归名声大，有些朋友在仔细思考这个公式后有了这样的疑惑：

质能方程揭示了能量与质量的关系，可为什么在公式中的系数一定要是光速的平方呢？我知道光速是一个常数，但为什么非要平方，而不是什么立方之类的呢？

实际上这样的疑惑并没有什么价值，甚至可以说是无用的，为什么这么说呢？很简单，如果你采用几何单位制，那么质能方程就直接变成了E=m，光速c连个影子都没有出现，因为在几何单位制中，光速c的值为1，利用这种单位制，使得质能方程的含义更加一目了然。

可能有些朋友又要反驳了，你转化单位制只是取巧而已，从国际单位制到几何单位制，虽然样子变了，但少掉的光速只是化作另一种形式埋藏在公式里，而现在我只想知道为什么质能方程会出现光速，为什么在国际单位制中还是以光速平方出现的？

既然如此，那么只能用狭义相对论去解释了，因为质能方程本身就是狭义相对论的推论之一，而光速这一物理量在狭义相对论中具有特殊地位，因为建立狭义相对论的两大基础之一就是光速不变原理。如此说来，如果要讲的一清二楚，那我们相当于要讲狭义相对论从头开始推导才行，然而这显然不适合在科普文章中出现，因此我们必须先找一个共同承认的认知基础，然后在此基础上进行推导，这样既不失严谨，也不会显的过于繁杂。

那么这个共同的认知基础是什么呢？没错，就是狭义相对论的质增效应，也就是我们平常所说的物体运动速度越快，其质量就变的越大（当然了，这样的表述纯粹是为了科普而言，不过我们也没必要纠结，大概意思对即可）。

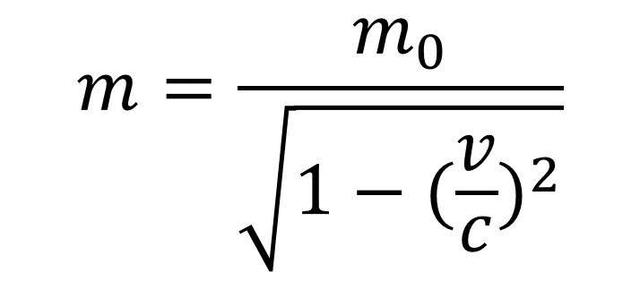
首先，我们得先承认质增效应是存在的，合理的，那么在此基础上我们对一个运动物体的动能进行推导，物体由静止出发，利用动能是力与位移的乘积这一点，具体过程如下图所示：

其中我们注意到，力在狭义相对论中的定义仍旧是动量对时间的求导，但这里的动量不同于牛顿力学中的动量，因为质量不再是一个定量，而是变量（也就是质增效应的表现），在注意到这点之后，接下来的就是常规的数学推导了，最后得到了一个这样的公式：物体动能=mc²-m0c²，其中m0代表物体静止时的质量，m代表运动时的质量。

对于这样的结论，我们首先会发现物体的动能公式变了，牛顿力学中是1/2mv²，而狭义相对论中则完全变样了，不过在低速情况下，狭义相对论中的动能公式仍可以退化为牛顿力学形式；此外爱因斯坦还将mc²假设为物体运动时的总能量，m0c²称之为静止时的能量，至此质能方程就出现了。

当然了，最初爱因斯坦推导质能方程时并不是用的这个方法，而是利用一个发光体位于不同惯性系下的表现从而得出结论，下图就是当年爱因斯坦提出质能方程的论文《物体的惯性是否取决于它的能量含量？》

如果单看这篇论文的话，有一些条件是看不懂的，因为这篇论文的内容实际上是承接的《论动体的电动力学》（也就是后来被称为狭义相对论的那篇论文），可以说是一篇补充性论文，但就是这篇简短的补充性论文，却提出了后来广为流传的质能方程。

现在就可以回答题目中的问题了，质能方程中为什么会出现光速，为什么又恰恰是光速的平方？因为这是数学推导的结果，追根溯源的话，那就是狭义相对论的两个基础——“光速不变原理”和“狭义相对性原理”，你对质能方程的一切疑惑和质疑，全部都来自你对“光速不变原理”和“狭义相对性原理”的不理解（尤其是光速不变原理）。

退一步来讲，对光速不变原理产生疑惑，实际上也是正常的，因为从常识的角度考虑，光速怎么可能会不叠加呢？因为日常生活中运动物体的速度都是可以叠加的啊。但遗憾的是，不论从麦克斯韦方程还是迈克尔逊莫雷实验，光速在任意惯性系下都是一个定值，已经成为了我们不可争辩的事实。

与其反对它，不如尝试接受它，一旦以这样的结论作为先提条件，我们会发现由此诞生的狭义相对论，为自然界中更多的物理现象提供了更好更合理的解释，比如人类后来研究出的核武器，质能方程就是解释了为什么核武器能够有如此巨大的能量释放（注意一点，质能方程并不是核武器研制的理论基础，仅仅是解释了巨大能量的来源）。

总的来讲，我们不必纠结为什么是光速的平方，因为E=mc²是狭义相对论的一个很自然的推论，理论所反映的只是宇宙的一组自然规律罢了，至于为什么规律是这般模样，这是一个科学无法回答的问题。因为这样不断的问下去，最后都会归结于宇宙到底是什么等等这些问题上去。

本篇文章的内容到此结束。

谢谢各位阅读！

以后还会不断更新精心准备的通俗科普长文！