挑战中考数学最后一道压轴题（中考数学压轴题第7期）

中考数学压轴题70

【分析】（1）把点A坐标代入二次函数解析式即求得b的值．

（2）求点B、C、D坐标，求直线BC、BD解析式．设点P横坐标为t，则能用t表示点P、M、N、H的坐标，进而用含t的式子表示PM、MN、NH的长．以PM＝MN为等量关系列得关于t的方程，求得t的值合理（满足P在第一象限），故存在满足条件的点P，且求得点P坐标．

（3）过点P作PF⊥x轴于F，交直线BD于E，根据同角的余角相等易证∠EPQ＝∠OBD，所以cos∠EPQ＝cos∠OBD，即在Rt△PQE中，cos∠EPQ；在Rt△PFR中，cos∠RPF，进而得PQPE，PRPF．设点P横坐标为t，可用t表示PE、PF，即得到用t表示PQ、PR．又由S△PQB＝2S△QRB易得PQ＝2QR．要对点P位置进行分类讨论得到PQ与PR的关系，即列得关于t的方程．求得t的值要注意是否符合各种情况下t的取值范围．

中考数学压轴题71

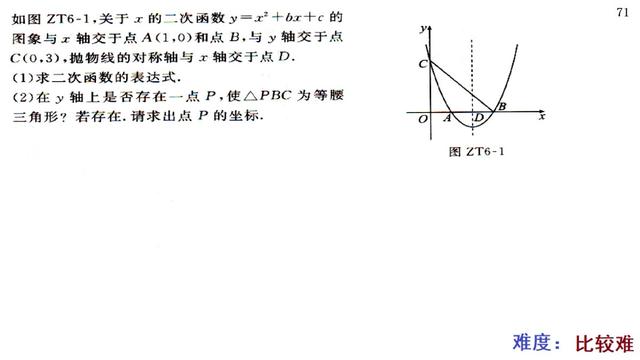
【分析】（1）把A、C坐标代入可求得b、c的值，可求得二次函数表达式；

（2）先求得BC长度，设P点坐标为（2，m），分∠PBC、∠PCB、∠BPC分别为等腰三角形顶角三种情况，分别根据等腰三角形的两腰相等可得到关于m的方程，求得P点坐标；

（3）由条件可知AM＝t，则DN＝2t，分M在线段AD上和在线段BD上，可分别用t表示出△MNC和△MNB的面积，再由条件可得到关于t的方程，可求得t的值．

中考数学压轴题72

【分析】（1）抛物线的表达式为：y＝a（x﹣3）（x 1）＝a（x2﹣2x﹣3），即可求解；

（2）分PA是斜边、PM时斜边、AM是斜边三种情况，分别求解即可；

（3）在△CEH中，CH，∠BEF＝∠HEC＝45°，设：NE＝a，则HN＝a，HEa，CN，EG＝HEsinα，GH，由勾股定理得：CE2＝GE2 CG2，（a）2＝（a）2 （a）2，即可求解．

中考数学压轴题73

【分析】（1）直接用顶点坐标公式求即可；

（2）由对称轴可知点C（2，），A（，0），点A关于对称轴对称的点（，0），借助AD的直线解析式求得B（5，3）；①当n时，N（2，），可求DA，DN，CD当PQ∥AB时，△DPQ∽△DAB，DP＝DP；当PQ与AB不平行时，DP，；②当PQ∥AB，DB＝DP时，DB＝3，DN，所以N（2，），则有且只有一个△DPQ与△DAB相似时，n；

中考数学压轴题74

【分析】（1）先确定出点A的坐标，进而用待定系数法求出抛物线解析式；

（2）先确定出点B的坐标，①设点P（m，﹣m2﹣2m 3），得出PG＝﹣m2﹣3m 4，利用三角形的面积公式建立函数关系式即可得出结论；

②先确定出点E的坐标，进而判断出△BPE是直角三角形，即可作出图形，利用两直线的交点坐标的求法即可得出结论．

中考数学压轴题75

【分析】（1）根据A点坐标，可得c的值，根据对称轴公式，可得b的值；

（2）根据菱形的对称轴垂直且互相平分，可得D是抛物线的顶点；

（3）根据菱形的对角线垂直且互相平分，可得P是直线x＝﹣3与抛物线yx2x﹣4的交点，根据自变量与函数值的对应关系，可得答案；根据正方形的对角线相等且互相平分、垂直，可得答案．

中考数学压轴题76

【分析】（1）令y＝0，解方程即可得到点A、B的坐标，然后根据点的对称性求出点C的坐标，再根据中点定义求出点F的坐标；

（2）把点C的坐标代入一次函数求出m的值，从而得到直线CD的解析式，然后设出点K的坐标，并表示出点H、G的坐标，利用两点间的距离表示出CD，整理后根据二次函数的最值问题求解；

（3）根据直线CD的解析式与抛物线的解析式分别设出点M、N的坐标，然后分①AC是平行四边形的边，根据平行四边形的对边平行且相等分点N在点M的左侧与右侧两种情况分别求出点N是横坐标，然后代入抛物线解析式求出纵坐标，即可得到点N的坐标；②AC是对角线时，根据平行四边形的对角线互相平分可得M、N关于点B对称，根据对称性求出点N的横坐标，然后代入抛物线解析式求出点N的纵坐标，即可得解．

中考数学压轴题77

【分析】（1）根据点M、N的坐标，利用待定系数法即可求出图②中线段MN所在直线的函数表达式；

（2）分FE＝FG、FG＝EG及EF＝EG三种情况考虑：①考虑FE＝FG是否成立，连接EC，通过计算可得出ED＝GD，结合CD⊥EG，可得出CE＝CG，根据等腰三角形的性质可得出∠CGE＝∠CEG、∠FEG＞∠CGE，进而可得出FE≠FG；②考虑FG＝EG是否成立，由正方形的性质可得出BC∥EG，进而可得出△FBC∽△FEG，根据相似三角形的性质可得出若FG＝EG则FC＝BC，进而可得出CG、DG的长度，在Rt△CDG中，利用勾股定理即可求出x的值；③考虑EF＝EG是否成立，同理可得出若EF＝EG则FB＝BC，进而可得出BE的长度，在Rt△ABE中，利用勾股定理即可求出x的值．综上即可得出结论．

中考数学压轴题78

【分析】（1）先确定出点A的坐标，进而求出AP，利用对称性即可得出结论；

（2）分三种情况，①利用正方形的面积减去三角形的面积，②利用矩形的面积减去三角形的面积，③利用梯形的面积，即可得出结论；

（3）先确定出点T的运动轨迹，进而找出OT PT最小时的点T的位置，即可得出结论．

中考数学压轴题79

【分析】将△AMD绕点A逆时针旋转60°得到△AM′D′，则MD＝M′D′，△ADD′和△AMM′均为等边三角形，推出AM＝MM′可得MA MD ME＝D′M MM′ ME，共线时最短；由于点E也为动点，可得当D′E⊥BC时最短，此时易求得D′E＝DG GE的值；

为培养孩子的自主学习能力，提高数学能力，本人特地整理了下面的题目，每个题目质量都比较高，值得大家做一做，看一看，每个题目都有相应的视频讲解，相应视频在视频栏目或视频合集、专栏都有，建议大家先把题目打印下来让孩子先独立做一做，再进行视频学习后批改并订正，坚持下去，数学成绩肯定提高。本专辑及视频将同步更新，纯公益！大家可以及时关注学习。喜欢本专辑及视频就点赞、转发、强烈推荐。[作揖][作揖][作揖]，您的肯定就是我的动力。需要电子稿请私信。