中考几何图形经典例题（全景透视抛物线背景下的几何探究型问题）

二次函数的背景下的几何探究型问题，往往涉及到的知识点较多、关系复杂、条件隐蔽、思路难觅，综合性较强，难度较大．但只要牢记"数形结合记心上，潜在条件不能忘，大题小做来转化，化动为静多画图，分类讨论要严密，方程函数作工具"就一定能迎刃而解．其形式往往出现存在性形式，所谓存在性形式是指根据题目所给的条件，探究是否存在符合要求的结论，此类问题的叙述一般是"是否存在……，如果存在，请求出……(或请证明)；如果不存在，请说明理由，"解决此类问题的一般方法是逆推法，即假设结论存在，根据条件推理、计算，如果求得出一个结果，并根据推理或计算过程每一步的可逆性，证得结论存在；如果推得矛盾的结论或求不出结果，则说明结论不存在．

类型1　探究线段数量关系及最值的存在性

例1．(2018·宜宾中考题)在平面直角坐标系xOy中，已知抛物线的顶点坐标为(2,0)，且经过点(4,1)，如图，直线y＝x/4与抛物线交于A，B两点，直线l为y＝－1.

(1)求抛物线的解析式；

(2)在l上是否存在一点P，使PA＋PB取得最小值？若存在，求出点P的坐标；若不存在，请说明理由．

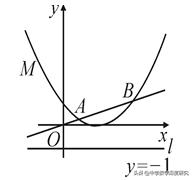
(3)已知F(x0，y0)为平面内一定点，M(m，n)为抛物线上一动点，且点M到直线l的距离与点M到点F的距离总是相等，求定点F的坐标．

【分析】 (1)设顶点式y＝a(x－2) ²，将点(4，1)代入即可求a的值，得出抛物线的解析式；

(2)联立直线AB与抛物线解析式得到点A与点B的坐标，设出点M的坐标为(0，m)，利用等式MA ²＝MB ²，求出点M的坐标；

(3)利用最短线段思想，作点B关于直线l的对称点B′，连接AB′交直线l于点P，此时PA＋PB取得最小值．求出直线AB′解析式后，联立直线l得出点P坐标；

(4)由最短线段思想可知，当S，A，B三点共线时，SB－SA取得最大值．

解：(1)∵抛物线的顶点坐标为(2,0)，∴设抛物线的解析式为y＝a(x－2)2.

∵该抛物线经过点(4,1)，∴1＝4a，解得a＝1/4，∴抛物线的解析式为y＝1/4 (x－2) ²＝1/4x ²－x＋1.

(2)联立直线AB与抛物线解析式成方程组，

∴点A的坐标为(1，1/4)，点B的坐标为(4,1)．

如答图，作点B关于直线l的对称点B′，连接AB′交直线l于点P，此时PA＋PB取得最小值．

∵点B(4,1)，直线l为y＝－1，∴点B′的坐标为(4，－3)．

设直线AB′的解析式为y＝kx＋b(k≠0)，

将A(1，1/4)，B′(4，－3)分别代入y＝kx＋b，得k b=1/4,4k b=-3,

解得k=-13/12, b=4/3.

∴直线AB′的解析式为y＝－13/12x＋4/3.当y＝－1时，有－13/12x＋4/3＝－1，

解得x＝28/13，∴点P的坐标为(28/13，－1)．

【方法规律】直线同侧两点到直线上一点距离和最小问题，要通过轴对称将直线同侧两点转化为直线异侧两点，连接对称点与另一点交直线上一点，此点即为直线上的点到同侧两点距离和最小的点。

例2.（2018•广西中考题）如图，抛物线y＝ax²﹣5ax c与坐标轴分别交于点A，C，E三点，其中A（﹣3，0），C（0，4），点B在x轴上，AC＝BC，过点B作BD⊥x轴交抛物线于点D，点M，N分别是线段CO，BC上的动点，且CM＝BN，连接MN，AM，AN．

（1）求抛物线的解析式及点D的坐标；

（2）当△CMN是直角三角形时，求点M的坐标；

（3）试求出AM AN的最小值．

【分析】（1）利用待定系数法求抛物线解析式；利用等腰三角形的性质得B（3，0），然后计算自变量为3所对应的二次函数值可得到D点坐标；

（3）连接DN，AD，如图，先证明△ACM≌△DBN，则AM＝DN，所以AM AN＝DN AN，利用三角形三边的关系得到DN AN≥AD（当且仅当点A、N、D共线时取等号），然后计算出AD即可．

【解答】（1）把A（﹣3，0），C（0，4）代入y＝ax²﹣5ax c得9a 15a c=0,c=4，解得a=-1/6,c=4，

∴抛物线解析式为y＝﹣1/6x² 5/6x 4；

∵AC＝BC，CO⊥AB，∴OB＝OA＝3，∴B（3，0），

∵BD⊥x轴交抛物线于点D，∴D点的横坐标为3，

当x＝3时，y＝﹣1/6×9 5/6×3 4＝5，∴D点坐标为（3，5）；

（3）连接DN，AD，如图，∵AC＝BC，CO⊥AB，∴OC平分∠ACB，∴∠ACO＝∠BCO，

∵BD∥OC，∴∠BCO＝∠DBC，

∵DB＝BC＝AC＝5，CM＝BN，∴△ACM≌△DBN，

∴AM＝DN，∴AM AN＝DN AN，

而DN AN≥AD（当且仅当点A、N、D共线时取等号），

【方法点评】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质和相似三角形的判定与性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会运用分类讨论的思想解决数学问题．

在解决二次函数与几何问题的综合问题时，相似是常见手段，在遇到陌生问题的时候，要善于运用已学知识进行转化，转化为熟悉的问题来解决．

例3．(2018·烟台中考题)如图1，抛物线y＝ax ²＋2x＋c与x轴交于A(－4,0)，B(1,0)两点，过点B的直线y＝kx＋2/3分别与y轴及抛物线交于点C，D.

(1)求直线和抛物线的表达式；

(2)动点P从点O出发，在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动，设运动时间为t秒，当t为何值时，△PDC为直角三角形？请直接写出所有满足条件的t的值；

(3)如图2，将直线BD沿y轴向下平移4个单位后，与x轴，y轴分别交于E，F两点，在抛物线的对称轴上是否存在点M，在直线EF上是否存在点N，使DM＋MN的值最小？若存在，求出其最小值及点M，N的坐标；若不存在，请说明理由．

【分析】（1）∵抛物线y＝ax ²＋2x＋c和x轴交点A（－4，0），B（1，0），∴设y=a(x 4)(x-1)， 展开后让一次项系数等于2，可求出a，从而求出抛物线的表达式；

（2）此题分类讨论，先以BD为直径画圆和x轴交于两点；再分别过D和C两点作CD的垂线，分别与x轴交于两点，都是符合条件的点，共有四个点．每一种情况都可以通过三角函数（或相似）解决；

(3)此题D是定点，M、N是动点，这与我们以前遇到的求一动点到两定点的距离之和最小不同，但也有共同之处，就是都需要过定点作对称轴的对称点．此题也不例外，就是作D关于对称轴的对称点D'，再根据垂线段最短，过D'作直线EF的垂线，垂足为N，垂线D'N与直线EF交于点M，此时M、N即为所求点，再利用D′N⊥EF，得到：

从而求出直线D′N的表达式，与直线EF的表达式联立求出N的坐标；又M的横坐标可通过对称轴x=-3/2确定，将M的的横坐标x=-3/2代入直线D′N的表达式，可求出M的坐标．DM＋MN的最小值即为D′N的长度，可以通过D'和N的坐标，利用两点间距离公式得到．

【解答】（1）方法1：∵A（－4，0），B（1，0），

∴设y=a(x 4)(x-1)，∴y=ax ² 3ax-4a，

∴3a＝2，∴a=2/3，∴y=2x ²/3 2x-8/3．

把B（1，0）代入y=kx 2/3，可得k=-2/3，∴y=-2/3x 2/3．

方法2：把A（－4，0），B（1，0）代入y=ax ² 2x c，得

0=16a-8 c, 0=a 2 c,

解得a=2/3,c=-8/3,∴y=2x ²/3 2x-8/3．

把B（1，0）代入y=kx 2/3，，可得k=-2/3，∴y=-2/3x 2/3．

Ⅰ)若∠DPC＝90°，如图（1），作DH⊥x轴于H，∴∠1＋∠2＝90°＝∠3＋∠2，∴∠1＝∠3，

∴tan∠1＝tan∠3，∵P（－t，0），∴PH＝5－t，OP＝t，

【方法规律】（1）二次函数图象与其他函数图象相结合问题：解决此类问题时，先根据给定的函数或函数图象判断出系数的符号，然后判断新的函数关系式中系数的符号，再根据系数与图象的位置关系判断出图象特征，则符合所有特征的图象即为正确选项．

（2）二次函数与方程、几何知识的综合应用：将函数知识与方程、几何知识有机地结合在一起．这类试题一般难度较大．解这类问题关键是善于将函数问题转化为方程问题，善于利用几何图形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件．

类型2　探究角度数量关系的存在性

例4．抛物线y＝﹣x ² 2x 3与x轴交于点A，B（A在B的左侧），与y轴交于点C．

（1）求直线BC的解析式；

（2）抛物线的对称轴上存在点P，使∠APB＝∠ABC，利用图1求点P的坐标；

（3）点Q在y轴右侧的抛物线上，利用图2比较∠OCQ与∠OCA的大小，并说明理由．

【分析】（1）由抛物线解析式可求得B、C的坐标，利用待定系数法可求得直线BC的解析式；

（2）由直线BC解析式可知∠APB＝∠ABC＝45°，设抛物线对称轴交直线BC于点D，交x轴于点E，结合二次函数的对称性可求得PD＝BD，在Rt△BDE中可求得BD，则可求得PE的长，可求得P点坐标；

（3）设Q（x，﹣x ² 2x 3），当∠OCQ＝∠OCA时，利用两角的正切值相等可得到关于x的方程，可求得Q点的横坐标，再结合图形可比较两角的大小．

【解答】（1）在y＝﹣x ² 2x 3中，令y＝0可得0＝﹣x ² 2x 3，解得x＝﹣1或x＝3，令x＝0可得y＝3，∴B（3，0），C（0，3），

∴可设直线BC的解析式为y＝kx 3，

把B点坐标代入可得3k 3＝0，解得k＝﹣1，∴直线BC解析式为y＝﹣x 3；

（2）∵OB＝OC，∴∠ABC＝45°，

∵y＝﹣x ² 2x 3＝﹣（x﹣1）2 4，

∴抛物线对称轴为x＝1，

设抛物线对称轴交直线BC于点D，交x轴于点E，当点P在x轴上方时，如图1，

∵∠APB＝∠ABC＝45°，且PA＝PB，

∴∠PBA＝（180°-45°）/2＝67.5°，∠DPB＝1/2∠APB＝22.5°，

∴∠PBD＝67.5°﹣45°＝22.5°，∴∠DPB＝∠DBP，∴DP＝DB，

在Rt△BDE中，BE＝DE＝2，由勾股定理可求得BD＝2√2，

∴PE＝2 2√2，∴P（1，2 2√2）；

当点P在x轴下方时，由对称性可知P点坐标为（1，﹣2﹣2√2）；

综上可知P点坐标为（1，2 2√2）或（1，﹣2﹣2√2）；

（3）设Q（x，﹣x² 2x 3），当点Q在x轴下方时，如图2，过Q作QF⊥y轴于点F，

当∠OCA＝∠OCQ时，则△QFC∽△AOC，

∴当Q点横坐标为5时，∠OCA＝∠OCQ；

当Q点横坐标大于5时，则∠OCQ逐渐变小，故∠OCA＞∠OCQ；

当Q点横坐标小于5且大于0时，则∠OCQ逐渐变大，故∠OCA＜∠OCQ．

【方法点评】本题为二次函数的综合应用，涉及待定系数法、等腰三角形的判定和性质、勾股定理、相似三角形的判定和性质、方程思想和分类讨论思想等知识．在（1）中求得B、C坐标是解题的关键，在（2）中构造等腰三角形求得P到x轴的距离是解题的关键，在（3）中确定出两角相等时Q点的位置是解题的关键．本题考查知识点较多，综合性较强，难度适中．

例5．如果三角形的两个内角α与β满足2α β＝90°，那么我们称这样的三角形为"准互余三角形"．

（1）若△ABC是"准互余三角形"，∠C＞90°，∠A＝50°，则∠B═______ °；

（2）如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝5，若AD是∠BAC的平分线，

①判断：△ABD______ （填"是"或"不是"）"准互余三角形"．

②试问在边BC上是否存在点E（异于点D），使得△ABE也是"准互余三角形"？若存在，请求出BE的长，若不存在，请说明理由．

【分析】（1）由题意得：∠A 2∠B＝90°，∠A＝50°即可求解；

（2）①是．设∠A＝2α，∠B＝β，而∠A ∠B＝90°，即：2α β＝90°；②存在，如图①，连结AE，利用△CAE∽△CBA，即可求解；

（3）由题意得：D是线段BC的中点，则：S△BOC＝2S△OCD＝1/2•BO•c，求出BO＝

√3c，而OC＝c，tan∠CBO＝OC/OB=√3/3，∴∠CBO＝30°，即可求解．

【解答】（1）由题意得：∠A 2∠B＝90°，∠A＝50°，则：∠B＝20°，

故：答案为20°；

（2）①是．设∠A＝2α，∠B＝β，而∠A ∠B＝90°，即：2α β＝90°；

故：答案是：是；

②存在，如图，连结AE，

∵△ABE也是"准互余三角形"，∴∠B 2∠BAE＝90°，

∵∠B ∠BAE ∠EAC＝90°，∴∠EAC＝∠B，又∵∠C＝∠C，∴△CAE∽△CBA，∴CA/CB=CE/CA，

即CA2＝CB•CE，∵AC＝4，BC＝5，∴CE＝16/5．

∴BE=BC-CE=5-16/5=9/5；

若∠CBO＝30°＝α，由2α β＝90°得：β＝30°，即：∠CAB＝30°，

若∠CAB＝30°＝α，由2α β＝90°得：β＝30°，即：∠CBO＝30°，

即∠CAB＝∠CBA＝30°，

则：OA＝OB＝2√3，OC＝2，

即：点A、B、C的坐标分别为（﹣2√3，0）、（2√3，0）、（0，2），

【方法点评】本题考查的是二次函数知识的综合运用，涉及到三角形相似、一元二次方程解法等相关知识，本题（2）是难点，其核心是确定△CAE∽△CBA．

（配套练习课私信与我，回及时发送）

综上所述，解答二次函数几何探究性问题时，要注意以下三点：①题目中多个知识点时，这时不妨把不同的知识点层层剥离开来，转化为一个小问题来分析，这样思路就清晰的多；②存在探索性问题，应先假设结论成立，然后运用有关数学知识求解. 善于将函数问题转化为方程问题，善于利用几何图形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件；对于数形结合的思想的应用要注意几何图形的性质为相应的函数或方程提供的条件的应用．这类问题应充分利用"数形结合"的思想，按照"解析式→坐标→距离（线段长度）→几何图形性质及应用"的思路思考；（3）在运动中求最大值或最小值时，通常可以考虑将问题转化为函数的最值讨论问题，利用二次函数的顶点坐标或函数取值范围解决；对于数形结合的思想的应用要注意几何图形的性质为相应的函数或方程提供的条件的应用．

,