高等数学矩阵怎么计算（高等数学矩阵的定义）

矩阵的定义

由m个方程n个未知量x1，x2，…，xn构成的线性（即：一次）方程组可以表示为

在线性方程组中，未知量用什么字母表示无关紧要，重要的是方程组中未知量的个数以及未知量的系数和常数项．也就是说，线性方程组（1-1）由常数

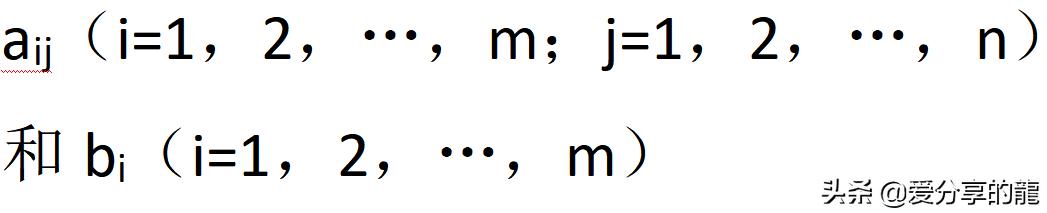
完全确定，所以可以用一个m×（n 1）个数排成的m行n 1列的数表

来表示线性方程组（1-1）．

这个数表的第j（j=1，2，…，n）列表示未知量xj（j=1，2，…，n）前的系数，第i（i=1，2，…，m）行表示线性方程组（1-1）中的第i（i=1，2，…，m）个方程

任意给定一个m行n 1列的数表，可以通过这个数表写出一个线性方程组．因此，线性方程组与这样的数表之间有了一个对应关系

定义1

m×n个数

排成的m行n列的数表

一般地，常用英文大写字母A，B，…或字母α，β，γ，…表示矩阵，如

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵

矩阵除特别指明外，都是指实矩阵

1×1的矩阵A=（a）就记为A=a

1×n的矩阵

称为行矩阵，也称为n维行向量

n×1的矩阵

称为列矩阵，也称为n维列向量

所有元素都是零的m×n矩阵称为零矩阵，记为

n×n矩阵

称为n阶方阵

所在的位置称为n阶方阵的主对角线

一个n阶方阵主对角线上方的元素全为零，即

称该n阶方阵为下三角矩阵

下三角矩阵的元素特点是：当i<j时

类似地，有上三角矩阵

上三角矩阵的元素特点是：当i>j时 aij=0

n阶方阵

称为n阶对角矩阵，简称对角阵，记为

定义2

两个矩阵的行数相等、列数也相等，则称这两个矩阵为同型矩阵

如果两个同型矩阵

则称矩阵A和B相等，记为A=B

,