高中数学导数常见公式（高中数学常用公式及结论）

一 、f（x）在 x0 处的导数（或变化率）：

图（1）

① 瞬时速度：

瞬时速度图

② 瞬时加速度

瞬时加速度图

二、 函数 y = f（x）在点 x0 处的导数的几何意义：

函数 y = f（x）在点 x0 处的导数是曲线 y = f（x）在点 P（x0 , f（x0）) 处的切线的斜率 f '（x0）;

相应的切线方程是： y - y0 = f '（x0）（x - x0）。

三、几种常见函数的导数：

① C' = 0 （C 为常数）；

② 幂函数

幂函数求导公式图

③ 三角函数

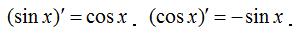
正弦和余弦函数求导公式图

④ 指数函数

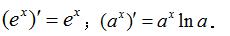
指数函数求导公式图

⑤ 对数函数

对数函数求导公式图

四、导数的运算法则：

导数的运算法则图

五、复合函数的导数：

复合函数求导公式图

六、导数在函数中的应用：

① 函数 y = f（x）在区间 （a , b）的单调性与导数

单调性图

② 判别 f （x0）是极大（小）值的方法：

当函数 f（x）在点 x0 处连续时，

（1）如果在 x0 附近的左侧 f '（x0）> 0 ，右侧 f '（x0）< 0，则 f （x0）是极大值；

（2）如果在 x0 附近的左侧 f '（x0）< 0，右侧 f '（x0）> 0，则 f （x0） 是极小值 。

七、定积分的性质：

①

定积分的性质图（1）

②

定积分的性质图（2）

③

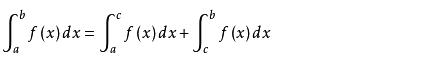
定积分的性质图（3）

④ 如果在闭区间 [a,b] 上，f(x) ≥0 , 则

定积分的性质图（4）

八、微积分基本定理：

如果函数 f(x) 是闭区间 [a,b] 上的连续函数，并且有 F′(x) = f(x)，那么有

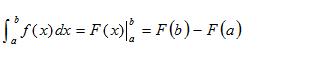
微积分基本定理图

九、定积分的几何意义：

由连续曲线 y = f（x）（ f（x）≥ 0 ）和 x = a , x = b 及 y = 0 围成的平面图形 AabB 称为曲边梯形，如下图所示：

定积分的几何意义图（1）

① 若 f（x）≤ 0 （如下图所示）则曲边梯形的面积为

定积分的几何意义图（2）

② 把由直线 y = c，y = d (c < d )及两条连续曲线 x = g1(y)，x = g2(y) ( g1(y) ≤ g2(y)) 所围成的平面图形称为Y－型图形。

定积分几何意义图（3）

图中阴影部分的面积：

求图中阴影部分面积公式图（1）

③ 由连续曲线 y = f1（x）, y = f2（x）和 直线 x = a , x = b 围成的图形的面积 。

定积分几何意义图（3）

图中阴影部分的面积：

求图中阴影部分面积公式图（2）

十、定积分在物理上的应用

① 变速 v = v（t）（t ≥ 0） 时间在 [ a , b ] 段 ，路程

定积分在物理上的应用图（1）

② 变力 F = F（x）, 物体沿力的方向从 a 移动到 b ，做功

定积分在物理上的应用图（2）

,