李老师讲数学经典面积题（动点产生的面积关系问题）

1．求不规则图形或难以同时求出底和高的三角形的面积，一般的思路是割补法：

①有一边“水平”或“竖直”的多边形，作垂线分割成直角三角形或直角梯形，如图1；

②“斜”的三角形一般不易找到它的底和高，通常过顶点作铅垂线和水平线“补”成矩形，再减去各角上的直角三角形面积，如图2．

图1

图2

2．对于“斜”三角形可用“铅垂法”求面积：如图3，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”（h）．我们可得出一种计算三角形面积的新方法：S_△ABC＝1/2ah，即三角形面积等于水平宽与铅垂高乘积的一半．

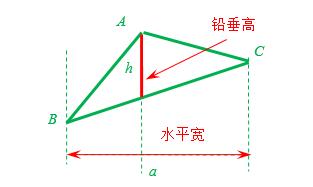
图3

3．底或高不明显，但已知边的关系，可用相似比间接求得．①如图4，同底三角形的面积比等于高的比同高三角形的面积比等于底的比；②如图5，同底等高三角形的面积相等．

图4

图5

【典型例题】

如图①，已知抛物线y＝ax²＋bx＋3（a≠0）与x轴交于点A（1，0）和点B（－3，0），与y轴交于点C．

（1）求抛物线的解析式；

（2）设抛物线的对称轴与x轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

（3）如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．