粒子算法优化背包问题matlab（粒子群优化算法解决TSP问题及Matlab代码）

1、粒子群算法简介

粒子群优化算法(Particle Swarm Optimization——PSO）， 由James Kennedy（社会心理学博士）和Russell Eberhart（电子工程学博士，于1995年提出的一种基于种群的随机优化算法。

鸟被抽象为没有质量和体积的微粒(点)，并延伸到N维空间，粒子I 在N维空间的位置表示为矢量Xi＝(x1，x2，…，xn)，飞行速度表示为矢量Vi＝(v1，v2，…，vn),每个粒子都有一个由目标函数决定的适应值(fitness value)；并且知道自己到目前为止发现的最好位置(pbest)；除此之外，每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest)(gbest是pbest中的最好值)。　　　

2、粒子群算法核心概念

如果鸟群觅食的过程中会有信息的交流，则每一个小鸟都会向最优的路径进行觅食的。每一个小鸟其对应的位置矢量和速度矢量，所以在寻优的过程中会对每一个粒子的位置和速度进行更新。

其中（1）式为粒子i在第k 1次迭代时的速度更新公式，（2）式为相对应的位置更新公式。

rand()是介于0~1之间的实数，ω为惯性因子，c1为个体学习因子，c2为群体认知因子。

从社会学的角度来看，公式(1)的第一部分称为记忆项，表示上次速度大小和方向的影响；公式第二部分称为自身认知项，是从当前点指向粒子自身最好点的一个矢量，表示粒子的动作来源于自己经验的分；公式的第三部分称为群体认知项，是一个从当前点指向种群最好点的矢量，反映了粒子间的协同合作和知识共享。

粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。ω值较大，全局寻优能力强，局部寻优能力弱，ω较小，则反之。初始时，ω取为常数，后来实验发现，动态能够获得比固定值更好的寻优结果。动态可以在PSO搜索过程中线性变化，也可根据PSO性能的某个测度函数动态改变。

在解决TSP问题中，每一个粒子相当于遗传算法中的每一个个体，粒子的位置则相当于该个体访问所有城市的路径，粒子的速度则是一个交换序列的矩阵。该交换序列是把个体最优或群体最优的粒子与粒子群的路径关系。就是说在最优个体的粒子其中一个元素在待优化的粒子中的位置记录下来，并且在接下来的更新粒子位置时，尽量复制最优个体的元素序列。

3、粒子群算法流程

Step1:初始化一群微粒(群体规模为M)，包括随机位置和速度；

Step2:评价每个微粒的适应度；

Step3:对每个微粒，将其适应值与其经过的最好位置pbest作比较，如果较好，则将其作为当前的最好位置pbest;

Step4:对每个微粒，将其适应值与其经过的最好位置gbest作比较，如果较好，则将其作为当前的最好位置gbest;

Step5:根据(1)、(2)式调整微粒速度和位置；

Step6:未达到结束条件则转Step2。

4、粒子群算法实例及代码

解决TSP问题的Matlab代码如下:

function Psorout = PSO_TSP(xy,dmat,Popsize,IterNum,showProg,showResult) %利用粒子群优化算法解决TSP问题 nargs = 6;%代表函数要输入参数的个数 for i = nargin:nargs-1 switch i case 0 %产生城市数据 xy = [488,814;1393,595;2735,2492;4788,4799;4825,1702;789,2927;4853,1120;4786,3757;2427,1276;4002,2530;710,3496;2109,4455;4579,4797;3962,2737;4798,694;3279,747;179,1288;4246,4204;4670,1272;3394,4072;3789,1218;3716,4647; 1962,1750]; % xy = 5000*rand(39,2);%产生40个城市坐标40*2矩阵 case 1 %计算距离矩阵 N = size(xy,1); a = meshgrid(1:N);%生成N*N升序矩阵 dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),N,N);% '为矩阵的转置，reshape把数据生成N*N的矩阵 case 2 %设置粒子群数目 Popsize = 500; case 3 %设置迭代次数 IterNum = 2000; case 4 %是否展示迭代过程 showProg = 1; case 5 %是否展示结果 showResult = 1; otherwise end end %对输入参数进行检查 [N,~] = size(xy);%城市个数、维数 [nr,nc] = size(dmat);%距离矩阵的行数和列数 if N~=nr || N~=nc error('城市坐标或距离矩阵输入有误') end showProg = logical(showProg(1));%将数值转变为逻辑值 showResult = logical(showResult(1)); %画出城市位置分布图 figure(1); plot (xy(:,1),xy(:,2),'k.','MarkerSize',14); title('城市坐标位置'); %% PSO参数初始化 c1 = 0.1; %个体学习因子 c2 = 0.075; %社会学习因子 w = 1; %惯性因子 pop = zeros(Popsize,N); %粒子位置 v = zeros(Popsize,N); %粒子速度 iter = 1; %迭代次数计时 fitness = zeros(Popsize,1); %适应度函数值 Pbest = zeros(Popsize,N); %个体极值路径 Pbest_fitness = zeros(Popsize,1); %个体极值 Gbest = zeros(IterNum,N); %群体极值路径 Gbest_fitness = zeros(Popsize,1); %群体极值 Length_ave = zeros(IterNum,1); ws = 1; %惯性因子最大值 we = 0.5; %惯性因子最小值 %% 产生初始位置和速度 for i = 1:Popsize pop(i,:) = randperm(N); v(i,:) = randperm(N); end %计算粒子适应度值 for i =1:Popsize for j =1:N-1 fitness(i) = fitness(i) dmat(pop(i,j),pop(i,j 1)); end fitness(i) = fitness(i) dmat(pop(i,end),pop(i,1));%加上终点回到起点的距离 end %计算个体极值和群体极值 Pbest_fitness = fitness; Pbest = pop; [Gbest_fitness(1),min_index] = min(fitness); Gbest(1,:) = pop(min_index); Length_ave(1) = mean(fitness); %% 迭代寻优 while iter <IterNum %更新迭代次数与惯性系数 iter = iter 1; w = ws-(ws-we)*(iter/IterNum)^2;%动态惯性系数 %更新速度 %个体极值序列交换部分 change1 = positionChange(Pbest,pop); change1 = changeVelocity(c1,change1);%是否进行交换 %群体极值序列交换部分 change2 = positionChange(repmat(Gbest(iter-1,:),Popsize,1),pop);%将Gbest复制成m行 change2 = changeVelocity(c2,change2); %原速度部分 v = OVelocity(w,v); %修正速度 for i = 1:Popsize for j =1:N if change1(i,j) ~= 0 v(i,j) = change1(i,j); end if change2(i,j) ~= 0 v(i,j) = change2(i,j); end end end %更新粒子位置 pop = updatePosition(pop,v);%更新粒子的位置，也就是更新路径序列 %适应度值更新 fitness = zeros(Popsize,1); for i = 1:Popsize for j = 1:N-1 fitness(i) = fitness(i) dmat(pop(i,j),pop(i,j 1)); end fitness(i) = fitness(i) dmat(pop(i,end),pop(i,1)); end %个体极值与群体极值的更新 for i =1:Popsize if fitness(i) < Pbest_fitness(i) Pbest_fitness(i) = fitness(i); Pbest(i,:) = pop(i,:); end end [minvalue,min_index] = min(fitness); if minvalue <Gbest_fitness(iter-1) Gbest_fitness(iter) = minvalue; Gbest(iter,:) = pop(min_index,:); 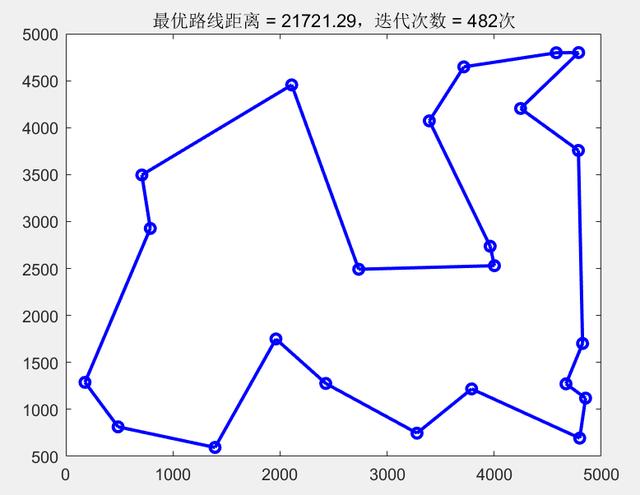if showProg figure(2); for i = 1:N-1 %画出中间段 plot([xy(Gbest(iter,i),1),xy(Gbest(iter,i 1),1)],[xy(Gbest(iter,i),2),xy(Gbest(iter,i 1),2)],'bo-','LineWidth',2); hold on; end plot([xy(Gbest(iter,end),1),xy(Gbest(iter,1),1)],[xy(Gbest(iter,end),2),xy(Gbest(iter,1),2)],'bo-','LineWidth',2); title(sprintf('最优路线距离 = %1.2f，迭代次数 = %d次',minvalue,iter)); hold off end else Gbest_fitness(iter) = Gbest_fitness(iter-1); Gbest(iter,:) = Gbest(iter-1,:); end Length_ave(iter) = mean(fitness); end %% 结果显示 [Shortest_Length,index] = min(Gbest_fitness); BestRoute = Gbest(index,:); if showResult figure(3); plot([xy(BestRoute,1);xy(BestRoute(1),1)],[xy(BestRoute,2);xy(BestRoute(1),2)],'o-') grid on xlabel('城市位置横坐标'); ylabel('城市位置纵坐标'); title(sprintf('粒子群算法优化路径最短距离：%1.2f',Shortest_Length)); figure(4); plot(1:IterNum,Gbest_fitness,'b',1:IterNum,Length_ave,'r:') legend('最短距离','平均距离'); xlabel('迭代次数'); ylabel('距离') title('各代最短距离与平均距离对比'); end if nargout Psorout{1} = BestRoute; Psorout{2} = Shortest_Length; end end function change = positionChange(best,pop) %记录将pop变成best的交换序列 for i = 1:size(best,1) for j =1:size(best,2) change(i,j) = find(pop(i,:)==best(i,j));%在粒子i中找到best(i,j)位置索引 temp = pop(i,j);%将序列交换 pop(i,j) = pop(i,change(i,j)); pop(i,change(i,j)) = temp; end end end function change = changeVelocity(c,change) %以一定的概率保留序列 for i =1:size(change,1) for j = 1:size(change,2) if rand > c change(i,j) = 0; end end end end function v = OVelocity(c,v) %以一定的概率保留上一次迭代的交换序列 for i =1:size(v,1) for j = 1:size(v,2) if rand >c v(i,j) = 0; end end end end function pop = updatePosition(pop,v) %利用速度记录的交换序列进行位置的更新 for i = 1:size(pop,1) for j =1:size(pop,2) if v(i,j) ~= 0 temp = pop(i,j); pop(i,j) = pop(i,v(i,j)); pop(i,v(i,j)) = temp; end end end end

结果如下：

若有小伙伴对机器人任务分配算法较为兴趣的，可以在下面评论交流一波，纯属互相学习!