山体垂直带谱的复杂程度影响因素（结合注意力机制和Bi-LSTM的降雨型滑坡位移预测）

本文内容来源于《测绘通报》2022年第9期，审图号：GS京（2022）0710号

结合注意力机制和Bi-LSTM的降雨型滑坡位移预测

唐菲菲¹, 唐天俊^1,2, 朱洪洲³, 胡川¹, 马英¹, 李昕⁴

1. 重庆交通大学智慧城市学院, 重庆 400074;

2. 重庆工商职业学院城市建设工程学院, 重庆 400052;

3. 重庆交通大学交通土建工程材料国家地方联合工程实验室, 重庆 400074;

4. 长安大学地质工程与 测绘学院, 陕西 西安 710054

基金项目：国家重点研发计划(2021YFB2600603);重庆市教委科学技术研究项目(KJQN201900728)

关键词：降雨型滑坡, 位移预测, 时间序列分解, 注意力机制, 双向长短时记忆神经网络

引文格式：唐菲菲, 唐天俊, 朱洪洲, 等. 结合注意力机制和Bi-LSTM的降雨型滑坡位移预测[J]. 测绘通报, 2022(9): 74-79,104. DOI: 10.13474/j.cnki.11-2246.2022.0267.

摘要

摘要：受季节降雨波动和邻近点位的牵引作用影响,滑坡位移呈阶梯状变化趋势。为有效预测该类滑坡的位移,本文提出一种基于注意力机制的双向长短时记忆(Bi-LSTM)神经网络位移预测模型。首先,建立滑坡监测累计位移时间序列模型,将滑坡累计位移分解为趋势项和周期项;然后,分析滑坡因子与趋势项及周期项的相关性,采用多项式回归对趋势项进行拟合,通过基于注意力机制的Bi-LSTM对周期项进行预测。试验结果表明:基于注意力机制的Bi-LSTM预测模型具有稳健的泛化能力,能有效捕获不同时序数据间的相关性;预测结果精度平均绝对误差为0.088 mm,平均均方误差为0.042 mm,相比常规的长短时记忆(LSTM)神经网络模型,本文方法的预测结果精度更高。

正文

滑坡的早期预报能有效减少灾害损失。近年来，针对降雨型滑坡的早期预报研究主要有4类：①通过统计分析及经验公式建立滑坡降雨临界阈值或降雨阈值^[1-2]；②通过降雨参数及降雨发生的次数，采用统计分析的方法建立降雨滑坡概率模型，根据降雨参数预测滑坡发生滑坡概率^[3-4]；③通过对力学、土力学、渗流等作用影响的分析，对滑坡的边坡稳定性进行判定^[5-6]；④通过物理模型和数学模型预测滑坡位移进行早期预警^[7-8]。

随着模式识别及机器学习理论的发展，非线性理论被广泛运用于滑坡位移预测，滑坡位移的预测理论和方法得到了快速发展。文献[9]将粗糙集和支持向量机进行有机结合预测白水河位移，通过粗糙集对冗余数据剔除后，预测模型具有较强的泛化能力。同时，由于滑坡位移数据属于时间序列，滑坡历史数据与未来数据具有相关性，滑坡因子同时影响变形及下一时序的稳定性条件^[10]，因此，将时间序列的分析方法引入滑坡位移预测，能有效利用不同时间滑坡位移数据的时序相关性。基于这一思想，文献[11]采用循环神经网络(recurrent neural network，RNN)对白水河滑坡位移进行预测，其预测性能较BP(back propagation)神经网络更加稳健。此外，虽然RNN能记忆历史信息，并预测出当前时序输出，但RNN对于长序列容易出现梯度消失。为解决RNN的序列长期依赖问题，长短时记忆(long-short term memory，LSTM)^[12]随之出现。文献[13]采用LSTM预测白家堡位移，泛化能力比后向传播网络及支持向量回归机更强。LSTM能通过门控系统记忆和遗忘数据，但LSTM隐藏层共享参数会导致细节信息丢失。为解决这一问题，本文将注意力机制引入滑坡预测。注意力机制^[14]在深度学习领域，特别是在图像处理、语音识别和自然语言处理的任务中广泛使用，但在滑坡预测运用尚少。本文将注意力机制与LSTM相结合，一定程度上克服了LSTM预测方法的局限性，提升了模型的泛化能力。

本文首先通过时间序列分解，将累计位移分解为趋势项位移和周期项位移。然后，通过多元回归法对预测点位的趋势项位移进行预测，同时以基于注意力机制的双向长短时记忆(bidirectional LSTM，Bi-LSTM)神经网络作为编码器，常规LSTM神经网络作为解码器实现周期项位移的预测。

1 基于注意力机制的Bi-LSTM降雨型滑坡位移预测方法

本文提出的滑坡位移预测模型架构包括数据预处理层、数据预测层、模型验证层(如图 1所示)。其中，数据预处理层对滑坡累计位移数据进行时间序列分解，构造数据集；数据预测层分为趋势项预测和周期项预测，趋势项和周期项分别采用多元回归法和基于注意力机制的Bi-LSTM模型进行预测，将趋势项和周期项预测值相加获得累计位移预测值；模型验证层以测试集的累计位移预测值与测量值的误差值验证模型预测稳健性，并根据验证结果调整模型。

图 1滑坡位移预测模型框架

1.1 数据预处理层

数据预处理层通过时间序列分解，将累计位移分解为趋势项、周期项和随机项。长期来看，趋势项主要受内部地质条件、地质结构等影响^[15]，该类影响属于长期影响，因此趋势项呈现单调递增的趋势。然而，周期项主要受外部滑坡因素影响(如降雨、水位库水位等)，影响因素作用时间短，且具有一定的周期性，因此，周期项波动近似周期函数。随机项则受偶然荷载影响，相对趋势项和周期项较小，本文忽略不计。经过上述分析，本文建立时间序列分解模型，将累计位移分解为

(1)

式中，X(t)为累计位移；S(t)为趋势项；V(t)为周期项。

受降雨及地质内部条件的影响，降雨型滑坡位移曲线呈阶梯状增长。为分离周期项和趋势项，文献[16]提出移动平均法消除短期的周期项，从而获取趋势项。本文采用文献[16]方法提取滑坡累计位移趋势项。移动平均法公式为

(

2)

式中，φt为对下一期的预测值；n为移动平均周期长度；st-n为前一期至前n期的观测值。通过移动平均法，对累计位移曲线进行平滑，去除由外部滑坡因素影响导致的滑坡位移扰动，即认为得到位移趋势项。将原累计位移与趋势项相减，得到周期项，即实现了周期项与趋势项的分离。

1.2 数据预测层

数据预测层分别对趋势项和周期项进行预测。趋势项通过多项式回归预测，周期项则采用基于注意力机制的Bi-LSTM预测。预测层网络结构(如图 2所示)分为编码器(Bi-LSTM)、注意力机制、解码器(LSTM)。

图 2基于注意力机制的Bi-LSTM

在该网络结构中，Bi-LSTM作为编码器，利用前向LSTM和后向LSTM两个方向上的时序数据提取特征序列，可以有效提取训练集的前后时序特征。同时，本文在Bi-LSTM层后引入注意力机制，根据(t-1)时刻预测值对t时刻的隐藏层输出向量分配合适的注意力权重，以生成与该时序预测值相关的特征序列。经过注意力机制层分配后的特征向量被进一步输入LSTM层进行解码，通过一层全连接层后得到预测值。LSTM作为解码器可以充分发挥其时间序列处理的优势，有效记录时间序列长期依赖信息。

1.3 模型训练

为提高模型预测的稳健性，本文模型训练将采用Huber Loss^[17]进行梯度下降参数寻优，相比于最小二乘的线性回归，Huber Loss降低了离群点的惩戒程度，提高了模型的泛化能力。当预测误差小于δ时，采用平方误差；当预测偏差大于δ时，采用的线性误差。Huber Loss定义为

(

3)

式中，Lδ为损失函数；a为误差项，即真实值与预测值之差；δ为Huber loss参数，设定为1.25。

2 试验与结果分析2.1 滑坡概况

滑坡区地处长江右岸，上游至库尾(重庆市)425 km，下游至库首(三峡大坝)182 km，北抵长江，东至奉节县城20 km。滑坡后缘高程为390~400 m，前缘长江枯水期水面标高为175 m，相对高差为215~225 m。由于滑坡的活动，在坡面上形成三级台地，各台地的总体走向与山体坡面走向一致，台面宽100~250 m，长为700~1400 m，台面坡度5°~12°。滑坡区域内有3条较大的冲沟发育，沟深为5~15 m，沟谷走向与斜坡倾向一致，沟床纵坡降为25%左右，与坡面近于一致。冲沟均无常年性流水，一般在降水过后保持3~5 d水流，为雨源型冲沟。

该滑坡区域多年平均降雨量在1 049.3~1 145.1 mm之间，最大日降雨量达199 mm。滑坡监测设备平面布置如图 3所示。

图 3滑坡监测平面布置

图 4为累计降雨和JC08点位的位移监测数据叠加图。由图 4可知，滑坡降雨主要集中在4—8月，7月达到降雨峰值，降雨量增加，降雨达到一定强度时，滑坡出现拐点，累计位移分层进入另一阶段，滑坡变形速率也明显增大；当降雨量少时，累计位移曲线呈平缓上升趋势，总体呈阶梯状。

图 4累计位移与降雨关系

本文选取该滑坡2015年7月13日—2018年12月20日的数据进行分析、建模，其中包括雨量数据，JC08及其邻近监测点位(JC02、JC05)的形变监测数据。原始数据共1285条，2015年7月14日作为初始条件，训练集为2015年7月15日—2018年11月20日数据，测试集为2018年11月20日—2018年12月20日数据。

2.2 滑坡位移分解及趋势项预测

根据式(2)，选取n=10 d为移动平均周期提取后趋势项，为避免采用相同时序数据进行预测，将JC02、JC05、JC08监测点位累计位移曲线向前滚动3 d，趋势项和邻近监测点位累计位移可视化分析，如图 5所示。

图 5趋势项与JC02、JC05、JC08关系

由图 5(a)可看出，累计位移趋势项和向前推移3 d的邻近点位累计位移(JC02、JC05)具有相同的阶梯型趋势，图 5(b)中趋势项和3个累计位移点具有强正相关性，位移在时间轴上呈逐渐上升趋势。鉴于此特性，本文采用多项式回归建模预测趋势项，拟合回归公式为

(

4)

式中，a、b、c、d为多项式系数；Tt为JC08累计位移趋势项；X_JC02、X_JC05、X_JC08分别为JC02、JC05、JC08向前推移3 d的监测点累计位移值。

采用训练集数据进行多项式回归建模，利用测试集数据进行预测，回归结果如表 1、图 6所示。表 1中MSE(mean squared error)为平均均方误差。

表 1 JC08趋势项回归

图 6JC08趋势项预测

2.3 周期项预测

在分解获得周期项时，将周期项与日降雨量依时间度量进行可视化，如图 7所示。

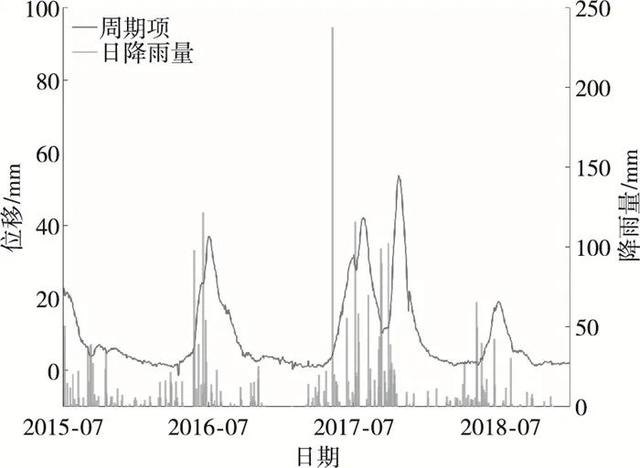
图 7JC08周期项

由图 7可知，JC08周期项波动较大，在日降雨量聚集处发生激增，且具有一定的滞后性；而日降雨量稳定后，周期项趋于平稳，上述现象呈明显的周期函数态势。为进一步分析周期项与降雨量的相关性，依据滑坡累计位移加速度将滑坡变形分为4个阶段：初始变形阶段、等速变形阶段、加速变形阶段和临滑阶段^[18]。考虑本文滑坡工况，2015年7月—2017年10月具有明显的位移加速度变化和分层，因此，根据平均加速度以4个月为一个周期，将该时序分为3个阶段(初始变形阶段：2015年7月—2016年6月；等速变形阶段：2016年7月—2017年6月；加速变形阶段：2017年7月—2017年10月)，用于评价周期项与不同时序前期累计降雨量(10、15、30、45、60 d)的相关性。同时，考虑滑坡是非线性的复杂动力学过程^[19]，通过非参数统计方法——斯皮尔曼(Spearman)秩相关系数作为不同阶段的前期累计降雨因子与周期项相关性评价依据。Spearman秩相关系数计算公式为

(

5)

(

6)

式中，di为被观测两变量降序的排列序数差；xi为被观测变量的降序的排列序号；ρ为Spearman秩相关系数；m为样本个数。

将上述不同阶段的前期累计降雨因子与周期项进行Spearman秩相关系数计算，结果见表 2。

表 2 降雨因子与周期项的Spearman秩相关系数

由表 2可知，加速变形阶段的降雨因子与周期项相关性明显发生变化，不同阶段的降雨因子与周期项相关性存在差异，且随着滑坡累计位移加速度的增加，两者相关性逐渐增加；同时，不同阶段的周期项与不同时序的前期累计降雨量的相关性存在差异性。

基于上述分析，将注意力机制引入预测模型，对不同阶段的前期降雨量因子进行注意力分布学习，自动发掘不同阶段降雨因子与周期项相关性，并解决一般LSTM预测时隐藏层共享参数导致的序列细节被忽略问题，提高滑坡位移预测模型的稳健性。

将滑坡数据的10、15、30、45、60 d前期累计降雨量作为特征变量，利用PyTorch搭建模型框架训练基于注意力机制的Bi-LSTM模型，设置基于注意力机制的Bi-LSTM模型的隐藏层数为64层，以4层隐藏层数为64层的LSTM对相同的数据进行模型训练并作精度比较，两种模型分别进行7000次Adam优化，得到JC08周期预测结果如图 8、表 3所示。

图 8JC08周期项预测

表 3 JC08周期项预测结果

由图 8看出，单纯使用LSTM未对不同时序的影响因子进行注意力分布计算，模型以全局数据无差别拟合，丢失了细节信息，预测结果在2018年12月8日后发生突变，只在短期预测表现良好，在超过临界点后误差会明显增大，而基于注意力机制的Bi-LSTM周期项预测曲线与真实值曲线大致贴合，在周期项预测过程中仍保持较好的泛化能力。同时，由表 3可知，两种模型在经过7000次训练后，其Huber Loss值相差不大，均下降至0.1以下，而两种预测方法中的MSE和平均绝对误差(mean absolute error，MAE)相差较大，表明基于注意力机制的Bi-LSTM较LSTM泛化能力更稳健。

2.4 累计位移预测及精度评定

将时间序列分解得到的趋势项和周期项分别进行建模预测，得到预测值累加，进而获取最终的位移预测值。如图 9所示，与测试集(滑坡2018年11月20日—2018年12月20日数据)进行滚动预测验证，预测值与真实值曲线大致贴合。

图 9累计位移预测

为定量评定模型预测效果，采用MAE、MSE及绝对误差衡量预测结果精度。计算得到MAE为0.088 mm，MSE为0.042 mm，且绝对误差无明显分布规律，满足预测可靠性的要求。

3 结 论

本文针对降雨型滑坡的高精度位移预测问题，深入分析影响因子与滑坡累计位移关系，首先通过时间序列将累计位移分解为周期项和趋势项，然后针对分解项分别利用模型进行位移预测，并在预测模型中引入注意力机制的思想，构建位移预测模型框架，提出基于注意力机制的Bi-LSTM降雨型滑坡预测模型。经过试验验证，得到以下主要结论：

(1) 考虑降雨型滑坡演化特性，将降雨型滑坡累计位移分解为趋势项和周期项，趋势项与不同时序邻近点位具有强正相关性，周期项和不同阶段的前期累计降雨量相关性存在差异，需要对不同阶段的影响因子和位移进行分析，以便构建更加有效的位移预测模型。

(2) 建立基于注意力机制的降雨型滑坡变形预测模型，对滑坡累计位移进行预测，注意力机制在Bi-LSTM隐藏层编码后自动挖掘不同阶段影响因子对周期项的时序相关性及关键数据，泛化能力明显优于LSTM模型，是一种稳健的降雨型滑坡位移模型。后期可对该模型进行迁移学习，增加模型的普适性，形成更有效的降雨型滑坡早期预警决策支持。

作者简介

作者简介：唐菲菲(1980—),女,博士,副教授,研究方向为地质灾害监测预警。E-mail:fftang80@126.com

初审：纪银晓

复审：宋启凡

终审：金 君

资讯

,