20道关于相似三角形的题（一道相似三角形典型小综合题）

最近天气变得阴冷，大家一定要注意保暖哦，如果感冒了真的很难受！今天，数学世界继续为大家讲解初中数学几何题，此题是一道典型的相似三角形判定与性质的小综合题，题目比较简单，对数学基础较好的学生可以说是轻而易举。请大家先思考一下，再看后面的解析过程！每个人的基础不同，希望学生能够学会相关的思考过程！

例题：（初中数学几何题）如图，在△ABC中，已知∠BAC=120°，点D、E在边BC上，且△ADE是等边三角形，求证：DE^2=BD·CE．

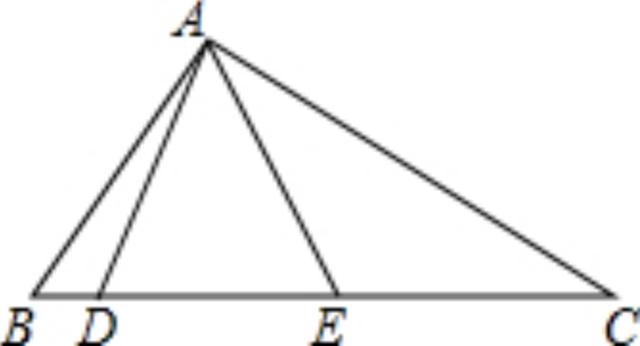
此题给出的直接条件比较笼统，需要从中提炼出有用的具体信息。由于许多学生不会进行分析，所以对于所要证明的结论是毫无头绪。解决此题的关键是灵活运用相似三角形的判定和性质，以及等边三角形的性质。下面，我们就一起来分析这道例题吧！

解析：（证明）∵△ADE是等边三角形，

∴AD=AE=DE，∠ADE=∠AED=∠DAE=60°，（根据等边三角形的性质得到）

∴∠ADB=∠AEC=120°，（等角的补角相等，并求出度数）

∵∠BAC=120°，

∴∠BAD ∠CAE=60°，（根据角的和差关系直接得出）

∵∠B ∠BAD=∠ADE=60°，（根据两个内角和等于一个不相邻的外角）

∴∠B=∠CAE，（通过等量代换即可得到）

∴△ABD∽△CAE，（相似三角形的判定）

∴AD/CE=BD/AE，（相似三角形的性质）

即AD·AE=CE·BD，

∵AD=AE=DE，

∴DE^2=BD·CE．（证毕）

温馨提示：由于此文是由原创作者猫哥一字一句打出来的，时间也比较紧，所以文中难免会出现一些小错误，还请大家谅解！另外，若朋友们还有不明白的地方或者有更好的解题方法，欢迎留言参与讨论。谢谢！