逻辑关系选择题解题技巧（语文学习中的逻辑）

一、判断

---

1、判断是一个逻辑学名词，判断这种思维方式通常表现为两个或更多概念之间的联系，当人们以判断形式确定概念之间的特定关系时，就是在进行断定。

通俗地说，判断是对思维对象是否存在、是否具有某种属性以及事物之间是否具有某种关系的肯定或否定。

判断是对思维对象有所肯定或有所否定的一种思维形式。

判断的第一个特征，就是它必须对事物的情况有所断定。

如果对事物的情况既不肯定也不否定，而只是表示疑问，那就不是判断，而只能是问题。

判断的特征之二，就是它有真假之分。

如果一个判断所断定的，是符合客观实际情况、与事实相一致的，这个判断就是真的，否则，就是假的。

检验判断真假的标准是社会实践。判断按其结构可分为简单判断和复合判断两大类。

2、语句是判断的语言表达形式。

判断是语句的思想内容，语句是判断的语言表达形式，正确运用判断进行解释，要深入理解和掌握表达判断逻辑结构的词语。只有那些对事物有断定，从而有真假可言的句子，才能表达判断。

一般来说，陈述句都表达判断。

疑问句、祈使句、感叹句不表达判断。

二、判断的结构形式

---

判断的通常结构顺序是：（量项）主项 （量项）联项 （量项）谓项。

1、主项S，简单判断中反映断定的对象的概念，可以视作句子成分的主语。

如"科学技术是生产力"中的"科学技术"，就是主项。

性质判断中的主项只有一个；

关系判断中的主项有两个或更多，分别称为前主项、后主项，或第一主项、第二主项、第三主项……

如"鲁迅和许广平是夫妻"；"鲁迅"是第一主项，"许广平"是第二主项，"夫妻"是谓项。

---

2、谓项P是主项（视作句子成分的主语）的具体描述的承载，担负着主项的性质或者关系的描述。谓项，可以视作句子成分的宾语。

“按劳分配是社会主义的分配原则”中的“分配原则”就是谓项；

“我国人民反对任何外来侵略”中的“外来侵略”也是谓项。

---

3、联项，就是连结主项和谓项的那个概念，或者说联项是表示被断定的对象和其性质间关系的那个概念。

可以视作句子成分的动词谓语。

一般来讲联项只包括“是”和“不是”两个，有时可以省略：如“金属能导电”就省略了联项。

其中，“是”是肯定联项，它表示思维对象具有某种性质；

“不是”是否定联项，它表示思维对象不具有某种性质。

所有商品都是可以用来交换的劳动产品。

任何事物都不是静止的。

---

4、量项是表示主项所指称的对象的数量语词。可以视作句子成分的修饰定语或限制状语。

量项分全称量项、特称量项、单称量项。

---

（1）全称量项，表示对主项的全部外延都作了断定：

每一个、任意一个、所有的、一切、凡……

也可以用“都”“全部”“全都”等副词、“人人”等主语重复的形式来表达，甚至有时可以没有任何的量词标志（集合名词）。

所有金属都是可以分割的。

（“全称量项”有时可以省略）人类是有智慧的。

---

（2）特称量项，表示没有对主项的全部外延作断定，“特称量项”不能省略。

有的、有些、一些、某些、少数、多数、许多、几乎全部、百分之几……（也可以用“最起码”“至少”“最少”“至多”“最多”“绝大多数”“并非所有”等副词、“一定程度上”“一定意义上”等介词结构表达）。

有的花不是红色的。

有的科学家是自学成才的。

有些闪光的不是金子。

---

（3）单称量项，表示对主项外延中的某一个特定对象作出了断定：

这、那、这些、那些等指示代词、人称代词和专有名词。

如果主项是一个单独概念，单称量项可以省略。

如果主项是一个普通概念，则不能省略。

北京是中华人民共和国首都。

爱因斯坦是犹太人。

这个三角形是等腰三角形。

地球不是恒星。

5、周延：指判断本身直接或间接地对其主项（或谓项）的全部外延作了表述的，就称这个判断的主项（或谓项）是周延的。

中项周延，指中项必须是谓项或主项的子集，这样它作为“中介”，才能保证大项与小项一定相交，即得出肯定性结论。

中项不周延是在两个前提中，中项有一部分外延同谓项有某种关系，又有一部分外延同主项有某种关系，但不能确定哪一部分外延与主项谓项必然有交集，不能有效联结主项谓项。

---

全称或单称判断的主项都周延。

所有蝙蝠都是哺乳动物。

特称判断的主项都不周延。

有些学员不是武汉人。

肯定判断的谓项都不周延。

狮子是动物。

否定判断的谓项都周延。

故意犯罪都不是过失犯罪。

性质判断类型	主项周延？	谓项周延？	量项！	联项！
A全称肯定命题	周延	不周延	全称量项 主项	肯定
E全称否定命题	周延	周延	全称量项 主项	否定
I特称肯定命题	不周延	不周延	特称量项 主项	肯定
O特称否定命题	不周延	周延	特称量项 主项	否定

---

主项S外延与谓项P外延的关系有五种：全同关系、被包含关系、包含关系、交叉关系和全异关系。

谓词逻辑中有“量词”，量词，是在命题中表示数量的词。

量词有两类：

全称量词（∀），表示“所有的”或“每一个”；

存在量词（∃），表示“存在某个”或“至少有一个”。

A全称肯定命题、E全称否定命题、I特称肯定命题、Ο特称否定命题

A命题代表：全称肯定命题，即所有S是P。

E命题代表：全称否定命题，即所有S不是P。

I命题代表：特称肯定命题，有的S是P。

O命题代表：特称否定命题，有的S不是P。

同一素材的A、E、 I、O之间存在如下真假关系：

1、矛盾关系。分司存在于A和0、E和I之间，具有矛盾关系的两个判断 ，即不能同真，也不能同假。

2、反对关系。存在于A和E之间。具有反对关系的两个判断，不能同真，可以同假。

3、下反对关系。存在于I和0之间。具有下反对关系的两个判断,不能同假，可以同真。

4、差等关系（从属关系）。分别存在于A和I、E和0之间。具有差等关系的两个判断，一个是全称判断，一个是特称判断。

具有差等关系的两个判断之间具有如下的真假关系：

如果全称判断是真的，则特称判断也是真的；

如果全称判断是假的，则特称判断真假不定；

如果特称判断是真的，则全称判断真假不定；

如果特称判断是假的，则全称判断也是假的。

---

---

三、判断类型

---

判断是对思维对象有所肯定或有所否定的一种思维形式。

分类：直言判断、联言判断、选言判断、假言判断、负判断、模态判断

---

（一）直言判断

---

1、直言判断：是断定事物具有或不具有某种性质的简单判断，也叫性质判断。

直言判断由主项、谓项、量项、联项四部分构成 。

在分析直言判断形式时，通常用S和P分别表示主、谓项。

量项分为全称量项(“所有” 、“任一”，…) 和特称量项(“有的”、“一些”，…) ；

联项分为肯定联项(“是”) 和否定联项(“不是”) 。

(1) 所有的金属都是导电的。

(2）所有犯罪者都不是守法公民。

(3) 有的天鹅不是白的。

---

2、直言判断分为四种基本类型

全称（含单称）肯定判断SAP，简称A判断，

标准形式是“所有S都是P”。如上例(1) 所有的金属都是导电的。

全称（含单称）否定判断SEP，简称E判断，

标准形式是“所有S都不是P”。如：“所有宗教都不是科学。 ”

特称肯定判断SIP，简称I判断，

标准形式是“有的S是P”。例如：“有的哺乳动物是卵生的|胎生的。”

特称否定判断SOP，简称O判断，

标准形式是“有的S不是P”。如上例(3) 有的天鹅不是白的。

---

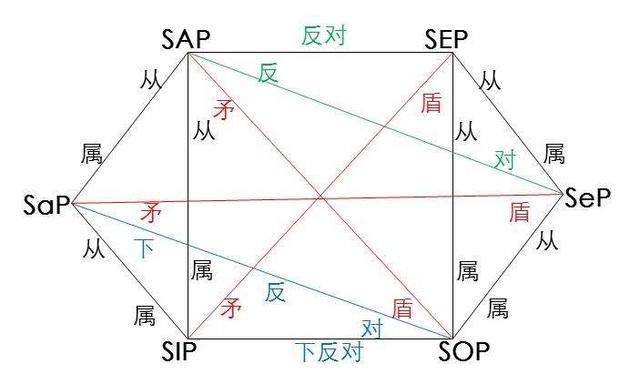
3、直言判断的对当关系：逻辑方阵

传统逻辑用来表示具有相同素材(即主项和谓项分别相同)的A(全称肯定命题)、E(全称否定命题)、I(特称肯定命题)、O(特称否定命题)四种命题形式之间的真假制约关系的图式。

---

（1）矛盾关系，即A与O、E与I这两对命题形式之间的关系:二者既不能同真，也不能同假。

根据这一关系，如果我们知道A判断是真的，就可以断定O判断是假的；

如果知道E判断是真的，就可以断定I判断是假的。

同样，如果知道A、E、I、O判断是假的，也就可以断定对应的O、I、E、A判断是真的。

（2）反对关系（上反对关系），即A与E这两种命题形式之间的关系:二者不能同真，即一个真，另一个必假；但二者可以同假，即当一个假时，另一个可真可假。

这是A判断和E判断之间的关系。它们是不能同真，可以同假的关系。在A、E两个判断中，如果我们知道其中一个是真的，就可推知另一个是假的。

例如：已知A：科学技术都是生产力。(真)

则 E：科学技术不都是生产力。(假)

已知E：所有的科学家都不是思想懒汉。(真)

则 A：所有的科学家都是思想懒汉。(假)

如果我们知道其中一个是假的， 那么另一个真假不定。

例如：已知A：我们班同学都是姓李。(假)

则 E：我们班同学都不姓李。(真假不定)

(3)下反对关系，即I与O这两种命题形式之间的关系:二者不能同假，即一个假时，另一个必真；但二者可以同真，即当一个真时，另一个可真可假。

这是I判断和O判断之间的关系，它们是可以同真但不能同假的关系。在I、O两个判断中，如果我们知道其中一个是假的，那就可以断定另一个是真的。

例如：已知I：有些民主人士是共产党员。(假)

则O：有些民主人士不是共产党员。(真)

已知O：有些机器不需要能源。(假)

则I：有些机器需要能源。(真)

如果我们知道其中一个是真的，那么另一个真假不定。

例如：已知I：有些个体户纳税了。(真)

则O：有些个体户没纳税。(真假不定)

（4）差等关系(从属关系），即A与I、E与O这两对命题形式之间的关系:全称命题真，特称命题必真；

全称命题假，特称命题真假不定;特称命题真，全称命题真假不定;特称命题假，全称命题必假。

这是A判断和I判断之间、E判断和O判断之间的关系。

注意到从属关系存在于一个全称判断与一个特称判断之间。我们可以这样概括这一关系：

如果全称判断真，则相应的特称判断真；

如果特称判断假，则相应的全称判断假；

如果全称判断假，则相应的特称判断真假不定；

如果特称判断真，则相应的全称判断真假不定。

---

4、一般把单称命题作为全称命题的特例来处理。

但是，在考虑对当关系(即真假关系)时，单称命题不能作为全称命题的特例。

如果涉及有同一素材的单称命题，那么以上所述的对当关系要稍加扩展：

单称肯定命题和单称否定命题是矛盾关系；

全称命题与同质的单称命题是差等关系；

单称命题与同质的特称命题也是差等关系。

把单称命题考虑其中，所有对当关系可用下图来表示：

---

（二）关系判断

---

1、关系判断：断定事物和事物之间的关系的简单判断。由主项、谓项和量项组成。

关系判断由三部分构成：

（1）、关系者项。表示一定关系的承担者的概念，也就是关系判断的主项。

（2）、关系项。表示关系者之间存在的关系的概念，也就是关系判断的谓项。

存在于两个对象之间的关系称为二元关系，存在于三个对象之间的关系称为三元关系，存在于n个对象之间的关系是n元关系。

（3）、量项。表示关系者项数量的概念，包括全称、特称或者单称，如“所有的”“某些”……。

如果关系者项是单独概念，就不使用量项。如：小张和小李是同学。

关系判断的逻辑形式是R(A、B、C......n)

其中A、B、C等表示关系主项，R表示关系，n表示主项的数目。

---

2、对称性关系

（1）对称关系

对称关系存在于两个或两类事物之间。在两个或两类事物之间，如果甲事物对乙事物有某种关系，乙事物对甲事物肯定也具有同样的关系。那么二者之间的关系叫对称关系。

如：甲和乙是同乡，乙和甲当然也是同乡，同乡关系就是对称关系。

（2）反对称关系

如果甲事物对乙事物有某种关系，而乙事物对甲事物肯定不具有这种关系。那么二者之间的关系叫反对称关系。(大于、小于、多于、少于、之前、之后、高于、低于、早于、晚于等等)

如：五大于三，而三肯定不能再大于五，大于关系就是反对称关系。

（3）半对称关系

如果甲事物对乙事物具有某种关系，而乙事物对甲事物可能具有、也可能不具有这种关系。那么二者之间的关系叫半对称关系。

如：甲喜欢乙，乙可能喜欢甲，也可能不喜欢甲，“喜欢”就是半对称关系。

3、传递性关系：

（1） 传递关系

如果甲事物与乙事物具有某种关系，乙事物与丙事物也具有这种关系，而甲事物与丙事物同样具有此种关系，那么三者之间的这种关系就叫传递关系。

如：篮球大于排球，排球大于乒乓球，则篮球大于乒乓球。这种大于关系就是传递关系。

（2）反传递关系

如果甲事物对乙事物具有某种关系，乙事物对丙事物也有这种关系，而甲事物与丙事物肯定不具有此种关系，那么三者之间的这种关系就叫反传递关系。

如：甲是乙的父亲，乙是丙的父亲，那么甲肯定不是丙的父亲，这就是反传递关系。

（3）半传递关系

如果甲事物对乙事物具有某种关系，乙事物对丙事物也有这种关系，而甲事物与丙事物可能有、也可能没有这种关系，那么三者之间的这种关系就叫做半传递关系。

如：甲认识乙，乙认识丙，则甲可能认识丙、也可能不认识丙，三者间的这种认识关系是半传递关系。

4、自返性关系：

（1）自返关系

自返关系是事物与其自身发生的某种关系。

如：他自杀了。自杀行为的施动者是他自己，受动者也是他自己。

（2）非自返关系

所谓非自返关系是自身和自身不能发生的关系。

如：压迫、剥削、专政、侵略等行为都是非自返关系。

,