趣味数学倒计时30天（从纯循环小数和无穷级数的角度证明）

一个数的小数部分从某一位起，一个或几个数字依次重复出现的无限小数叫循环小数（circulating decimal）。循环小数会有循环节（循环点），并且可以化为分数。

1.1 纯循环小数

从小数部分第一位开始的 循环小数 ，称为纯循环小数。纯循环小数是从十分位开始循环的小数，如0.33333333...(1/3)，0.1428571428571....(1/7)等。

将纯循环小数改写成分数，分子是一个循环节的数字组成的数；分母各位数字都是9，9的个数与循环节中的数字的个数相同.

例如：0.111...=1/9、0.12341234...=1234/9999等。

1.2 混循环

循环节不是从小数部分第一位开始的，叫混循环小数 。例如：1.2333333……、13.0984343434343……等。我们可以观察到：1.2333333……的循环节在3上面。

一个混循环小数的小数部分可以化成分数：

这个分数的分子是第二个循环节以前的小数部分组成的数与小数部分中不循环部分组成的数的差。

分母的头几位数是9，末几位是0。其中9的个数与循环节中的位数相同，0的个数与不循环部分的位数相同。

2.5 用极限（无穷级数）

等比数列的求和公式是[a1(1-q^n)]/(1-q)，那么当q<1且n->无穷大的时候，这个式子的极限就是a1/(1-q)。

由于循环小数

0.aaaaaaaaa……=a/10 a/100 a/1000 a/10000 ……，

它的每一个加数刚好构成一个无穷的等比数列，而且q=1/10，那么就可以用a1/(1-q)计算0.99999999……，

此时a1=0.9，q=1/10，

很容易就可以得到

0.9999999999……=0.9/(1-1/10)=1

或者：

0.999999…… = 1 – 0.000…..1 =

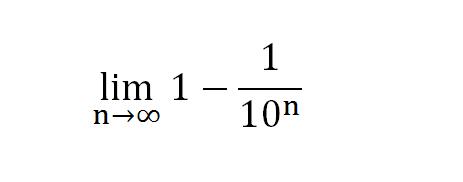
=1

当然，关键是要理解0.999999……后的省略号……，就是说，0.999999……是无限越近1，也就是极限是1，也就是上面的极限表达式，1/(10^n)的极限就是0，或者说0.0000000000……1就是0。极限是微积分的基础。

－End－