初中数学数形结合动点问题（数形结合话数轴）

数学是研究“数”和“形”的一门学科，从古希腊时期起，人们就已试图把它们统一起来。

在日常生活中，我们通常对有形的东西认识比较快，而对抽象的东西认识比较慢，这正是现阶段数学学习的特点，“以形助数”是数学学习的一个重要方法。

运用数形结合思想解题的关键是建立数与形之间的联系，现阶段数轴是数形结合的有力工具，主要反映在：

1.利用数轴形象地表示有理数；

2.利用数轴直观地解释相反数；

3.利用数轴解决与绝对值有关的问题；

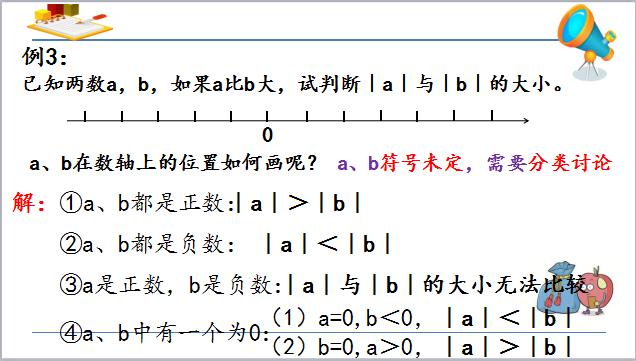
4.利用数轴比较有理数的大小。

下面通过6个例题，带领大家一起领略“利用‘数轴’，运用‘数形结合’思想解题”的独特魅力。

①分类讨论法：在解有些数学问题时，常常会出现答案不唯一或分多种情况的问题，解这类问题时，需要把所有可能情况按照一定标准分成若干类，然后逐步讨论，得出结果，这种解题方法称为分类讨论法。

②从文字、图形、图表获取信息是信息社会的基本要求。

③质点在数轴上运动，使点表示的有理数、线段的长、分类讨论、建立方程等知识方法有机融合在一起，使问题呈现动态之美。

④许多人误以为学习数学等同于了解定理的证明、背诵及套用公式、熟读例题及操练习题。其实，数学既是一门抽象的学科，亦与生活息息相关；它既是理性的追求，又是充满美感的。

例6以油条制作过程为背景，将线段的“等分点、对称、平移”等知识融入其中，有效考查了阅读理解、分析转化、数形结合等思想方法。

结束语：亲爱的同学们，学习数学可能比较枯燥，也会遇到很多困难，但是大家一定要坚持，循序渐进，日积月累，必定会有所收获。

下面把罗赛蒂的一种小诗送给大家：《我想试一试》

那个说“我想试试”

的小孩

他将登上山巅

那个说“我不成”的

小孩

在山下停步不前

“我想试试”

每天办成很多事

“我不成”

就真的一事无成

因此你务必说“我想试试”

将“我不成”弃于尘埃