浮点数1为什么变成0（看不见的浮点数）

说到浮点误差，有一个比较高深的计算机概念——浮点数，有兴趣的同学可以问度娘。简单说，在计算机的计算中，只能存储和处理二进制数据，就是1和0。excel在计算时，首先要把十进制的数值转换为二进制，交给计算机处理，最后再把二进制的结果转换为十进制，显示到Excel中。

十进制数值转换为二进制数值的计算过程为：

1、整数部分：

连续用该整数除以2取余数，然后用商再除以2，直到商等于0为止，最后把各个余数按相反的顺序排列。

如果将十进制数值22转换为二进制数值，其计算步骤如下：

22除以2结果为11，余数为0。

11除以2结果为5，余数为1。

5除以2结果为2，余数为1。

2除以2结果为1，余数为0。

1除以2结果为0，余数为1。

最后将余数按相反的顺序排列，整数22的二进制结果为10110。

2、小数部分：

用2乘以十进制小数，将得到的整数部分取出，再用2乘以余下的小数部分，然后再将积的整数部分取出。如此往复，直到积中的小数部分为0或者达到所要求的精度为止，最后把取出的整数部分按顺序排列。

如果将十进制数值0.8125转换为二进制数值，其计算步骤是：

首先用0.8125乘以2等于1.625，取整结果为1，小数部分是0.625。

0.625乘以2等于1.25，取整结果为1，小数部分是0.25。

0.25乘以2等于0.5，取整结果为0，小数部分是0.5。

0.5乘以2等于1.0，取整结果为1，小数部分是0，计算结束。

将乘积的取整结果顺序排列，结果就是0.1101。

3、整数和小数混合数值：

含有小数的十进制数转换成二进制时，先将整数、小数部分分别进行转换，然后将转换结果相加。

但是这种转换有时候会陷入无限循环，比如按照上述方法将小数0.6转换为二进制代码，计算结果就是：

0.10011001100110011……

其中的0011部分会无限重复，无法用有限的空间量来表示。当结果超出Excel计算精度，产生了一个因太小而无法表示的数字时，在Excel中的处理结果就是0。

所以在不同进制之间转换时，就很容易出现一些非常细小的误差，这就是浮点误差，

Excel里的浮点由于函数机制等原因，在某些极端情况下隐蔽性很高，所以我再写篇文章介绍下这个坑。

1，计算时产生的大量小数位数

这个结果出现大量小数位数的原因在之前的文章里已经介绍得很详细了，这里不再赘述。

2，无法录入的数据

由于浮点的问题，有些特殊数录入就能生成浮点，导致无法录入正确内容，32768.598有兴趣你就试试在excel里录入这个数。

然而这两种浮点数，在把小数位数调高后都很容易发现异常，因此稍微对Excel有一定了解的伙伴都会知道用ROUND函数修正精度，但是，Excel里存在一类更危险的的浮点数。

截图为目前这类数里目前测试下最简单的算式。0.1 0.2，无论如何调高小数位数还是显示为0.3，使用公式求值或者F9抹黑算式检查也不会出现大量小数位数，均为0.3。等号判断下和直接键入的0.3也是相同的。

但是，如果你把这个算式用于MATCH等函数内，结果却是报错的……

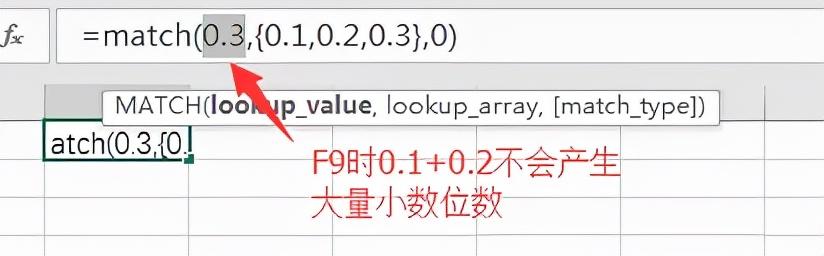
因为对Excel来说，浮点精度是可以超过15位的，可以视为高精度的浮点误差

百度后发现JS里0.1 0.2就是典型浮点误差结果为：

0.30000000000000004

由于Excel有15位精度限制，故只显示出0.3，因为15位下剩余小数位数均为0未显示出来，因此，这个性质说明Excel的浮点精度是可以高于15位的。

在实际测试中，发现部分函数能识别这种高于15位的精度差异，而且这种差异会影响公式结果，这些函数包括：

RANK、FREQUENCY、MATCH、MODE、VLOOKUP、MODE.MULT、HLOOKUP、LOOKUP

有好多同学已经被类似0.1 0.2这种不产生大量小数位数的浮点误差坑过，因为使用F9或者等号检测时都无法检测出这种高于15位的精度差异。

看到这里肯定有人会问，有没有什么函数能直接识别这种精度差？

答案是当然有，有个DELTA函数专门判断参数是不是相等的，可以识别出来，这个函数的结果为1，说明参数完全相等，为0则说明是有差异的：

除了使用ROUND修正精度的方式外，有时候我们也可以使用像COUNTIF这种不识别高于15位的精度的函数来解决这类数值的匹配问题，因为COUNTIF的第二参数在没有无比较运算符和通配符等时，会将数字全部识别为数值型统计且不会识别高于15位的精度。

好了，今天咱们的内容就是这些吧，祝各位小伙伴一天好心情！

图文制作：流浪铁匠

,