中考必考的几何模型（中考专题新初三必看）

【中考专题】新初三必看~中考几何常见模型图及结论

中考专题模型

8字模型与飞镖模型

模型1 角的8字模型

条件：AC、BD相交于点O,连接AD、BC.

结论：∠A ∠D=∠B ∠C.

---

小结：(1)因为这个图形像数字8，所以我们把这个模型称之为8字模型.

(2)8字模型往往在几何综合题中推导角度时用到.

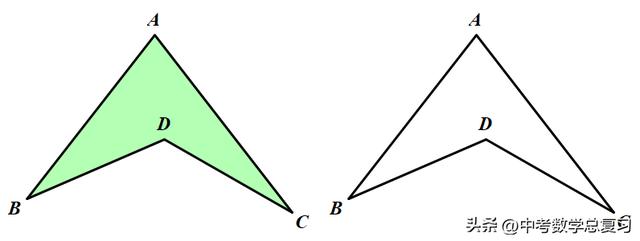
模型2 角的飞镖模型

如图所示

结论：∠D=∠A ∠B ∠C.

小结：(1)因为这个图形像飞镖，所以我们把这个模型称之为飞镖模型.

(2)飞镖模型往往在几何综合题中推导角度时用到.

模型3 边的8字模型

条件：如图所示，AC, BD相交于点O,连接AD、BC.

结论：AC BD>AD BC.

模型4 边的飞镖模型

如图所示

结论：AB AC=BD CD.

角平分线模型

模型1 角平分线上的点向两边作垂线

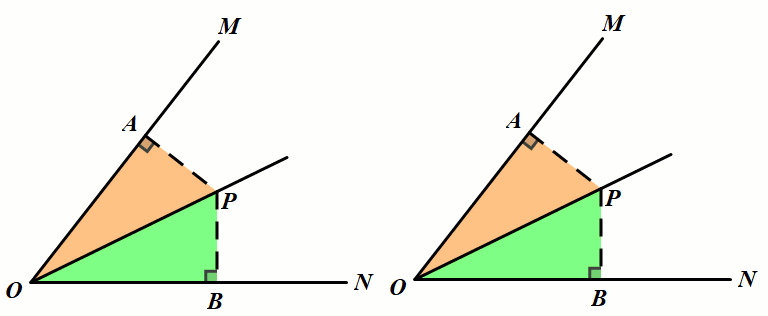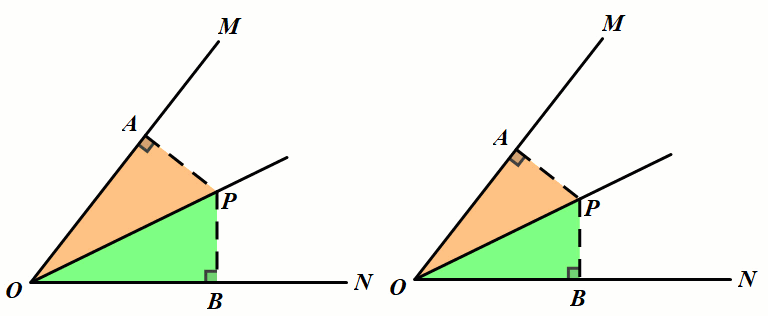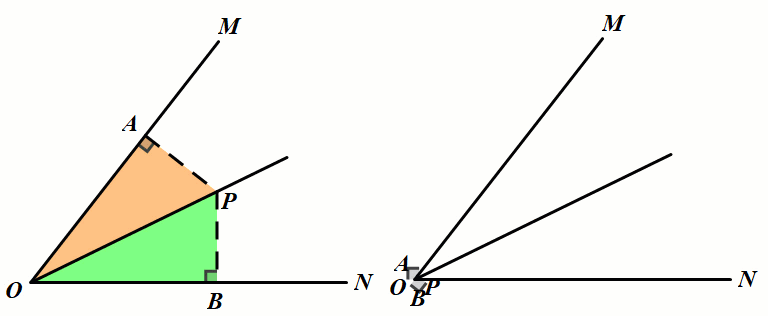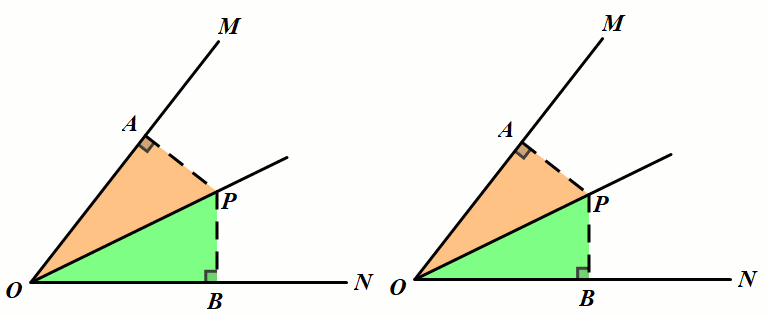
条件：如图，P是∠MON的平分线上一点，过点F作PA⊥OM于点A, PB⊥ON于点B.

结论：PB=PA.

---

小结：利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口.

模型2 截取构造对称全等

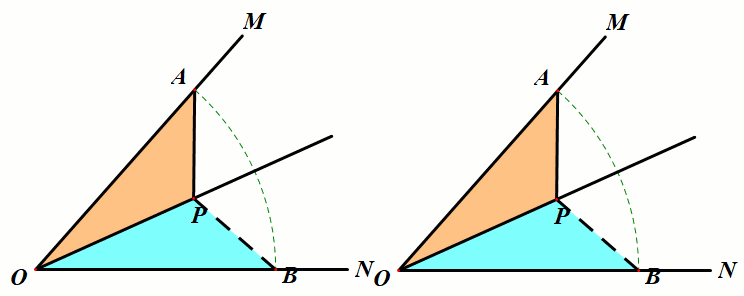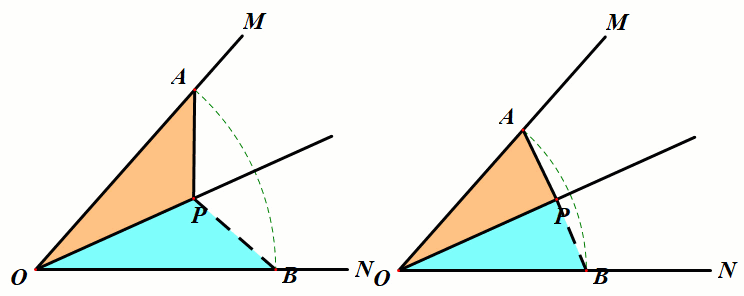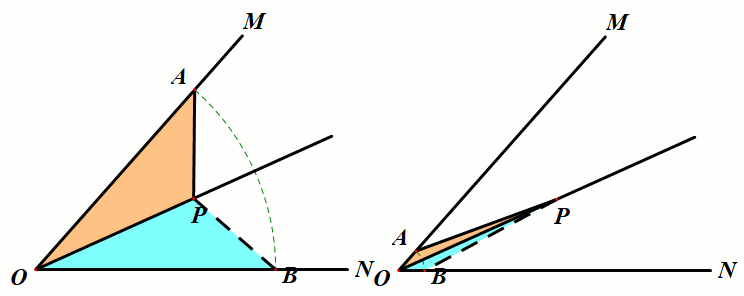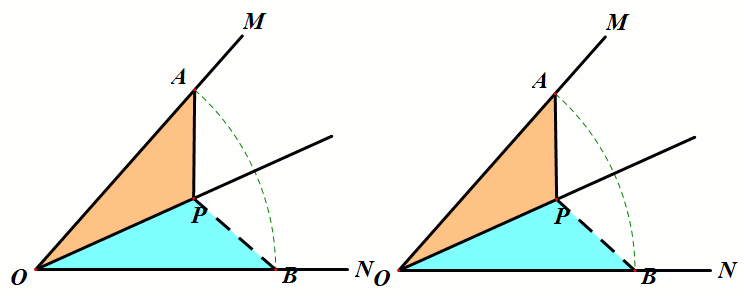
条件：如图，P是∠MON的平分线上一点，点A是射线OM上任意一点，在ON上截取OB=OA，连接PB.

结论：△OPB≅△OPA.

---

小结：利用角平分线图形的对称性，在角的两边构造对称全等三角，可以得到对应边、对应角相等.利用对称性把一些线段或角进行转移，这是经常使用的一种解题技巧.

模型3 角平分线 垂线构造等腰三角形

条件：如图，P是∠MON的平分线上一点，AP⊥OP于P点,延长AP交ON于点B.

结论：△AOB是等腰三角形.

---

小结：构造此模型可以利用等腰三角形的“三线合一”，也可以得到两个全等的直角三角形，进

而得到对应边、对应角相等.这个模型巧妙地把角平分线和三线合一联系在一起.

模型4 角平分线 平行线=等腰三角形

条件：如图，P是∠MON的平分线上一点，过点P作

PQ//ON,交OM于点Q,

总结：△POQ是等腰三角形.

小结：有角平分线时，常过角平分线上一点作角的一边的平行线，构造等腰三角形，为证明结

论提供更多的条件，体现了角平分线与等腰三角形之间的密切关系.

双角平分线模型

模型1 “内内”双角平分线模型

条件：BP、CP为角平分线.

结论：∠BPC=90° 1/2∠A.

模型2 “外外”双角平分线模型

条件：BP、CP为角平分线.

结论：∠BPC=90°-1/2 ∠A.

模型3 “内外”双角平分线模型

条件：BP、CP为角平分线.

结论：∠BPC=1/2 ∠A.

模型4 “8字型”下的双角平分线模型

条件：BP、CP为角平分线.

结论：∠P= (∠A ∠D).

模型5 同旁内角的双角平分线模型

条件：BO、AO为角平分线，CD⊥AB，AD∥BC.

结论：∠AOB=90°,OD=OC,AB=AD BC.

模型6 凹四边形的双角平分线模型

条件：BE、DE为角平分线，BE交AD于点G.

结论：∠E= (∠A-∠C).

截长补短模型

模型：截长补短

如图①，若证明线段AB、CD、EF之间存在

EF=AB CD,可以考虑截长补短法.

截长法：如图②，在EF上截取EG=AB,再证明

GF=CD即可.

补短法：如图③，延长至H点，使BH=CD,

再证明AH=EF即可.

手拉手全等模型

模型1 一般等腰三角形

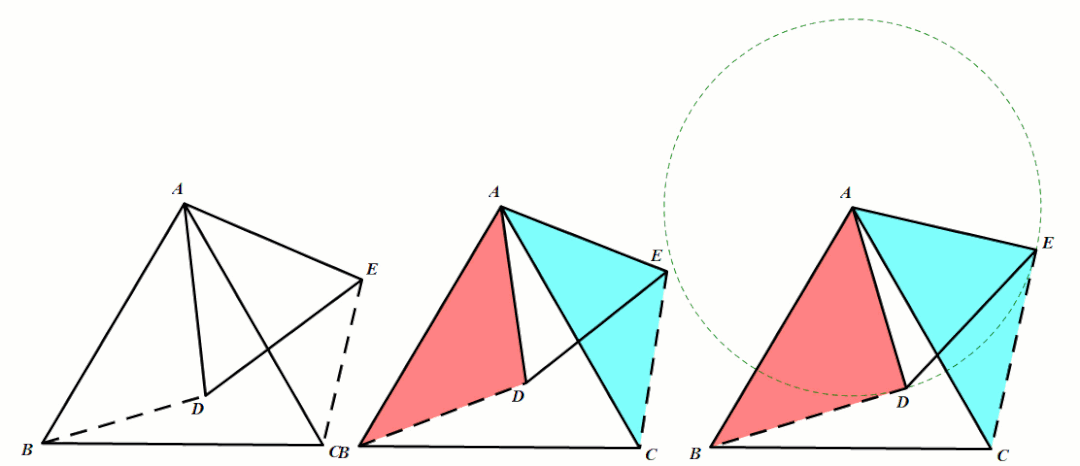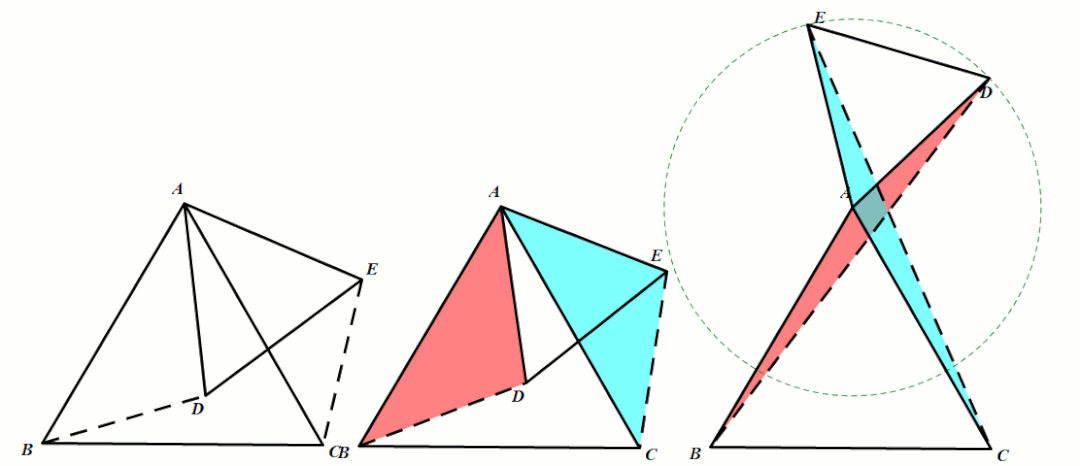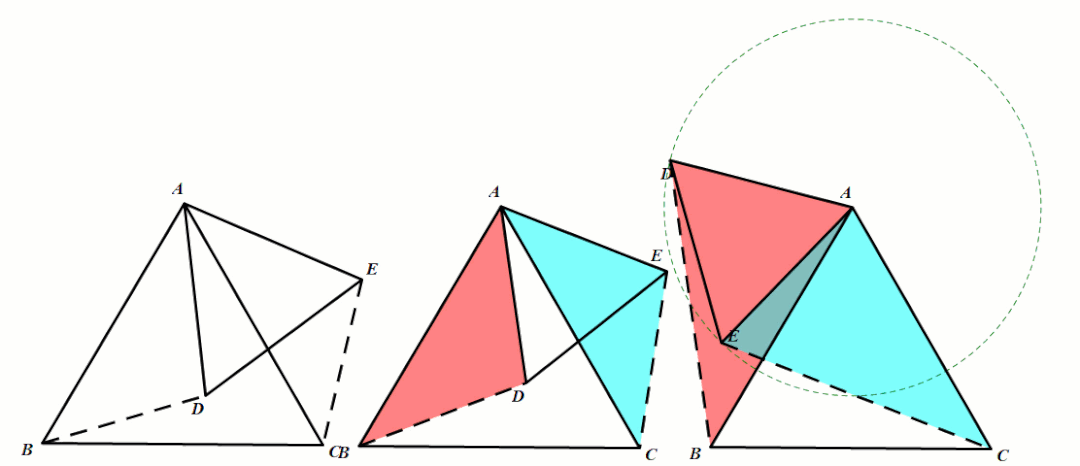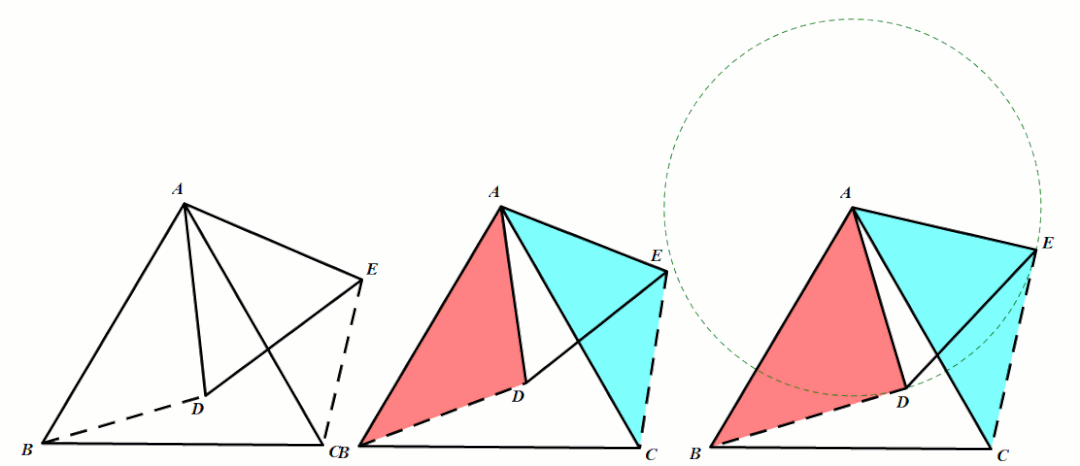
条件：AB=AC,AD=AE,∠BAC=∠DAE.

结论1：△ABD≅△ACE.

---

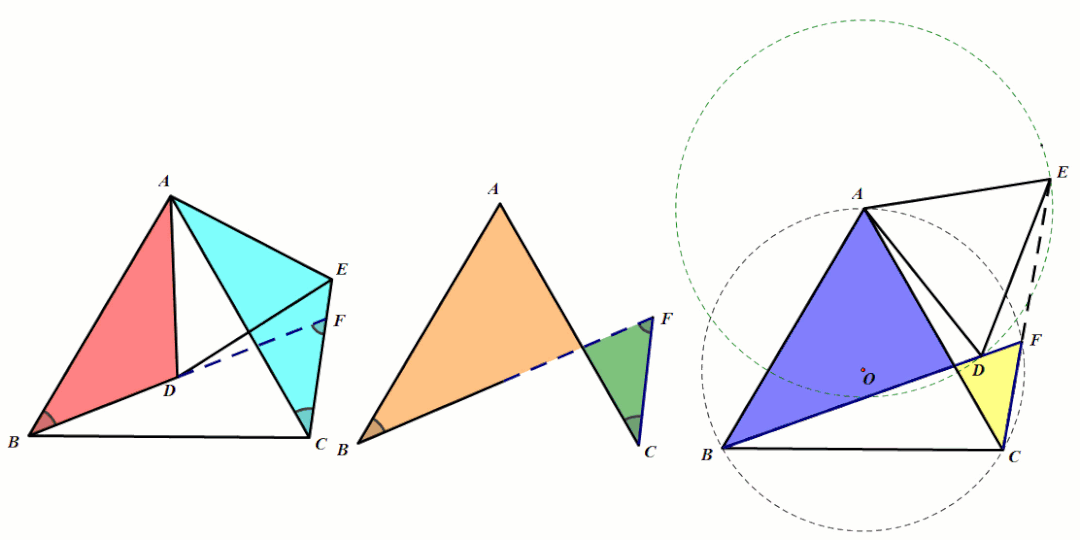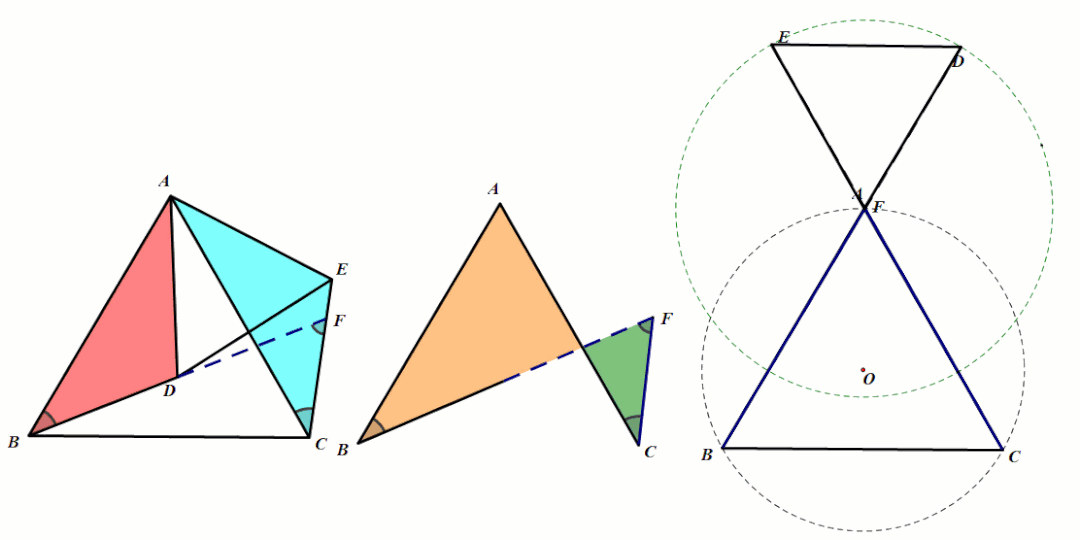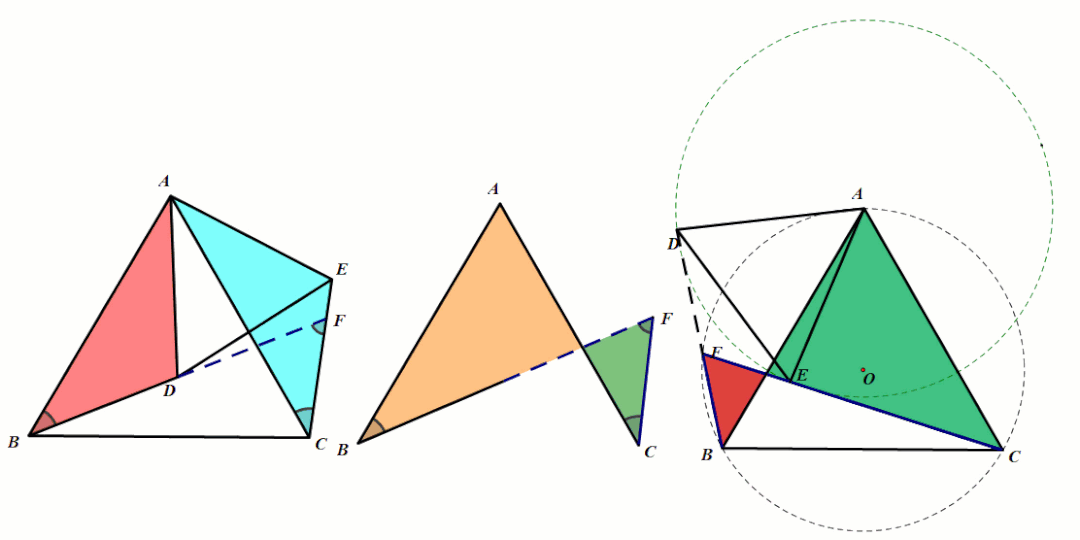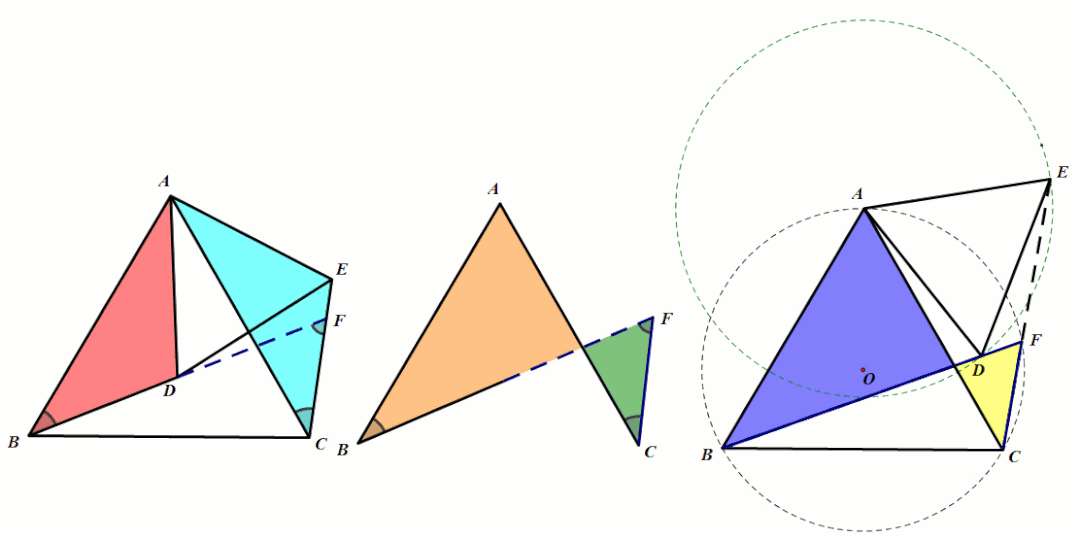
条件：等腰△ABC和等腰△ADE,∠BAC=∠DAE（顶角相等）.

结论2：第三边所成的夹角∠BFC=∠BAC（8字型模型可推出）且四点共圆.

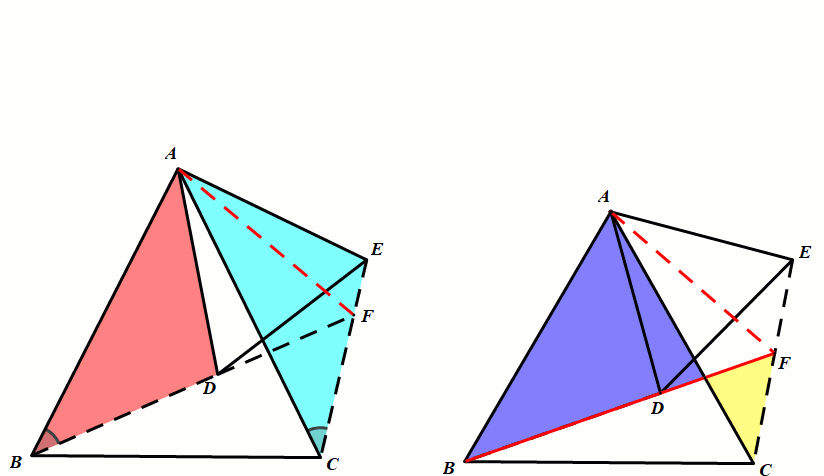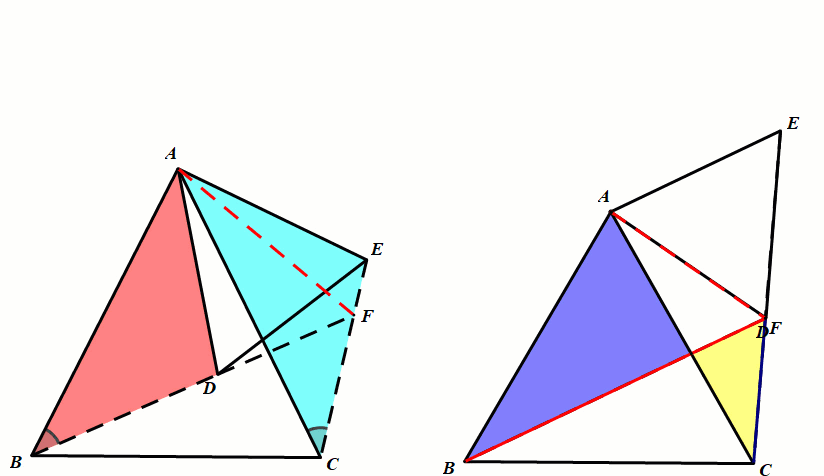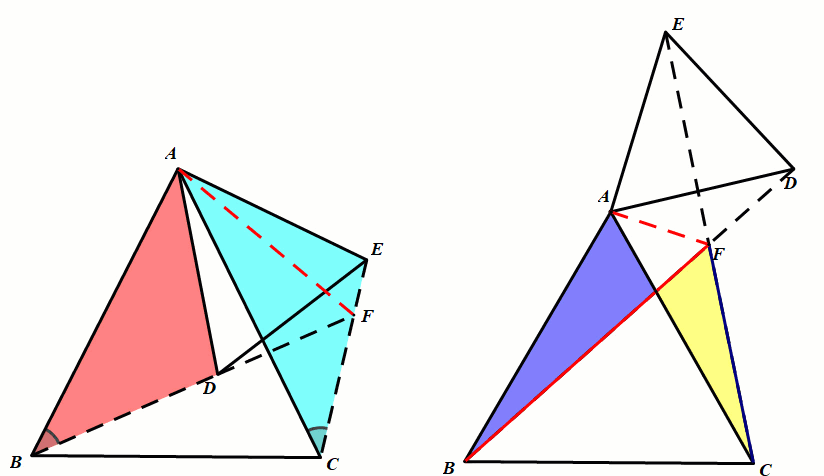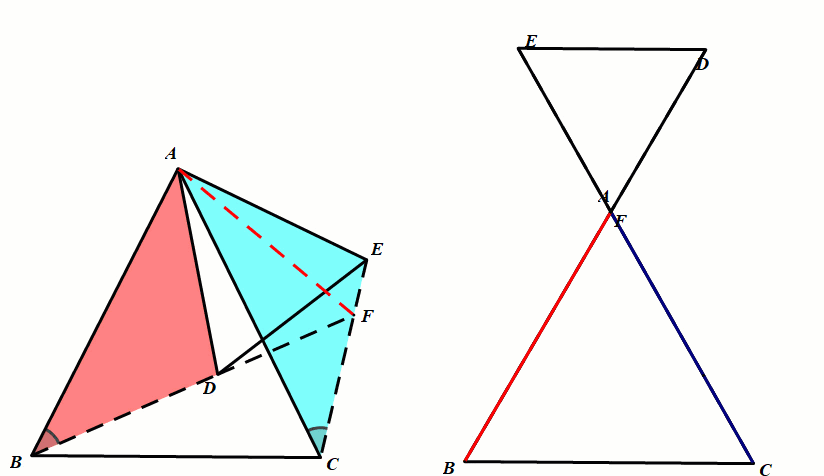
条件：等腰△ABC和等腰△ADE,∠BAC=∠DAE（顶角相等）.

结论3：FA平分∠BFE.（利用面积法以及角的平分线的判定定理）.

条件：等腰△ABC和等腰△ADE,∠BAC=∠DAE（顶角相等），P、Q分别为BD、CE的中点.

结论4：△APQ是等腰三角形.

条件：等腰△ABC和等腰△ADE,∠BAC=∠DAE（顶角相等），点B、D、E三点共线时

结论5：A、B、C、E四点共线.

条件：等腰△ABC和等腰△ADE,∠BAC=∠DAE（顶角相等），点D在BC上运动.

结论6：四边形ADCE是对角互补且邻边相等的共圆四边形，CA平分∠DCE.

模型2 等边三角形手拉手旋转

条件：△OAB，△OCD为等边三角形

结论：△OAC≅△OBD,

第三边的夹角∠AEB=60°,EO平分∠AED

四边形OABE对角互补,

四边形OCED对角互补、邻边相等、角平分线、60°的结论.

模型3 等腰直角三角形手拉手旋转

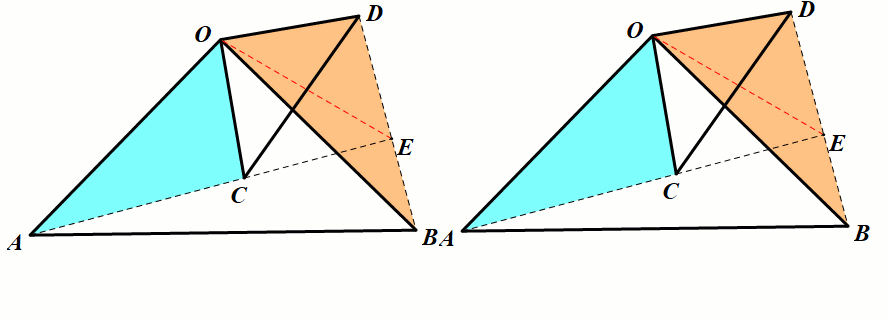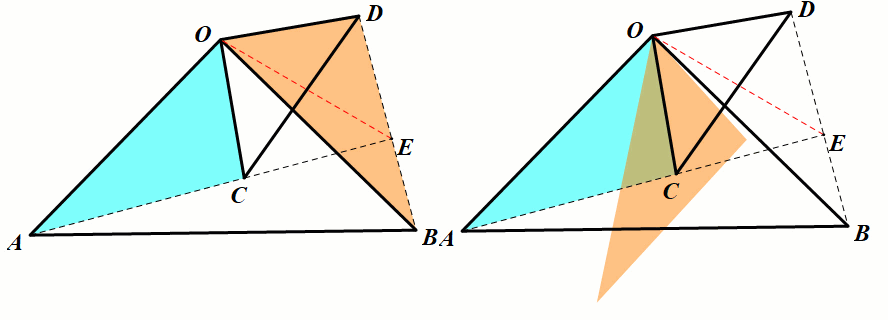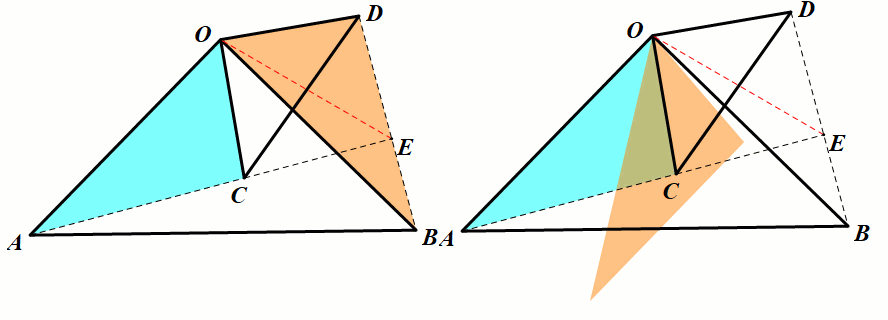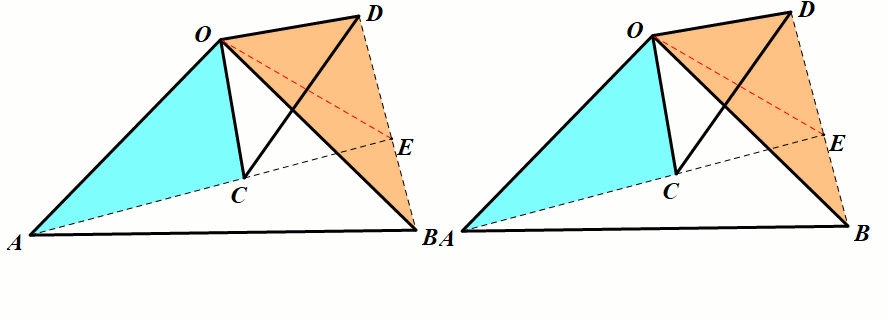
条件：△OAB，△OCD为等 腰直角三角形

结论：△OAC≅△OBD,

第三边的夹角∠AEB=90°,EO平分∠AED.

正多边形中的全等模型

模型1 等边三角形中的全等

条件：等边△ABC，BD=CE.

结论：△ABD≅△BCE;∠AFE=60°.

总结：等边三角形中的全等，第三边所成的夹角等于60°.

---

模型2 正方形中的全等

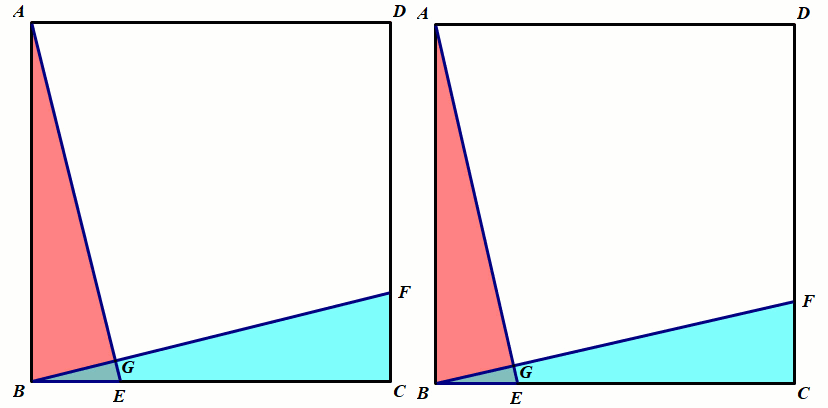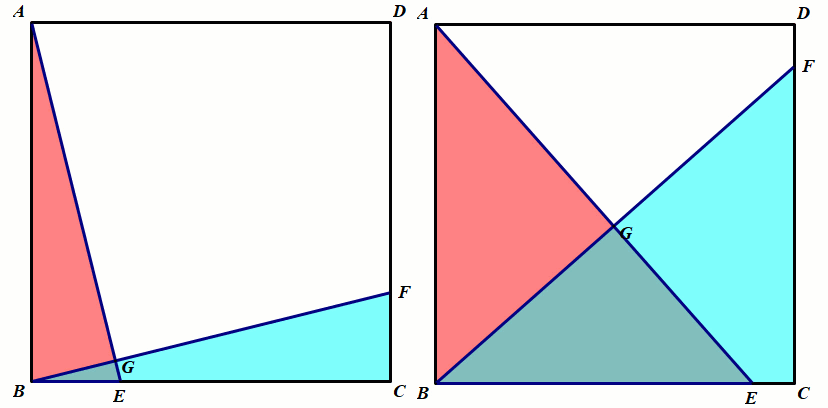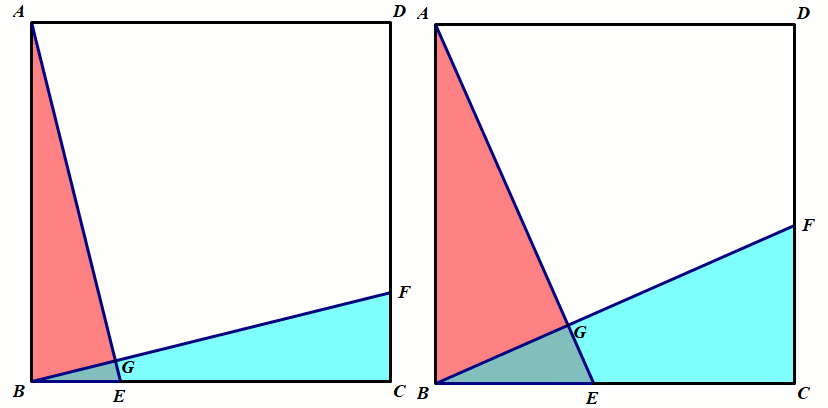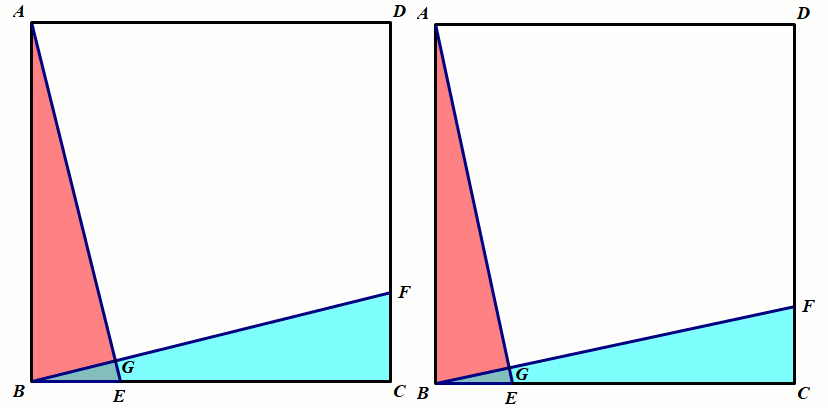
条件：正方形ABCD，BE=CF.

结论：△ABE≅△BCF;∠AGF=90°.

总结：正方形中的全等，第三边所成的夹角等于90°.

---

模型3 正五边形中的全等

条件：正五形ABCDE，BF=CG.

结论：△ABF≅△BCG;∠AHG=108°.

总结：正五边形中的全等，第三边所成的夹角等于108°.

一线三等角全等模型

模型1 同侧一线三等角

已知：∠B=∠C=∠AED,AE=DE.

结论：△ABE≅△ECD.

---

模型1 同侧一线三等角

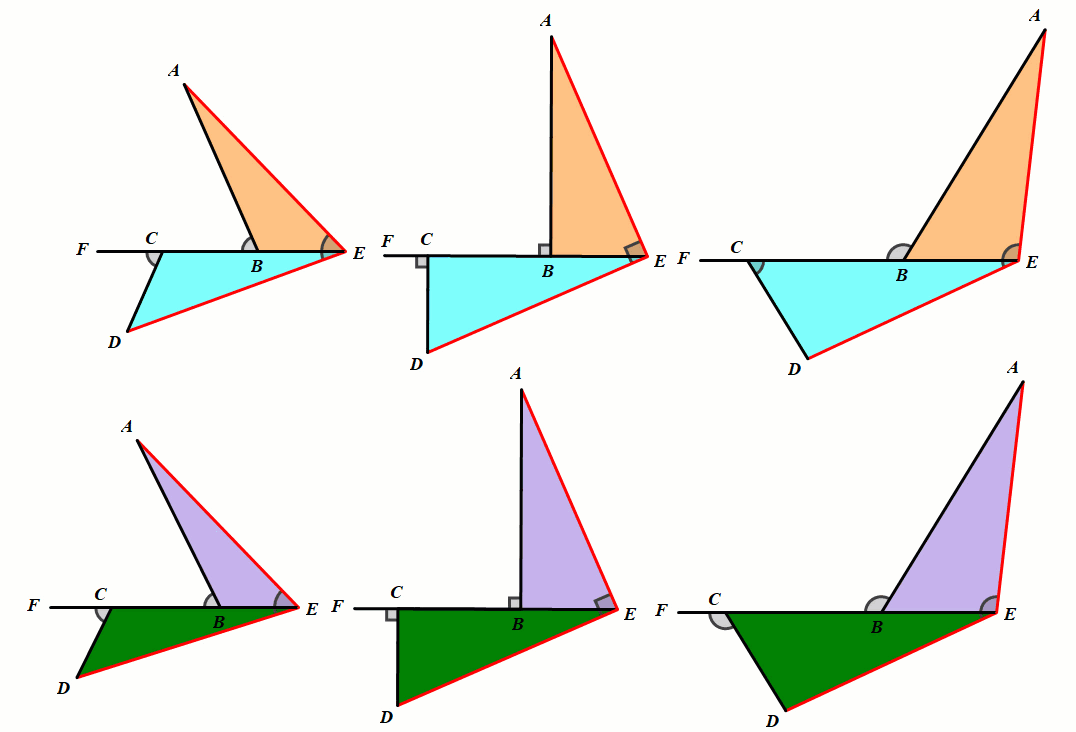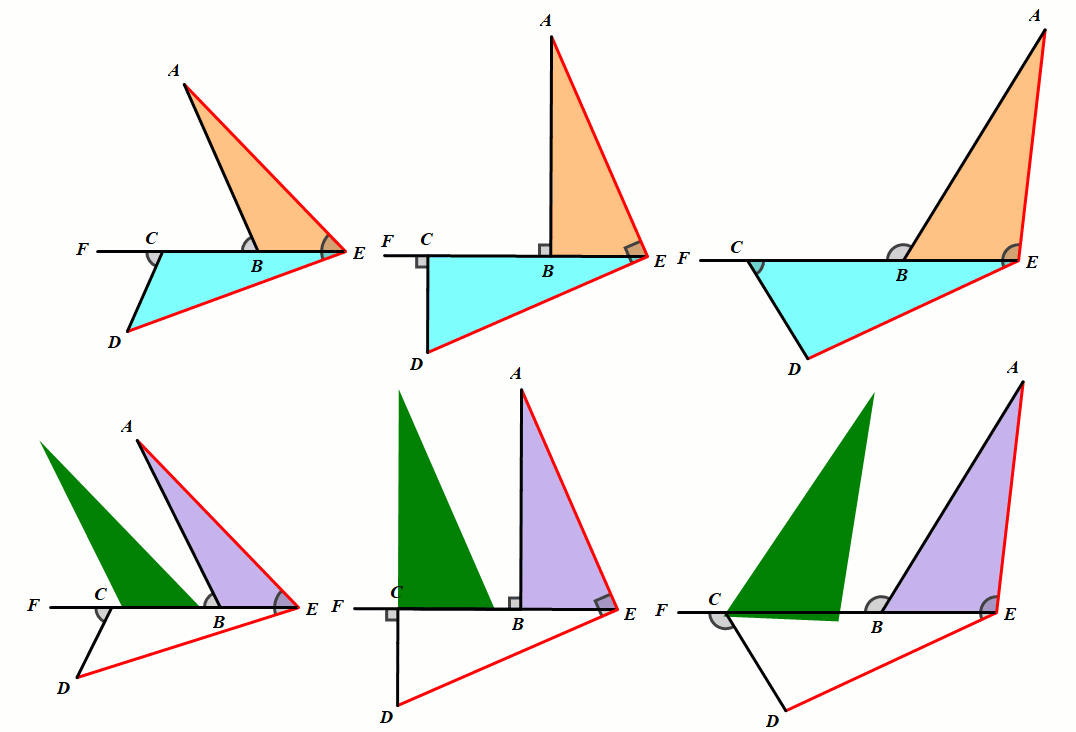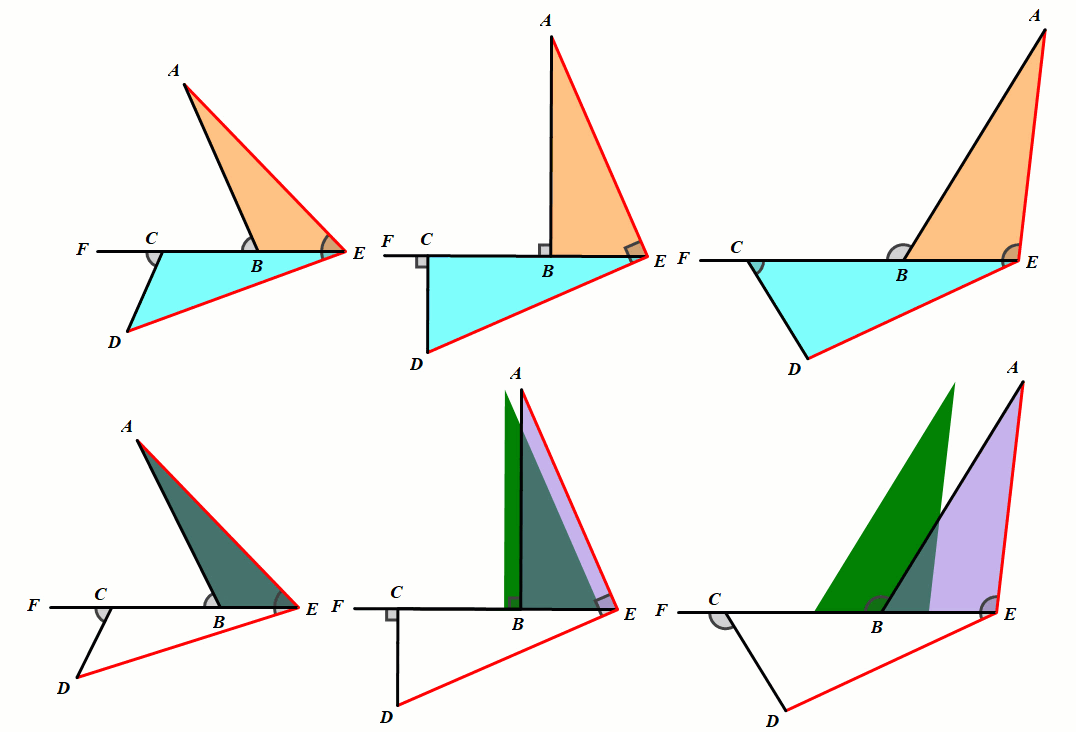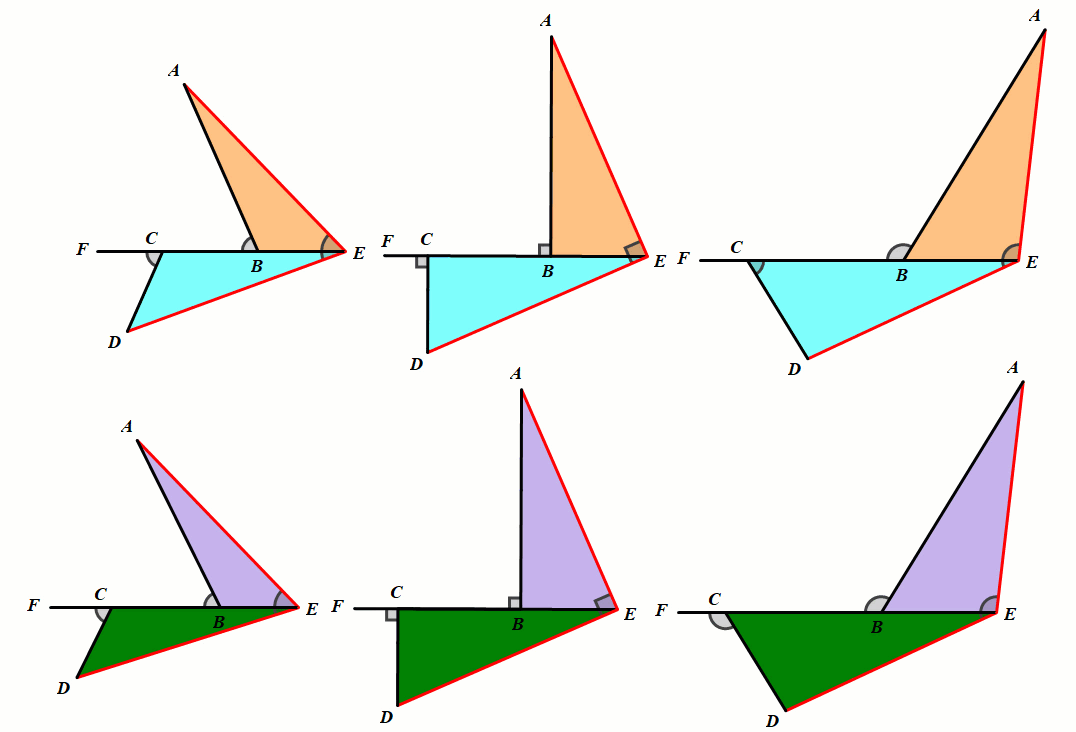
已知：∠AED=∠ABC=∠DCF,AE=DE.

结论：ΔABE≅ΔECD.

平行 中点全等模型

条件:AB∥CD,O为BC的中点.

结论：△AOB≅△DOC.

将军饮马

链接：初中几何最值问题基本模型：将军饮马

模型1：定直线与两定点（一动两定型）

（一）距离之和最短（化折为直）

1.两侧型：两点分别在直线两侧（基础本质型）

已知：如图①，定点A、B分别位于直线L的两侧.

要求：在直线L上找一点P,使得PA PB的值最小.

作图：连接AB与直线L交于点P,点P即为所求作的点，PA PB的最小值即为线段AB的长度.

证明：在直线L上任取一点动点P'，连接AP'，BP'.

在△ABP'中，

∵AP' BP'≥AB,即AP' BP'≥PA PB，

∴当线段AB与直线L相交于点P时，PA PB最小.

结论：PA PB最小(AB)

---

2.同侧型：两点在直线同侧（将军饮马）

已知：如图①，定点A、B位于直线L的同一侧.

要求：在直线L上找一点P,使得PA PB的值最小.

作图：作点A、B任意一点关于直线L的对称点,

连接AB'交直线L于点P，则点P即为所求.

证明：根据轴对称的性质知直线L为线段BB'的中垂线，

由中垂线的性质得PB=PB',要使PA PB最小，则需PA PB'最小，从而转化为两侧型.

结论：PA PB最小(AB').

---

（二）距离之差的绝对值最大

1.同侧型：

已知：如图①，定点A、B位于直线L的同一侧（A、B两点到L的距离不等）.

要求：在直线L上找一点P,使得|PA-PB|的值最大.

作图：连接AB并延长，与直线L交于点P,点P即为所求.

证明：在L上任取一点P'(异于点P),连接P'A，P'B.由三角形三边关系知|P'A-P'B|<AB，即|P'A-P'B|≤|PA-PB|.

结论：|PA-PB|最大(AB).

---

2.同侧型：

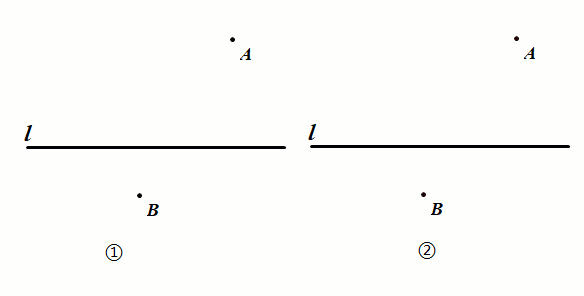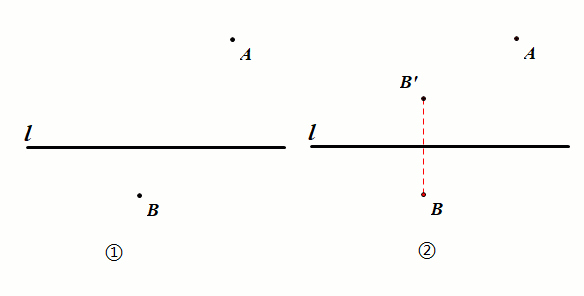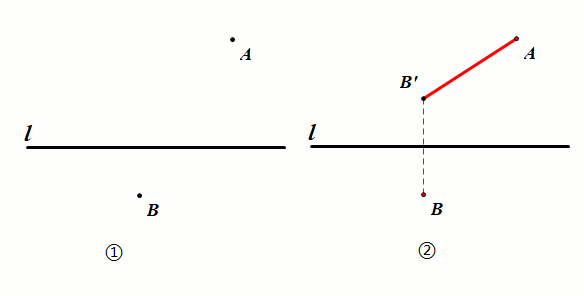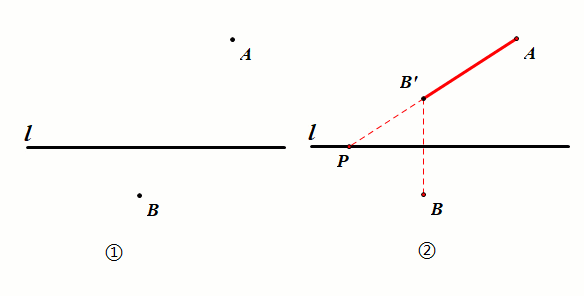
已知：如图①，定点A、B位于直线L的两侧（A、B两点到l的距离不等）.

要求：在直线L上找一点P,使得|PA-PB|的值最大.

作图：作点A、B任意一点关于直线L的对称点,

连接AB'并延长，与直线L交于点P,点P即为所求.

证明：根据轴对称的性质知直线L为线段BB'的中垂线，

由中垂线的性质得PB=PB',要使|PA-PB|最大，则需|PA-PB'|最大，从而转化为同侧型.

结论：|PA-PB|最大为AB'.

---

（三）距离之差的绝对值最小（垂直平分线性质定理应用）

要求：如图①、②，在直线L上找一点P,使得|PA-PB|有最小值.

作图：连接AB,作线段AB的垂直平分线与直线L交于点P，

点P即为所求作的点.

证明：由中垂线的性质得PB=PB,要使|PA-PB|最小为0.

结论：|PA-PB|的最小值为0.

模型2：角与定点（两动一定型）

---

（一）距离之和最短

1.定点在角的外部

已知：如图①，P点为锐角∠MON外一定点.

要求：在射线OM上找一点A，在射线ON上找一点B，使得PA AB的值最小.

作图：如图②，过点P作PB⊥ON于点B,PB与OM相交于点A.此时，AP AB最小.

证明：AP AB≥PB,当且仅当A，P，B三点共线时，AP PQ取得最小值PB,根据点到直线的距离，垂线段最短，当PB⊥ON时，PB最短.

结论：PA AB的最小值为PB.

---

2.定点在角的内部

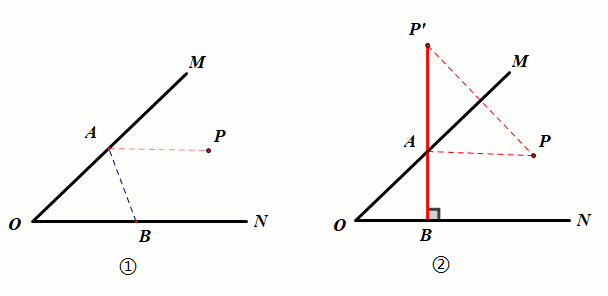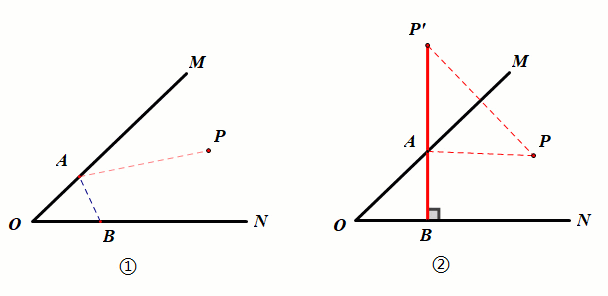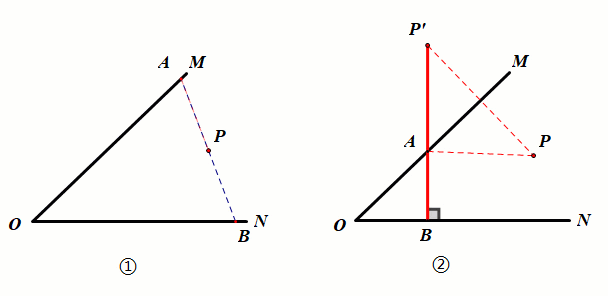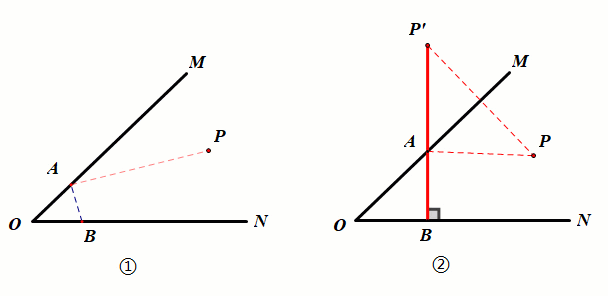
已知：如图①，P点为锐角∠MON内一定点.

要求：在射线OM上找一点A，在射线ON上找一点B，使得PA AB的值最小.

作图：如图②，作点P关于OM的对称点P'，过点P'作ON的垂线分别交OM、ON于A、B.点A、B即为所求作的点.

证明：由轴对称的性质得PA=P'A,要使PA AB最小，只需P'A AB最小，从而转化为定点在角外部模型.

结论：PA AB的最小值为P'B.

---

3.三角形周长最小

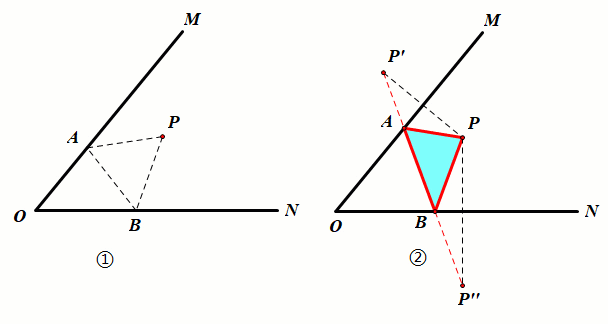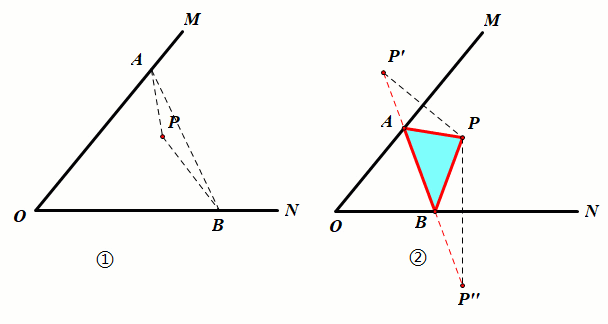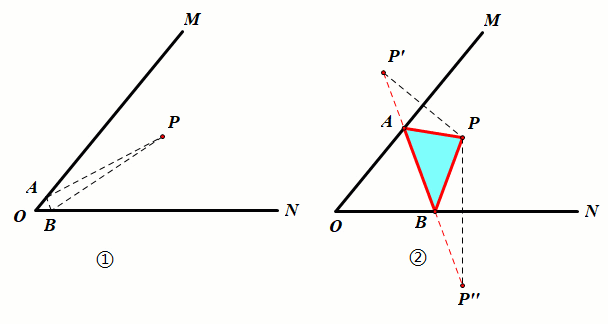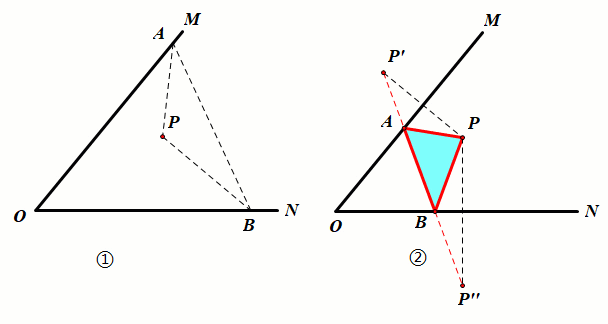
已知：如图①，P点为锐角∠MON内一定点.

要求：在射线OM上找一点A，在射线ON上找一点B，使得△PAB的周长最小.

作图：如图②，分别作P点关于直线OM的对称点P'，关于ON的对称点P''，连接P'P''交OM于点A,交ON于点B,点A、点B即为所求，此时△PAB的周长最小，最小值为线段P'P''的长度.

证明：由轴对称的性质可知AP=AP',BP=BP'',△APB的周长AP AB BP=AP' AB BP'',当P'、A、B、P''四点共线时，其值最小.

结论：△PAB的周长最小为P'P''.

---

4.四边形周长最小

已知：如图①，P、Q为锐角∠MON内的两个定点.

要求：在射线OM上找一点A，在射线ON上找一点B，使得四边形ABPQ的周长最小.

作图：如图②，分别作Q点关于直线OM的对称点Q'，P点关于ON的对称点P''，连接P'Q'交OM于点A,交ON于点B,

点A、点B即为所求，此时四边形ABPQ的周长最小，最小值为线段P'Q' PQ.

结论：四边形ABPQ的周长最小为P'Q' PQ.

---

5.两动两定变式模型

已知：如图①，A、B为两个定点,P、Q为动点.

要求：在射线OM上找一点Q，在射线ON上找一点P，使得AP PQ QB最短最小.

作图：如图②，分别作A点关于直线ON的对称点A'，B点关于OM的对称点B'，连接A'B'交OM于点Q,交ON于点P,点P、点Q即为所求，此时AP PQ QB最小，最小值为线段A'B'.

结论：AP PQ QB最小为线段A'B'的长.

搭桥模型

模型1

已知：如图①，直线m∥n,A,B分别为m上方和n下方的定点（直线AB不与m垂直）.

要求：在m,n之间求作垂线段PQ,使得AP PQ QB的值最小.

解析：PQ为定值，只需要AP QB最小，可通过平移，使P,Q“接头”，转化为基本模型（将军饮马）.

作图：如图②，将点A沿着平行于PQ的方向，向下平移至点A'，使得AA'=PQ,连接A'B交直线n于点Q,过点Q作PQ⊥n于点Q,交直线m于点P,线段PQ即为所求，此时AP PQ QB最小.

证明：由作图过程可知四边形QPAA'为平行四边形，则QA'=PA,当B,Q,A'三点共线时，QA' QB最小，即PA QB最小，又PQ长为定值，所以此时AP PQ QB的值最小.

---

模型2

已知：如图①，定点A,B分布于直线m两侧，长度为a（定值）的线段PQ在m上移动（P在Q左边）.

要求：确定PQ的位置，使得AP PQ QB的值最小.

解析：PQ为定值，只需要AP QB最小，可通过平移，使P,Q“接头”，转化为基本模型（将军饮马）.

作图：如图②，将点A沿着平行于m的方向，向右移至点A'，使AA'=PQ=a,连接A'B交直线m于点Q,在m上截取PQ=a(P在Q左边)，则线段PQ即为所求，此时AP PQ QB的最小值为A'B PQ，即A'B a.

证明：由作图过程可知四边形APQA'为平行四边形，则QA'=PA,当B,Q,A'三点共线时，QA' QB最小，即PA QB最小，又PQ长为定值，所以此时AP PQ QB的值最小.

---

模型3

已知：如图①，定点A,B分布于直线m的同侧，长度为a（定值）的线段PQ在m上移动（P在Q左边）.

要求：确定PQ的位置，使得四边形APQB的周长最小.

解析：AB长度已经确定为定值，只需要AP PQ QB最小，可通过作A点关于m的对称点，转化为基本模型（将军饮马）.

作图：如图②，作A点关于m的对称点A'，将点A'沿着平行于m的方向，向右移至点A''，使A'A''=PQ=a,连接A''B交直线m于点Q,在m上截取PQ=a(P在Q左边)，则线段PQ即为所求，此时四边形APQB的周长最小为A''B AB PQ，即A''B AB a.

中点模型

模型1 倍长中线或类中线构造全等三角形

条件：AD是中线，延长AD至点E使DE=AD.

结论：△ADC≅△EDB(SAS)

---

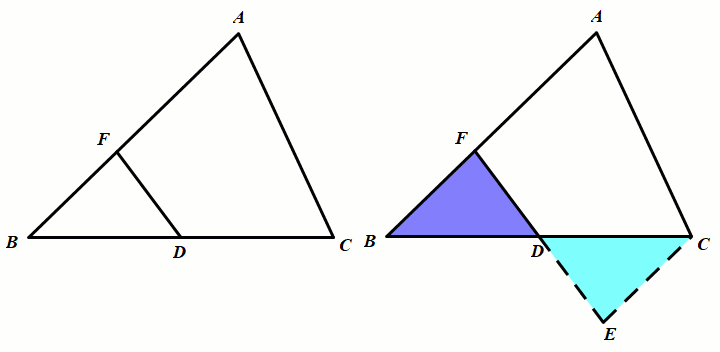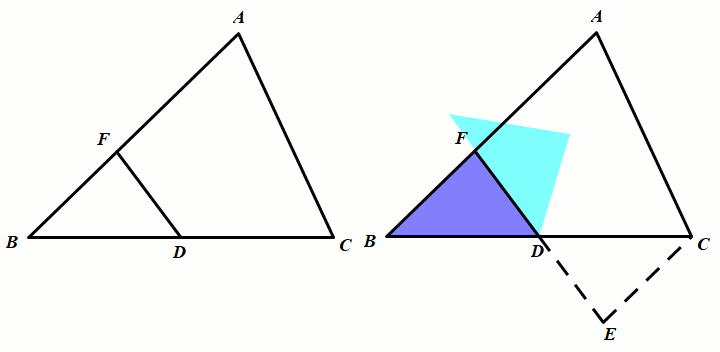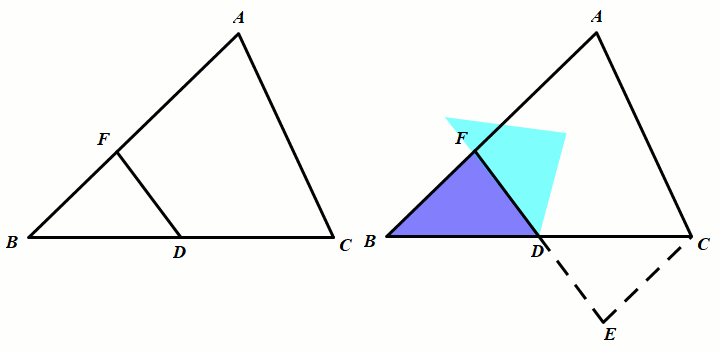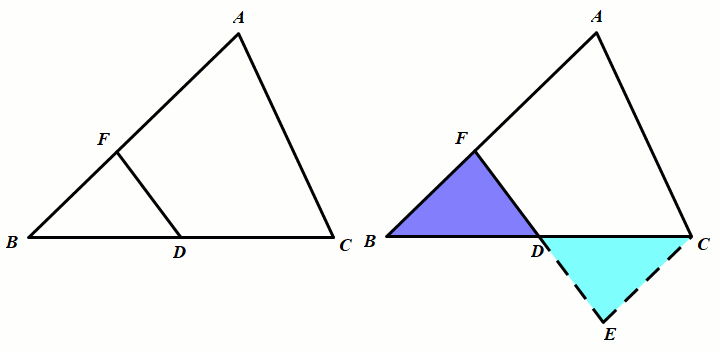
条件：D是BC的中点，延长FD至点E使DE=AD.

结论：△FDB≅△EDC(SAS)

模型2 三线合一模型

等腰三角形中有底边中点时，常作底边的中线，利用等腰三角形，，三线合一”的性质得到角相等或边相等，为解题创造更多的条件，当看见等腰三角形的时候，就应想到.“边等、角等、三线合一”.

模型3 中位线模型

在三角形中，如果有中点，可构造三角形的中位线，

利用三角形中位线的性质定理：DE//BC,且DE= BC来解题.中位线定理中既有线段之间的位置关系又有数量关系,该模型可以解决角相等，线段之间的倍半、相等及平行问题.

模型4 斜边中线模型

在直角三角形中，当遇见斜边中点时，经常会作斜边上的中线，利用直角三角形斜边上中线等于斜边的-半，即CD= AB，来证明线段间的数量关系，而且可以得到两个等腰三角形:△ACD和△BCD,该模型经常会与中位线定理一起综合应用.

半角模型

模型1 基本模型

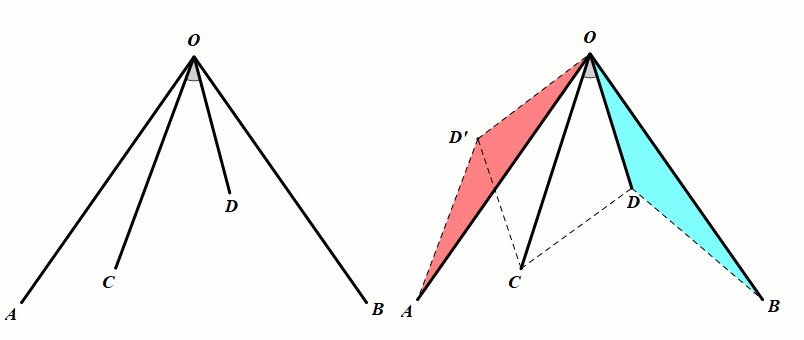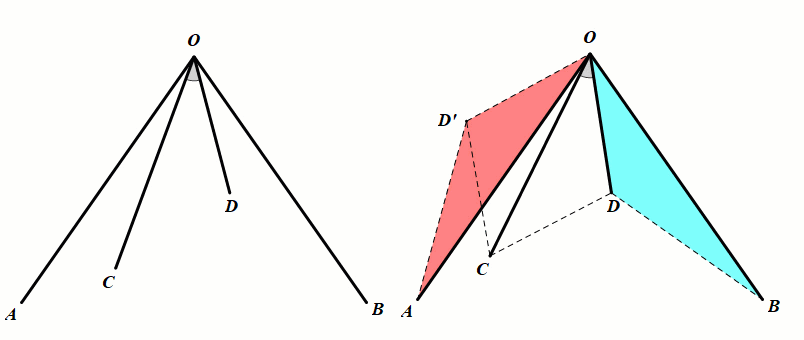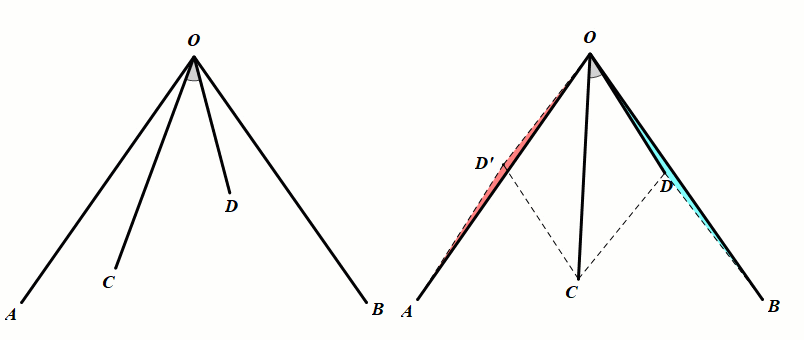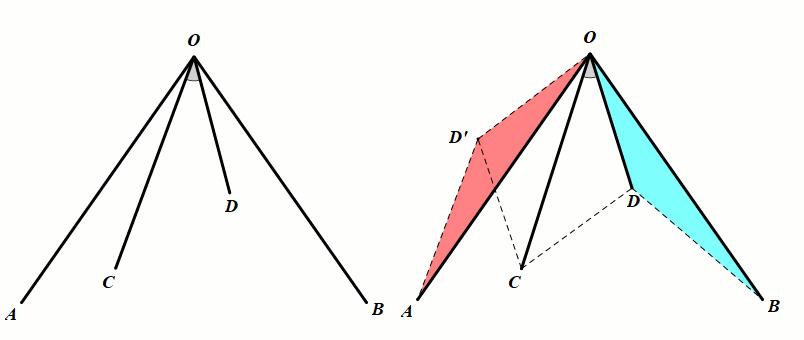
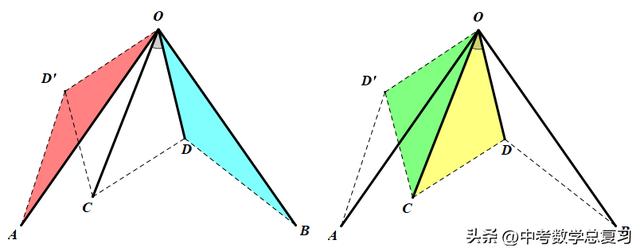
条件：OA=OB,∠AOB=2∠COD.

结论：△ODB≅△OD'A（旋转全等）；△OCD≅△OCD'（对称全等）.

模型2 四边形半角模型

条件：∠B ∠D=180°,AB=AD,∠BAD=2∠EAF.

结论：如图①△ADF≅△ABG；如图②△ABE≅△ADH（旋转全等）；

△AEF≅△AEG≅△AHF（对称全等）.

模型3 正方形半角模型

条件：在正方形ABCD中，∠EAF=45°.

结论：

（1）EF=BE DF；（旋转全等、对称全等）

（2）Rt△ECF的周长=2AB；

（3）△ABE的面积 △ADF的面积=△AEF的面积；

（4）AQ=AB；

---

条件：在正方形ABCD中，∠EAF=45°.

结论：

（5）△AOM∼△ADF,△AON∼△ABE；（相似比1:根号2）

（6）△AMN的面积 四边形MNFE的面积=△AEF面积的一半；

---

条件：在正方形ABCD中，∠EAF=45°.

结论：（7）△ANE,△AMF为等腰直角三角形.

---

条件：在正方形ABCD中，∠EAF=45°.

结论：（8）A、D、F、E四点共圆，A、B、E、N四点共圆，M、N、F、C、E五点共圆.

---

条件：在正方形ABCD中，∠EAF=45°.

结论：（9）△ANM∼△DNF∼△BEM∼△AEF∼△DAM∼△BNA.

模型4 等腰直角三角形半角模型

条件：Rt△ABC中，AC=BC,∠ECF=45°.

结论：△BCF≅△ACP(旋转全等),△PCE≅△FCE（对称全等），

.

---

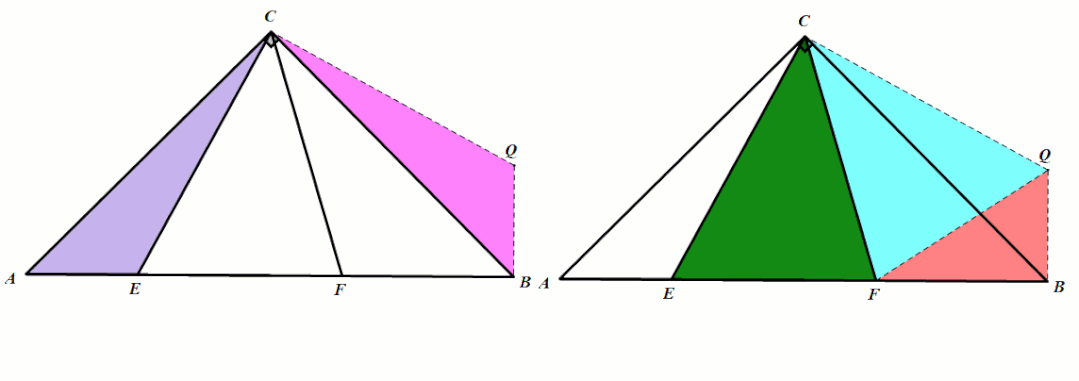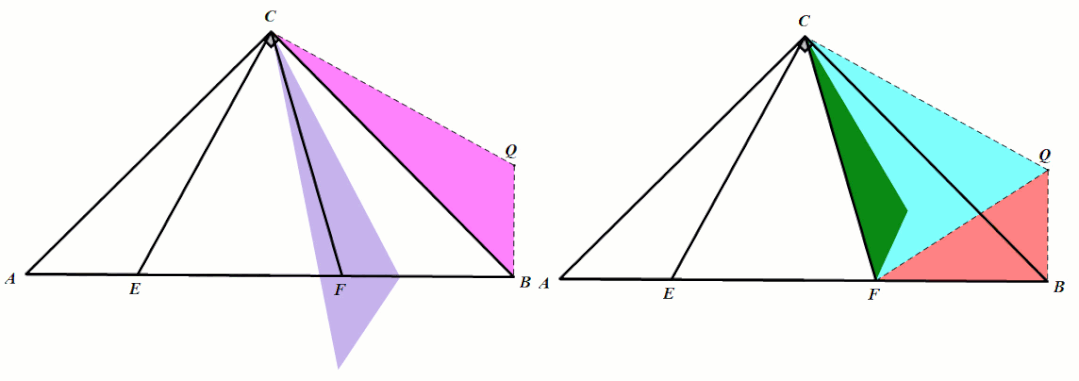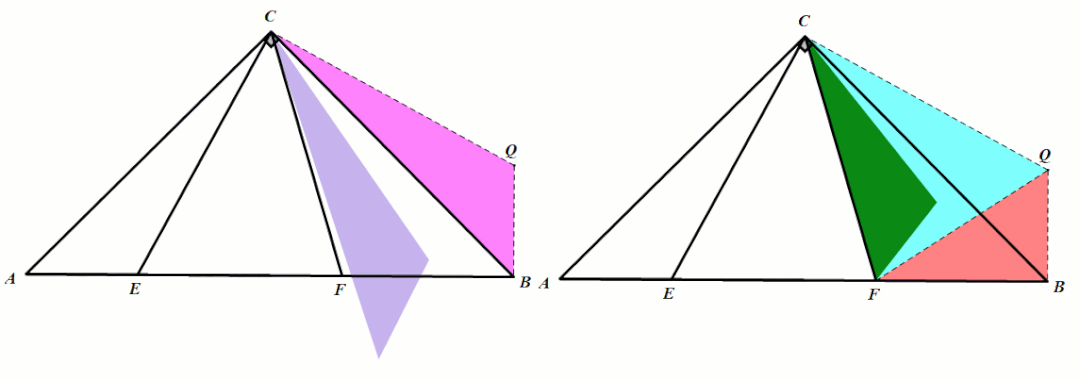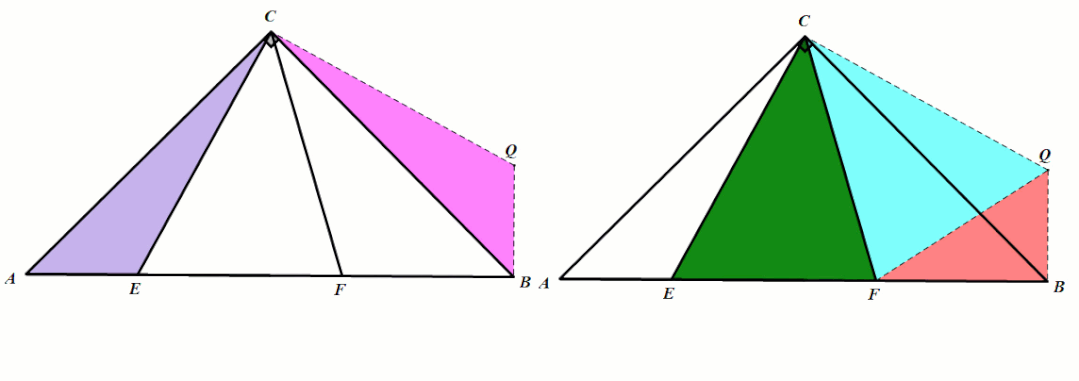
条件：Rt△ABC中，AC=BC,∠ECF=45°.

结论：△ACE≅△BCQ(旋转全等),△ECF≅△QCF（对称全等），

.

相似模型

模型1 链接：A字型相似

链接：平行A字型相似

条件：DE∥BC

结论：△AED∼△ABC.

---

非平行A字型相似

条件：∠AED=∠ACB

结论：△AED∼△ACB

模型2 链接：8字型相似

平行8字型相似

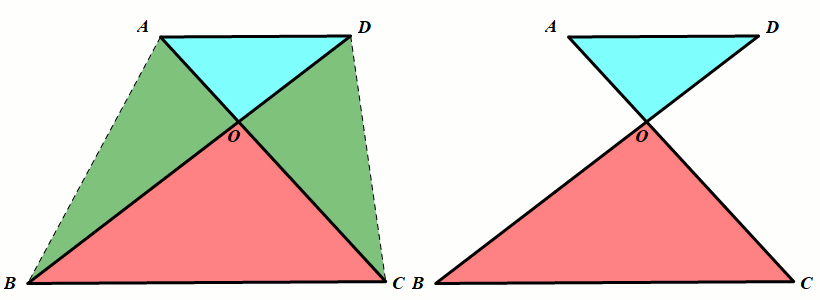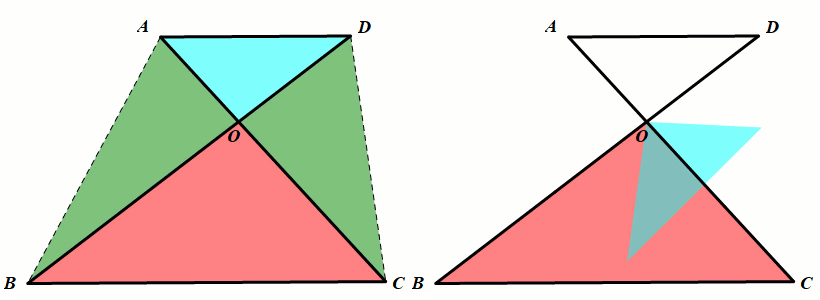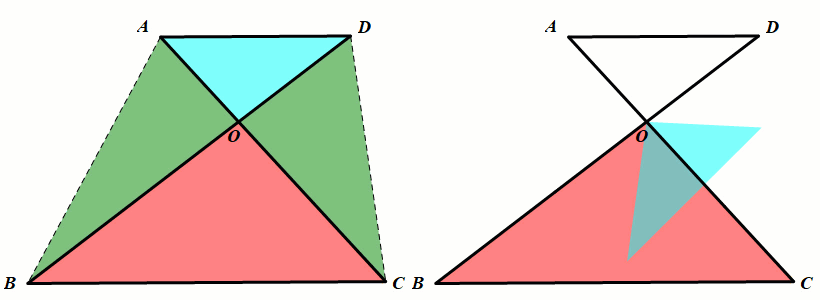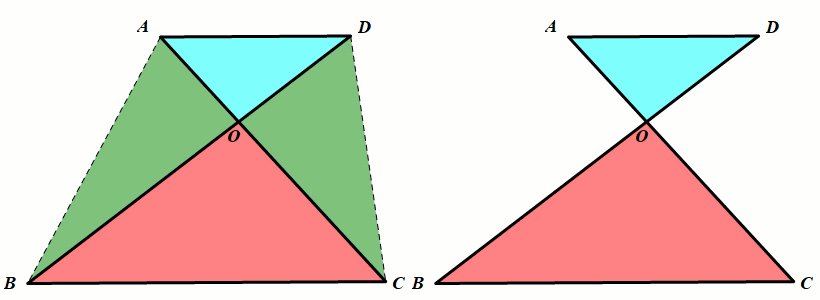
条件：AD∥BC

结论：△AOD∼△COB(上下相似)，左右不一定相似，

(面积相等).

---

非平行8字型相似

条件：∠DAC=∠CBD

结论：A、B、C、 D四点共圆

△AOD∼△BOC(上下相似)

△AOB∼△DOC(左右相似)

模型3 ⇒共边共角型相似

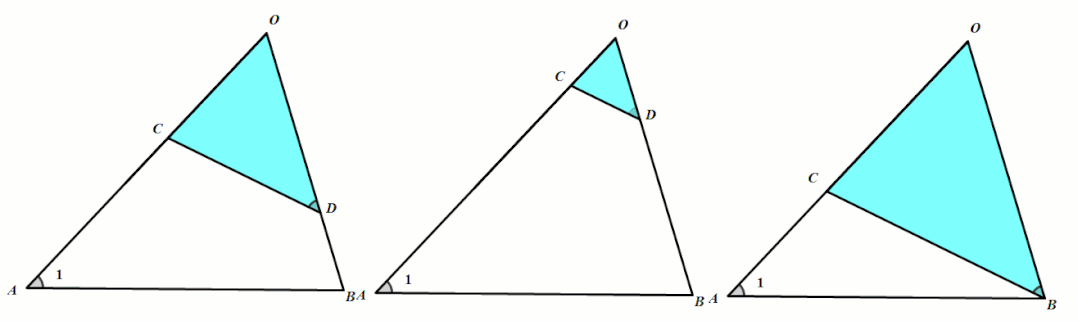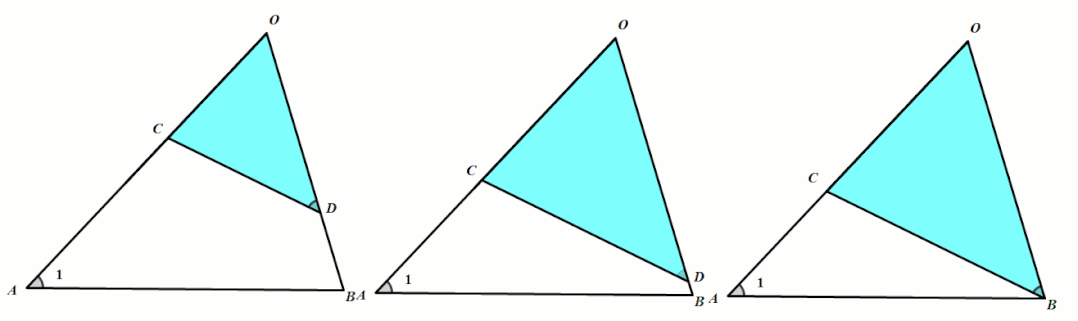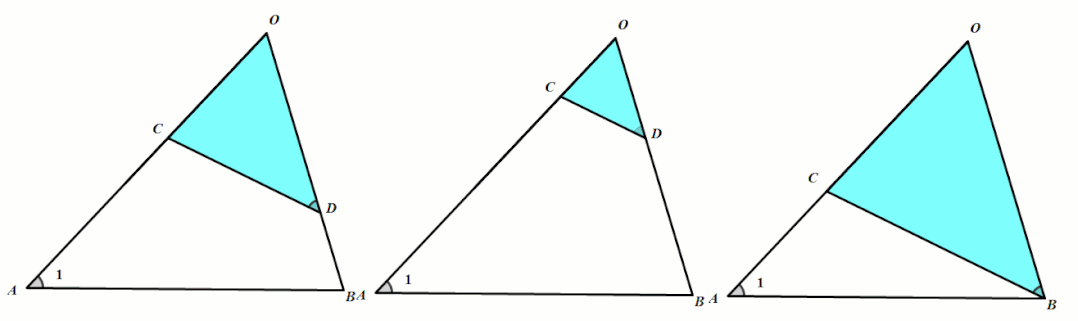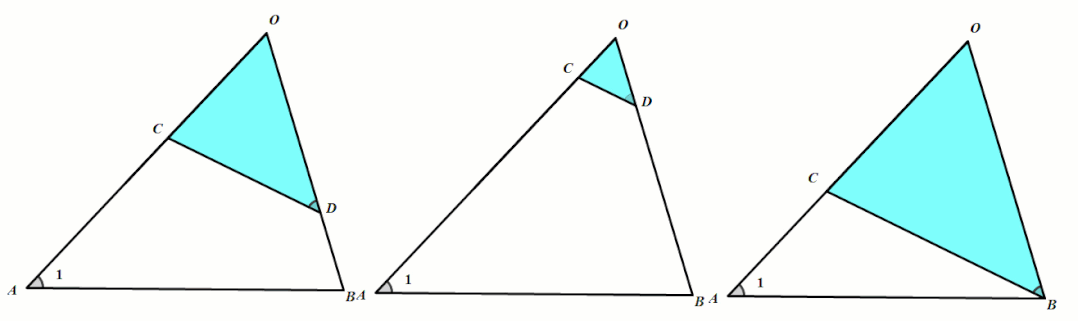
共边共角型是“不平行A字型”（链接：手拉手旋转型相似）的特殊情况.当D点运动到B点时即为“共边共角型”.

条件：∠OAB=∠OBC.

结论：△OBC∼△OAB.（OB是OC和OA的比例中项）

模型4 手拉手旋转型相似

条件：图①中只需CD∥AB.

结论：ΔOAC∼ΔOBD;∠AEB=∠AOB.

模型5 一线三等角

同侧型

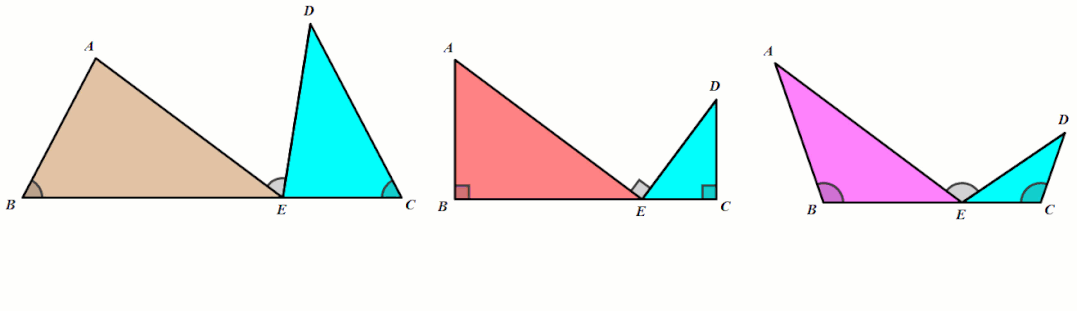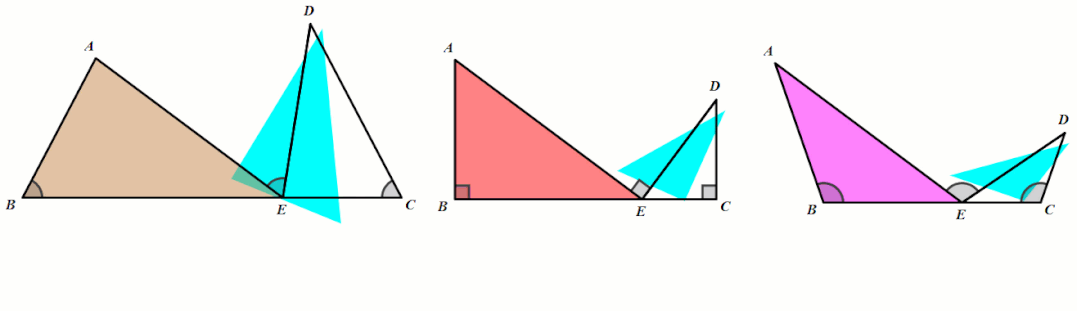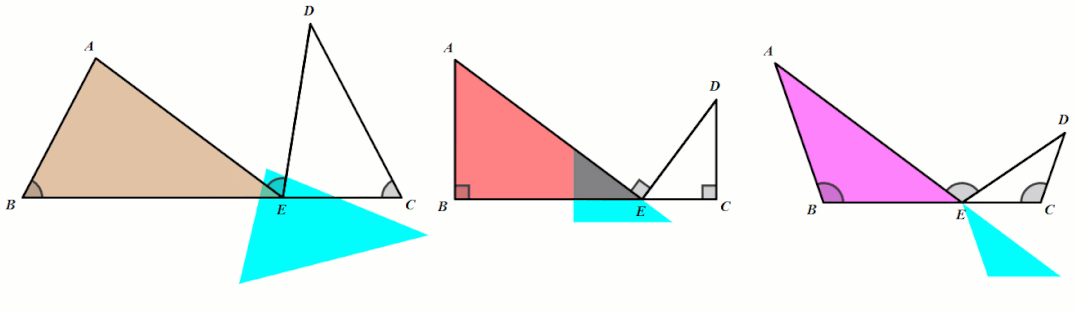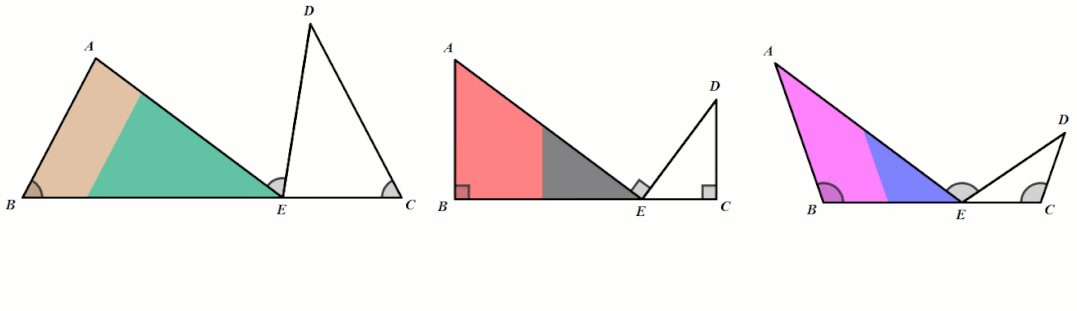
条件：∠B=∠C=∠AED.

结论：△ABE∼△ECD.

---

异侧型

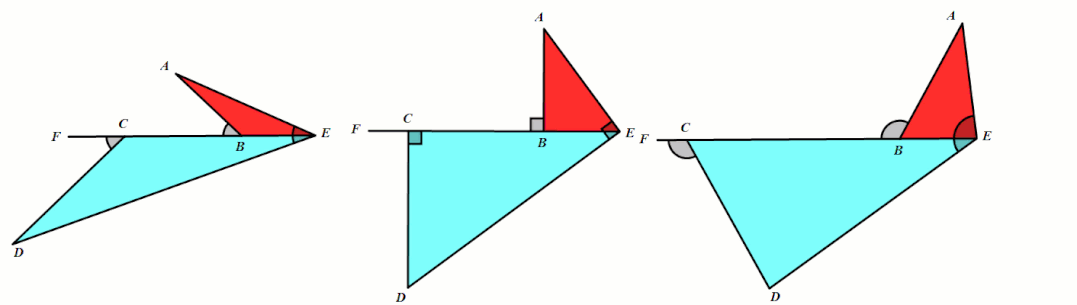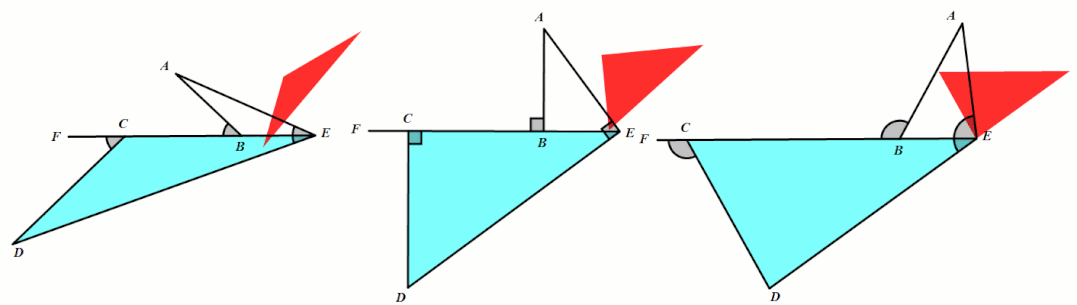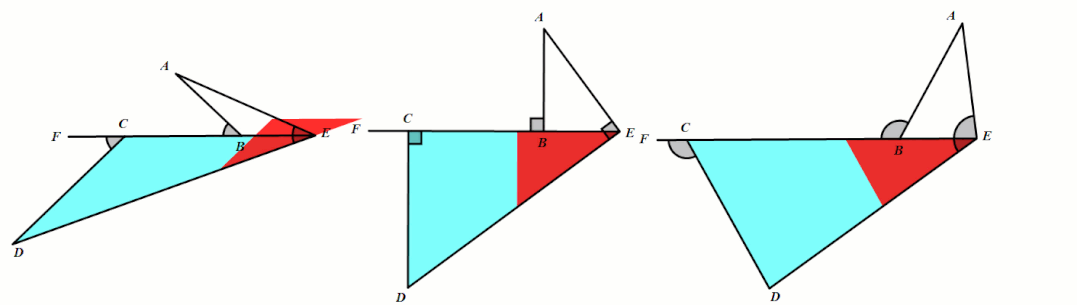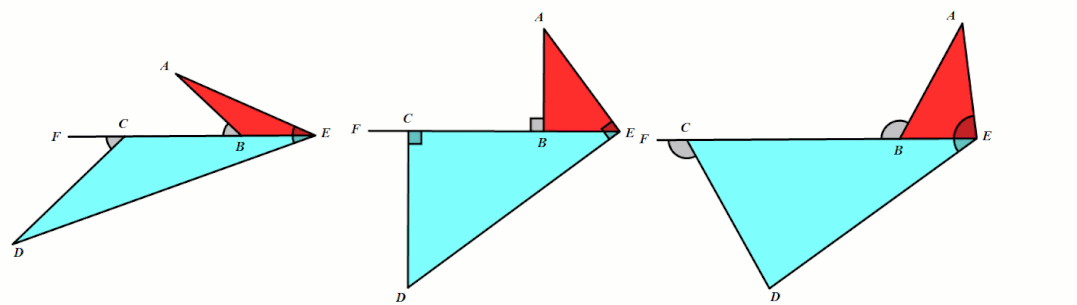
条件：∠AED=∠ABF=∠DCF.

结论：△ABE∼△ECD.

---

一线三等角 中点型

条件：∠B=∠C=∠AED,E为BC的中点.

结论：△ABE∼△ECD∼△AED;

AE平分∠BAD、DE平分∠ADC.

模型6 圆中的相似

圆中的8字型（相交弦定理）

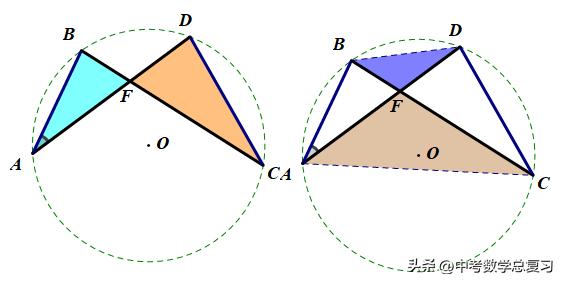
结论：

△AFB∼△CFD(左右相似)；

△BDF∼△ADC(上下相似)；

AF·FD=BF·CF；

圆中8字型相似

---

切割线定理

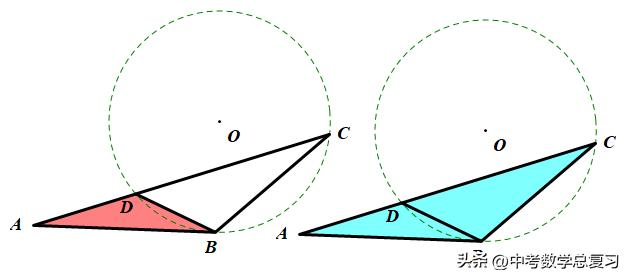
条件：AB为切线，AC为割线.

结论：△ABD∼△ACB(共边共角型相似)，

(AB为比例中项).

---

双割线定理

条件：AC、AF为割线.

结论： .

---

,