自制音调可变的乐器（对一种自制乐器进行音高修正和音色分析）

作者：郑智 吴炳炎 王伟帆

01概述

---

在本学期的另一门课程《机械制造基础》中，我们利用3D 打印技术，设计并制造了一种类似单簧管的木管乐器。在这篇小论文中，我们将利用信号与系统课程所学的知识，对该乐器的音色和音高进行分析和修正。文章的主要内容如下：

首先，经过测试，我们发现我们自制的乐器存在一定的音准问题。因此，在第2节中，我们将基于吹奏单音时的录音，通过DFT、频谱变换和IDFT，恢复出具有正确音准的时域波形。基于正确的单音时域波形，我们进一步对由该乐器吹奏的一首乐曲的音频进行了音高修正。在这个过程中，我们发现，频谱伸缩变换能够有效将乐器的音域从离散音高延拓到连续音域，并基于此将部分乐器的音高延拓到其音域之外，从而能够制作部分乐器因为超出音域而无法吹奏的乐曲。

在主观感受上，我们自制的乐器的音色比较接近单簧管。同时，我们希望能够设计一种方法客观地评价该乐器的音色，并将其和其他木管乐器音色进行比对。在第3节中，我们训练了1 个能够提取乐器单音频谱特征，并区分4 中木管乐器音色的多层感知机(MLP)，使其为我们自制的乐器的频谱计算频谱特征。实验结果表明，模型计算的频谱特征同样接近单簧管的频谱特征，与我们的主观判断一致。

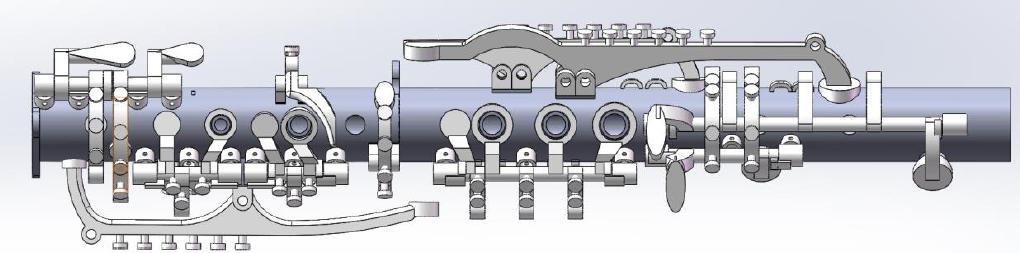
▲ 乐器设计图

▲ 乐器制作实物

02频谱分析处理

---

1.频谱的提取与简化

（1）乐器单音频谱

在理想情况下，单音的频谱可以写成如下形式:

其中，是基频，也就是人耳感知乐器的声音频率。是第k节的泛音的频率；是对应泛音的幅值，并满足；而是第k阶泛音的相角。

由于人的耳朵对于相位不敏感，可以认为人耳只能够感知。由于频谱包含了时域波形的全部信息，因此也必然包含了单音的听觉三要素：音高、音色和响度。可以简单的认为，决定了音高，频谱能量对应响度，而频谱的形状对应音色。对于单音频谱，频谱的相撞可以有归一化的泛音峰值序列完全描述。

在实际情况中，各界的泛音并非理想的函数，而是有一定高度和脉宽的尖峰，如下图所示：

![▲ 长堤#pic_center)

这种情况下，可以通过以下共识来计算：

其中是第k阶泛音的频谱范围，是第k阶泛音波峰包含的频谱点。

（2）时域截取

我们将5 种管乐器（单簧管、双簧管、英国管、巴松、长笛）及自制乐器的各个单音进行了FFT。因为每个单音的时域波形在两端有渐强和减弱，我们希望排除这部分影响，所以对每个单音截取中间的较平整的片段。片段大于1 ，故频谱分辨率高于1Hz；采样率 = 48000，故最大频率为24000 。截取片段前后对比如下（示例为单簧管E）:

可见截取后各个峰高度比例大致不变，虽然各个峰变宽，但是类似于噪音的震荡减少了，细微的小尖峰抹去了。

（3）频谱简化

于是我们得到了5*10 14个单音的频谱。但是，尽管每个单音的频谱仅有约10～25个峰，却需要数万个点来表达，十分不经济，也不方便进一步的处理。所以我们希望对频谱进行简化，只记录各个主要峰的频率和幅值。

我们选择只记录峰值大于最高峰1%的峰；如果两个峰过于接近，距离小于基频的1/10，则将两个峰合并。我们分别记录了各个峰的峰值和面积，两者结果略有不同，虽然我们认为面积代表各频率的能量，更为合理，但后续实验表明两者对音色的影响有限，难以分清孰优孰劣。最后将幅值归一化，使每个频谱的各峰幅值平方和为一定值。两种方法得到的简化频谱如下所示（示例为单簧管E）：

▲ 单簧管E音频谱

2.音符的时域生成

（1）任意时长单音的生成

我们虽然截取了各单音的音频片段，但是其长度固定，若要得到时长更长的单音，如果简单地将其复制拼接，在拼接处会有明显的不连续感，音质很差。对于音频片段FFT得到的频谱，如果逆变换IFFT，得到的仍然是原长的音频；如果对频谱修改再IFFT，则往往结果为复数。

得益于简化频谱，我们可以直接傅立叶级数求和。我们已拥有各主要频率的频率值和幅值，虽然缺少相位，但人耳对相位不敏感，且各频率之比不是严格的倍数关系，相位的影响不大；且后续实验了各频率设置随机相位，得到的音频无差别。

于是，我们生成得到了各单音的任意时长音频。与原音频相比，生成的单音音色有一定改变，但仍可分辨。主要差别在，原频谱在低频部分除了峰外也有一定的值，而简化时忽略，低频份量减小；生成的音频缺少管乐器气息的变化，一成不变，较为机械；原音频为实际录音，有一定沙哑感，而生成的更为致密。（我们在附件中附上了几个样本，老师可以亲自感受一下哈）

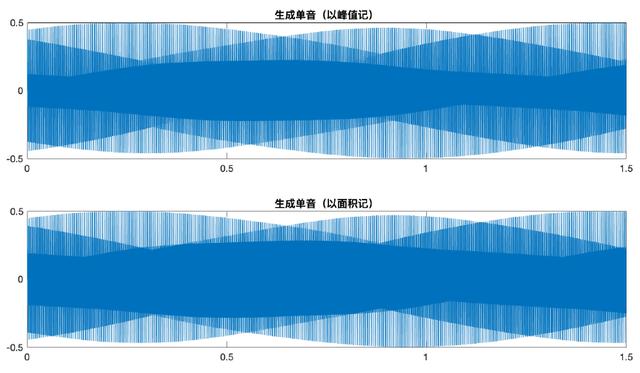
（2）任意频率单音的生成

有了各音符的频谱，我们就可通过修改频谱，来任意改变音符的频率。一方面，由于自制乐器的频率略有不准确，可以将其修正到准确的频率（在附件中附上了修正前后对比）。另一方面，我们可以将制作出本不属于某种乐器音域的音符，将某种乐器的音域大大拓展。

我们起初设想的是，同一乐器不同音符的频谱是极为相似的，可以通过插值得到某两个已有频率之间的频率。后来频谱分析后发现，即便是同一乐器，不同音符的频谱也差别很大（如下图所示），这样的话插值就意义不大了，所以选择直接将某一音符的频谱伸缩变换，得到另一频率的音符。

3.乐曲生成

我们已经得到了，或者说可以得到5 1种乐器的各个音符，于是想进一步由音符生成乐曲。我们将乐曲的音符依次记录在txt文件，包含其音高和时长，依此生成乐曲。由频谱逐个音符生成，原本不包含的音符从其他音符频谱转换。

我们用5 1种乐器分别生成了一曲《欢乐颂》，其中一个低音G是超过部分上述乐器的音域的，我们从C生成了这个音符，拓展了乐器的音域，完成了整个欢乐颂。为了保证音符之间连接处连续，将每个音符与半个周期的sin函数相乘。生成的欢乐颂如下图（示例为长笛），乐曲也置于附件中。

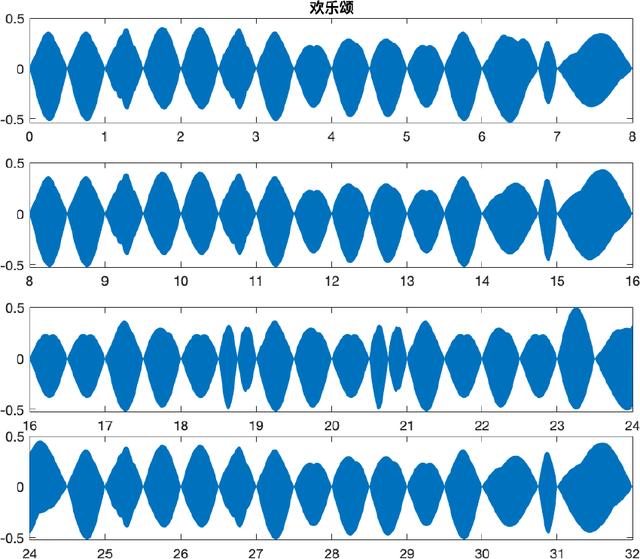
▲ 欢乐颂乐曲波形

此外，我们还生成《新年好》《小星星》等乐曲。其中，生成的《浮夸》片段横跨低音A 到高音A，原本用单一管乐器是难以演奏的，我们也用这种方式成功生成。

4.乐曲音高修正

基于2.3 中所述的方法，我们对自制乐器的单音音频进行处理，得到具有准确音高的单音波形，并基于此对一首由该乐器吹奏的乐曲进行了修正。详见补充材料。

03频谱特征提取和分析

---

根据主观的听觉感受，我们自制的乐器音色接近于单簧管音色。这符合我们的预期，因为该乐器的按键系统、音孔排布、发声装置都在很大程度上借鉴了单簧管的设计。为了更加客观地评价我们自制的乐器的音色，我们试图使用一种相对客观的方法来对比自制木管乐器和其他木管乐器的音色。

当前主流音色理论认为，频谱能量分布是决定乐器音色的重要因素[1]。一个最直接的办法是观察和比对不同乐器声音的频谱特征。在1 中，我们已经计算了长笛、单簧管、双簧管、英国管、巴松，以及我们自制的乐器在等5 种乐器在f-g1 范围内的8~10 个单音的频谱，并用归一化的泛音波峰面积序列来描述频谱形状。因此，我们尝试直接对频谱进行观察，并总结出能够区分出不同音色乐器的特征和标准。

然而，我们发现，凭人眼观察实际上很难看出能够区分不同乐器音色的频谱特征，且即使是同一乐器，其不同音高的单音的频谱形状也可能存在较大差异。因此，我们尝试使用一个多层感知机MLP 来提取频谱特征，并训练其区分4 种常见木管乐器(长笛、单簧管、双簧管、巴松)的音色，最后，用训练好的MLP 为我们自制的乐器提取频谱特征，计算自制乐器的频谱特征和其他乐器的特征的相似或接近程度，作为对 自制乐器音色的一种客观评价。

▲ 多层感知机(MLP)的结构示意图

MLP 以频谱前k 阶泛音波峰面积为输入(k 的取值在10~20 左右，在后续的试验中，k=10)，得到30 维频谱特征向量。激活函数为ReLU()。损失函数定义如下:

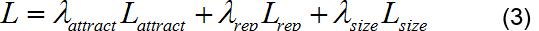
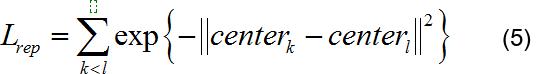
其中，表示该批量中属于第k 类乐器的全部特征向量的质心。训练样本为4 种乐器，各10 个单音的归一化泛音波峰面积序列，采用全局梯度下降算法训练200，轮。用PCA 和t-SNE 算法对训练好的MLP 提取的4 种木管乐器的频谱特征进行可视化，结果如下:

▲ 四种木管乐器的频谱特征PCA降维可视化结果

▲ 四种木管乐器的频谱特征t-SNE可视化结果

可见，模型基本上能够区分4种不同乐器的音色。在PCA分析中，bassoon和flute重叠较多，但在t-SNE算法中这2种区域重叠部分较少，可能与PCA的流形学习能力不如t-SNE有关。通过在同一乐器2个相邻单音之间插值得到的频谱，或许能够用于数据增强来提升性能，但考虑该模型已经基本满足要求，我们不再试图优化模型性能。

然后，我们尝试让这个训练好的MLP，提取自制乐器的频谱特征，可视化结果如下:

▲ MLP提取四种木管乐器的频谱特征PCA降维可视化结果

▲ MLP提取四种木管乐器的频谱特征t-SNE降维可视化结果

可见，模型计算的自制乐器的频谱特征，和单簧管频谱特征有较大重叠，模型认为我们自制的乐器和单簧管音色最为接近，与我们的主观判断一致。

※ 参考文献

[1]Emily J. Allen, et al. Encoding of Natural Timbre Dimensions in Human Auditory Cortex. Neuroimage, 2018 February 01; 166: 60-70.

,