点是原点（点与空间）

话题：#科学# #数学# #点集拓扑#

小石头/编

---

点是人们对于位置的抽象，由点组成的集合称为点集，具有一定性质的点集称为空间。

点并不一定是三维空间中的点，例如：和尚脖子上的佛珠、几何作业本上的墨滴、夜幕中那闪闪发光的群星、饭碗里的米粒、视线的焦点、...，也可以是时间上的点，例如：钟表的滴答、情人的心跳、...，还可以是思维里的点，例如：出个点子、痛点、笑点、爱的浪花、小提琴的音符、...，点甚至可以不是点状，例如：墙上的砖头、书页、光线、旋律、回忆、...，因此空间就更是 五花八门了，例如：星空、爱的海洋、扭曲的四维时空、肖邦的月光、一杯牛奶、一块面包、一场梦、... 。

最初的点集 X，除了能确定，任意一个点 x 属于X，记为 x ∈ X，或 不属于 X，记为 x ∉ X，外，其它啥样啥也做不了。可是点毕竟是位置的抽象！人类之所以能 区分三维空间中的位置，就是因为 可以估算不同位置之间的距离，因此 若要让点扮演好代表位置的角色，就必须在点集上加入定距能力，我们称具有 定距 能力的 点集 为 度量空间。

那么如何让点集 定距 呢？

我们先来分析一下 距离的性质。通过生活实践以及《物理学》训练，我们其实已经在直觉上接受了距离这个概念。提到距离，大家就会想到它有如下这些特性：

• 距离是一个 实数；
• 距离没有方向，不能为负数；
• 从 x 到 y 的距离 等于 从 y 到 x 的距离；

对于点 X 中的 任意两点 x, y ，我们 用 d(x, y) 表示 它们之间的距离。将全体实数记为 ℝ，上面根据特性1， d(x, y) ∈ ℝ，而 x, y ∈ X，可见 d 是 X 上的 二元函数，记为：

由特性2 知 d(x, y) ≥ 0。当d(x, y)=0 时，x 和 y 就是同一位置，于是 x = y，反之依然。

特性3 就是 d(x, y) = d(y, x)，这说明 距离 具有 对称性。

对于三角形来说，其边长就是顶点之间的距离，现在问：任意两边之和 与 第三边 之间的 大小关系 是什么？

假设， 对于任意三角形，两边之和 小于 第三边，则 对于上图有，

a b < c

e c₁ < a，e c₂ < b

根据 特性1 和 2，我们知道 a，b， c 和 e 都是 正实数，于是按照实数的代数运算规则，有，

e e c = e c₁ e c₂ < a b < c

进而，

e ≤ 2e = e e c - c < c - c = 0

即，

d(y, w) = e < 0

这显然与 特性2 矛盾。

故，假设不成了，只能是：对于任意三角形，两边之和 大于等于 第三边。

有了以上分析，我们可以正式给 点集 定距了：对于任意点集 X，若 其上的二元函数 d: X × X → ℝ , 满足，

• 正定性：d(x, y) ≥ 0 并且 d(x, y) 当且仅当 x = y；
• 对称性： d(x, y) = d(y, x)；
• 三角不等式：d(x, y) d(y, z) ≥ d(x, z)；

则称 d 为 X 上的 距离（函数）。

佛曰：“一花一世界，一叶一菩提”，这说的是：花与叶尽管是真实世界中的一部分，但是它们依然可以自成一界。比对，度量空间 X，考虑 其中的任意非空子集 A（记为 A ⊆ X），首先A是一个点集，其次，X 上定义的 距离 d 对于 A 中的点 同样适用，因此上，A 也是一个 度量空间，叫做 X 的 子空间。就真实世界来说，其中的任何物体，都它的一个子空间。

接下来，我们将进一步研究 度量空间，这就需要 能看清楚 更多细节。在 现实中，人类借助 显微镜 来观察 微观世界， 受此启发，我们 也可以在 度量空间 中造一个 “显微镜” 来观察 每个点周围的 局部空间。

回想中学《生物》课上，我们对显微镜的使用：

• 首先，将镜头焦点对准玻片 X 上的一个点 a，这样在目镜中就能看清楚 焦点 a 周围半径为 ε 内的点；

• 然后，切换不同放大倍率的物镜，随着放大倍率变化，ε的值也跟着变化。目镜中 我们总是可以看到 X 的局部，所以 ε始终大于0，而 放大倍率增加 ε减小，放大倍率减小ε增加，于是 1/ε 就是 放大倍率；
• 最后，还会移动焦点的位置，以看清其它点周围的状况；

于是，在度量空间，可定义 显微镜 为：

称为 a 点的 一个半径为 ε 的 开球。

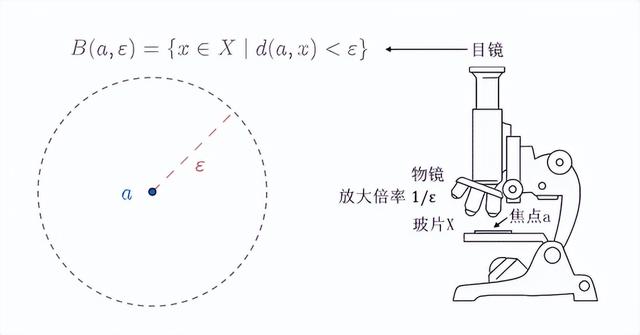
开球 B(a, ε) 就是 显微镜目镜中看到的全部点，其中 a 是焦点，1/ε 是 放大倍率。这样以来，我们就可以通过改变a 和 ε，来在不同 微观等级上 观察 整个 度量空间 了。

一般的点集，属于其的点，是无差别的，可是对于 子空间 则不同。一个苹果，同样是属于苹果的点，有些点我们可以看到，有些不能。可以看到的点是苹果的表皮，而看不见的点是苹果的果肉。

当我们用显微镜去观察苹果时，有，

• 若 焦距 a 对准 果肉，则 通过 不断增加 放大倍率 1/ε ，总会有一个时刻，目镜中全都是苹果；
• 若 焦距 a 对准 果皮，则 无论如何调节 放大倍率 1/ε，目镜中始终一部分是苹果、一部分是苹果之外；
• 若 焦距 a 对准 苹果之外，则 通过 不断增加 放大倍率 1/ε，总会有一个时刻，目镜中将看不到苹果；

若 用 A 表示苹果，X表示整个世界，则 第一种情况就是，

• 对于 a ∈ X ，存在 ε > 0 使得 B(a, ε) ⊆ A，

我们称满足 这个性质的 点 a 为 A 的 内点，A 的全体内点 称为 A 的 内部，记为 A°。

若 将 世界 X 中除去 A 的部分记为 Aᶜ = X \ A（称为 A 的补集），则 令 B = Aᶜ 表示苹果之外，这样 第二种情况可表述为，

• 对于 a ∈ X ，任意 ε > 0 都有 B(a, ε) ∩ A ≠ ∅ 并且 B(a, ε) ∩ Aᶜ ≠ ∅，

称满足 这个性质的 点 a 为 A 的 边界点， A 的全体边界点 称为 A 的 边界，记为 ∂A。聪明的朋友 会发现，A 的边界点，对于 B 也满足 以上性质，所以 也是 B 的边界点，即有，

• ∂A = ∂(Aᶜ)

这符合我们的常识：两个相邻国家的边界是同一个，这还说明：某点集 的边界点 不一定在 该点集内。

将 第三种情况 和 第一种情况对比，大家就会发现，此时的 a 就是 Aᶜ 的 内点，我们称它是 A 的 外点。再对Aᶜ 考虑第一种情况，此时的 a 显然也是 Aᶜ 外点。

将 第一第二种情况混合起来，有，

• 若 焦距 a 对准 果皮，则 无论如何调节 放大倍率 1/ε，目镜中始终可以看到苹果（一部分 或 全部）；

这可表述为，

• 对于 a ∈ X ，任意 ε > 0 都有 B(a, ε) ∩ A ≠ ∅，

称满足 这个性质的 点 a 为 A 的 触点，A 的全体触点 称为 A 的 闭包，记为 A‾ 。我们发现：

• A = A‾ ，称这样的 A 为 闭集；
• B = B°，称这样的 B 为 开集；

显然 闭集 A 的补集 B 是 开集， 开集 B 的 补集 A 是 闭集。

同样是 苹果 的触点，还可以再分类，考虑将 果皮上的 某个点 α 和 苹果分离，虽然 α 还是 苹果的点，但是位置发生改变，这时，

• 若 焦距 a 对准 α，则 通过 不断增加 放大倍率 1/ε ，总会有一个时刻，目镜中将看不到苹果除了 α点之外的点；
• 若 焦距 a 对准 α之外的苹果，目镜中始终可以看到 苹果除a点之外的点（一部分 或 全部）；

后一种情况是，

• 对于 a ∈ X ，任意 ε > 0 都有 (B(a, ε) \ {a}) ∩ A ≠ ∅，

称满足 这个性质的 点 a 为 A 的 聚点，A 的全体聚点 称为 A 的 导集，记为 A' 。边界点类似，某集合的聚点，不一定属于该集合。

从 A 中除去 包含在 A' 中的点，即，A\ A'，就是前一种情况的点，称这些点 为 孤立点。

---

以上就是我们借助显微镜，在 度量空间中 建立的 概念。如果你学过《高等数学》下册的多元微积分，你可能对他们还有印象，如果没有印象也不要紧。这些概念是研究 度量空间 的基础，小石头 将在 续篇中 再进一步详细分析它们。

,