行测的数量关系靠计算还是技巧（行测数量关系是挺难）

在行测备考的过程中，其他题目完成的情况下，还能拿下3道以上的数量关系，那一定是锦上添花。如何在考场上有限的时间内提升数量关系的得分，了解数量的考试题型以及学会挑题就变得至关重要。接下来中公教育就按照数量关系考试题型的频次以及选题的优先级开始学习：

解题思路：

①题干中有明显的的等量关系提示词，直接据此建立等量关系求解。(共多少;是多少;A比B多/少;A是B的几倍;A与B的比例关系等)。

②题干中无明显的等量关系提示词，找不变量建立等量关系求解。

假设空气质量可按良好、轻度污染和重度污染三类划分。一环境监测单位在某段时间对63个城市的空气质量进行了监测，结果表明：空气质量良好城市数是重度污染城市数的3倍还多3个，轻度污染城市数是重度污染城市数的2倍。那么，空气质量良好的城市个数是：

A.33 B.31 C.23 D.27

【答案】A。中公解析：题干中有明显的的等量关系提示词，“空气质量良好城市数是重度污染城市数的3倍还多3个，轻度污染城市数是重度污染城市数的2倍”，可设重度污染城市数为x，则良好、轻度污染城市数分别为3x 3、2x。由题可得x 3x 3 2x=63，解得x=10，所求为3x 3=33，选择A。

特值法一：已知多个完工时间，设工作总量为多个时间的最小公倍数，进而表示出他们的工作效率;

一项工程如果交给甲乙两队共同施工，8天能完成;如果交给甲丙两队共同施工，10天能完成;如果交给甲丁两队共同施工，15天能完成;如果交给乙丙丁三队共同施工，6天就可以完成。如果甲队独立施工，需要多少天完成?

A.16 B.20 C.24 D.28

【答案】C。中公解析：设总工作量为120(8、10、15、6的最小公倍数)，根据题意得合作效率：

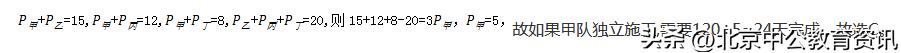
特值法二：已知多个效率之间的比例关系时，直接将效率比看成工作效率;

A工程队的效率是B工程队的2倍，某工程交给两队共同完成需要6天。如果两队的工作效率均提高一倍，且B队中途休息了1天，问要保证工程按原来的时间完成，A队中途最多可以休息几天?

A.4 B.3 C.2 D.1

【答案】A。中公解析：设B工程队的效率为1，A工程队的效率为2，则总工作量为(1 2)×6=18。按原来的时间完成，B工程队完成了1×2×(6-1)=10，则A工程队需要工作(18-10)÷(2×2)=2天，所求为6-2=4天,故选A。

特值法三：已知具体的人或者物的数量时，往往设每个人或者每个物单位时间内的工作量为1。即:直接将人或物的数量，看成工作效率。

某件刺绣产品，需要效率相当的三名绣工8天才能完成。绣品完成50%时，一人有事提前离开，绣品由剩下的两人继续完成;绣品完成75%时，又有一人离开，绣品由最后剩下的那个人做完。请问，完成该件绣品一共用了：

A.10天 B.11天 C.12天 D.13天

【答案】D。中公解析：设每人每天的工作效率为1，则总工作量为1×3×8=24。三人一起工作完成12(即50%)需要24×50%÷3=4天，再由其中两人工作完成6(即75%-50%=25%)需要24×25%÷2=3天，剩下6(即25%)一个人需要24×25%÷1=6天完成。一共用了4 3 6=13天，选择D。

通过学习以上内容，中公教育相信大家对如何挑题有了一定的了解，那如何做对挑选的题目还需要大家不断的练习，小伙伴们加油吧!