解一元二次方程的万能公式(用适当的方法解一元二次方程)
一元二次方程有众多解法,包括利用平方的意义根降次求解、配方法、公式法和因式分解法等。那么当我们面对一个一元二次方程时,到底应该用哪种方法更适合呢?按下来老黄从一元二次方程的一般式开始,给大家做一个全面的分析。
一元二次方程的一般式是:ax^2 bx c=0 (其中a,b,c是常数,且a≠0)。
1、当b=c=0,即一次项系数和常数项都为0时,方程的形式为ax^2=0,这是一元二次方程最简单的形式,方程有两个相等的实数根,x1=x2=0.
2、当b=0,即只有一次项的系数等于0时,方程的形式是ax^2 c=0,此时分成两种情况:
(1)当ac>0时,方程无实数根;
(2)当ac<0时,这时又有两种解法:
解法一是利用平方根的意义,把方程为x^2=-a/c的形式,可以解得方程有两个相反的实数根:x=正负根号(-a/c).
解法二是运用平方差公式进行因式分解,可以得到相同的结果。
例如:x^2-1=0,可以化成x^2=1求解,也可以化成(x-1)(x 1)=0,都可以解得x=正负1.
3、当c=0时,方程是ax^2 bx=0的形式,可以运用提取公式因法因式分解,得到x(ax b)=0,从而解得x=0或x=-b/a.
4、根据判别式△=b2-4ac选择解法:
(1)当△<0时,方程无实数根;
(2)当△=0时,可以运用完全平方公式求解,得到两个相等的实数根x1=x2=-b/2a;
例如:x^2-4x 4=0,判别式△=0(事实上,只要完全平方公式足够熟练,一眼就可以看得出来),因此运用完全平方公式就可以得到(x-2)^2=0,解得x=2.
(3)当△=n^2>0,就可以运用十字相乘法进行因式分解;
例如:2x^2-5x 3=0,△=1=1^2,因此可以运用十字相乘法因式分解得到(2x-3)(x-1)=0,从而解得方程的两个实根x1=1.5, x2=1.
(4)当△>0且△≠n^2,a=1时,建议使用配方法,就是将方程转化成(x-h)^2=-k的形式。其中k=-b/2, k=(4c-b^2)/4.
例如:x^2 2x-5=0可以通过配方,得到(x 1)^2=6. 从而解得x=-1加减根号6.
(5)当△>0且△≠n^2,a≠1时,建议使用公式法。可以直接得到方程的两个根:x=[-b加减根号(b^2-4ac)]/(2a).
例如:4x^2-6x 1=0,利用公式法,可以解得x=(3加减根号5)/4.
注意,只要ac<0,方程就必定有两个不等的实数根。
最后分享一个思维导图,可以直观地看到各种情形下,解一元二次方程的适当方法。
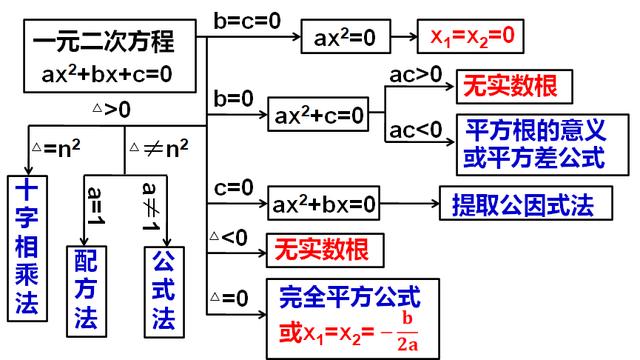
免责声明:本文仅代表文章作者的个人观点,与本站无关。其原创性、真实性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容文字的真实性、完整性和原创性本站不作任何保证或承诺,请读者仅作参考,并自行核实相关内容。文章投诉邮箱:anhduc.ph@yahoo.com






