七年级下整式的运算检测题 整式运算的几何背景与应用

七年级下学期期中考试主要考查平行线与相交线、幂的运算和整式运算，有时会带有部分的二元一次方程组，整式运算中几何背景与应用是期中考试中的常考题型。整式运算中的单项式乘多项式、多项式乘多项式、乘法公式（完全平方公式和平方差公式）以及因式分解等都有几何背景。

例题1：我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式．例如图1可以用来解释a2-b2=（a b）（a-b）．那么通过图2面积的计算，验证了一个恒等式，此等式是

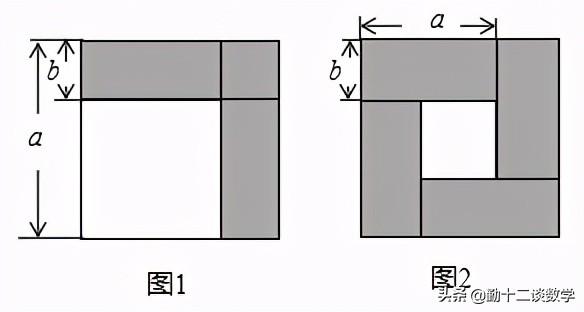
分析：此题根据面积的不同求解方法，可得到不同的表示方法．一种可以是大正方形的面积减去小正方形的面积，还可以表示成4个小长方形的面积。

解：由图②，可知：大正方形的面积为：（a b）^2，小正方形的面积为（a-b）^2，

∴阴影部分的面积为：（a b）^2-（a-b）^2，

部分阴影部分的面积还可表示为：4ab，

∴（a b）^2-（a-b）^2=4ab．

这类题目解题的关键在于对图形的分割与拼合，会用多种方法表示同一图形的面积，然后抓住同一图形的面积相等，得到关系式。

例题2：请认真观察图形，解答下列问题：

（1）根据图①中条件，请用两种不同方法表示两个阴影图形的面积的和；

（2）在（1）的条件下，如图②，两个正方形边长分别为a，b，如果a b=ab=9，求阴影部分的面积．

解：（1）方法一：两个正方形的面积和，即a^2 b^2，

方法二：边长为a b的正方形的面积减去两个空白的长方形的面积，即（a b）^2-2ab，因此有a^2 b^2=（a b）^2-2ab，

（2）图②阴影部分的面积是两个边长分别为a、b的正方形的面积和减去两个直角三角形的面积，即a^2 b^2-1/2a×a-1/2（a b）×b=1/2a^2 1/2b^2-1/2ab=1、2（a^2 b^2-ab）=1/2[（a b）^2-3ab]，当a b=ab=9时，原式=1/2×（81-27）=27，

答：阴影部分的面积为27．

本题考查完全平方公式的几何背景，用不同的方法表示同一个图形的面积是得出关系式的前提。当然，题目一般不会如此简单，会考查完全平方公式的变形，因此也需要掌握完全平方公式的各种变形公式。

因式分解几何背景

例题3：我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．例如由图1可以得到（a 2b）（a b）=a^2 3ab 2b^2．

请解答下列问题：

（1）写出图2中所表示的数学等式；

（2）利用（1）中所得到的结论，解决下面的问题：已知a b c=11，ab bc ac=38，求a^2 b^2 c^2的值；

（3）图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片，请利用所给的纸片拼出一个长方形，使它的面积为2a^2 5ab 2b^2，把拼出的图形画在方框内，并拼出的图形将多项式2a^2 5ab 2b^2分解因式．

分析：（1）根据数据表示出矩形的长与宽，再根据矩形的面积公式写出等式的左边，再表示出每一小部分的矩形的面积，然后根据面积相等即可写出等式．

（2）利用（1）中所得到的结论，将a b c=11，ab bc ac=38作为整式代入即可求出．

（3）找规律，根据公式画出图形，拼成一个长方形，使它满足所给的条件．