奇葩的数学定理（科普浪漫的数学）

有小伙伴反映，我那篇文章《你最应该了解的一个物理学秘密：为什么狗撵包子走直线？》说得信息量有点大，不容易理解。我这里给自己做一个辩解：虽然最小作用量原理的表述非常的简单，但它蕴含的道理其实非常深刻，我的理解可能还不够，所以在表达上就无法说清楚。其次是，最小作用量原理是物理学原理的原理，它本身涵盖的内容实在是太宽泛了，如果单提某个方面，都不能完全代表最小作用量原理。所以，在我能力范围内实在是无法用一个简单的例子，说明涵盖物理学全领域的深刻道理。

图1 质点波动图像和波动方程

本文我尝试着，从一个崭新的角度去重新学习物理，并且以笔记的形式整理出来，跟大家分享。这篇就作为我的第一篇吧《趣谈物理与数学（函数）的关系》。我们都知道，物理里面很多定理的表述都是用数学的函数方程或者是方程组来表示的，数学和物理的关系就好像是一对情侣。谈物理就离不开数学，在分析物理和数学函数之间的关系之前，让我们先来看一下，数学的函数都是怎么工作的。

图2 y=sinx，x∈[0，2π]

抛开那些数学天才不谈，大多数小伙伴应该都是跟老郭一样，从初中开始接触函数概念的吧。在生活中遇到的各种事情，其实都有其内在的发生、发展的规律，有着随时间变化的内在因果规律的限制。如果我们能善于观察、勤于思考，我们就可以建立很多非常有趣的函数关系，这会让我们的生活充满了乐趣。从而让数学不再是一堆你不认识它，它却认识你的数字和字母组成的“天书”，这时你就会发现，数学不再是一堆冰冷的数字和概念，而是一幅色彩缤纷壮丽画卷。

图3 笛卡尔心形函数

这里我们来举一个非常有趣的例子，通过这个例子我们可以看一下，数学是如何把看似毫无关联的两个事物放在一起思考的，女生的心情好坏和男生钱包的厚度。如果女生的心情不好，则男生的钱包厚度就要减小，显然是因为男生要花钱去哄女生开心；倘若女生的心情大好，男生的钱包厚度依旧要减小，甚至男生钱包厚度的变化率更大，恐怕是因为女生开心的时候更爱购物。数学中的函数其实就是这样，当一件事情发生了变化，会引起另一件事情跟着变化，就称这两件事情之间构成了一种函数关系，两件事情之间如何相互影响，就是一个对应法则。

图4 女生的开心与男生的钱包

函数的概念

对于函数，大学里的说法是这样：设x和y是两个变量，D是一个给定的数集，如果对于每个值x∈D，变量y按照一个确定的值与x相对应，则称y为x的函数，记做y=f(x)。称x为自变量，y为因变量。称数集D为此函数的定义域，定义域一般由实际背景中变量的实际意义或者函数对应法则的要求确定。

我们从函数的定义可以看出：用数学函数可以去描述世界上的万事万物都在不断地运动变化发展过程，函数是研究运动变化的极端重要的数学模型，“变化与对应”是函数思想的核心内涵，所谓“变化与对应”的思想包括两个基本意思：其一是、世界是变化的，客观事物中存在大量的变量；其二是，在同一个变化过程中，变量之间不是孤立的，而是相互联系的，一个变量的变化会引起其他变量的相应变化，这些变化之间存在着对应关系。

图5 事件之间的变化与对应关系

函数的实例

我们把前面的例子量化：女生的心情指数作为自变量，记为x，并设定其范围为[0，10]，规定x≤3表示心情很不好，4≤x≤7表示心情一般，x≥8则表示心情很好。称相应的函数值的全体R={y|y=f(x)，x∈D}为函数的值域，我们可以把男生钱包的厚度记为y，作为因变量，它的取值范围可以是[0， ∞]，当然了实际上，即使是土豪的钱包也是不可能无穷大的，我这里就是抽象一下，为了方便接下来的讨论。这里的f叫做对应法则。对于我们前面这个例子，女生心情的好坏与男生花多少钱之间如何相互“作用”、相互“影响”，是在是太复杂了，小伙伴们都明白，本文就不讨论建立这个对应法则的过程了，因为这涉及到专业的数学建模知识。

图6 买单的男生

用函数的思想来分析物理过程

我们从前面的例子可以看出变化与对应是函数思想的核心内涵。函数不仅是贯穿于数学学习的一条主线，而且还是数学中最基础最核心的概念，也是物理学（自然科学和工程技术）上普遍使用的一个数学概念。在使用数学函数处理物理问题的时候，我们一定要牢记：因果关系是自变量与因变量的核心关系。

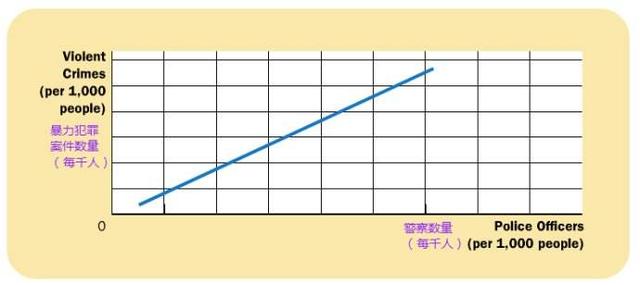
图7 变量间的因果关系

自变量是引起变化的原因，因变量是被动变化的，是变化后的结果，通常我们在使用用语言对某一个物理过程进行叙述的时候，要将因变量放在前。例如在叙述电流、电压、电阻三者间的关系时由于电压、电阻是自变量，电流是因变量要这样叙述：电阻一定时，导体中的电流与这段导体两端的电压成正比；电压一定时，导体中的电流与这段导体的电阻成反比。

对于一个实际的物理过程，引起因变量变化的自变量通常都是不只一个，遇到这种情况，研究自变量与因变量之间的关系时，数学分析上常用求偏导数的方法，物理上常用控制变量法，典型的如验证欧姆定律时就要用到控制变量法。

图8 描述电阻、电流、电压的函数

本文总结

我们关于数学函数在物理中的应用，本文就暂时写到这里，下一篇我们具体的举几个例子来对这个问题进行展开分析。从前文中我们可以看出，分析物理问题的灵魂是要抓住变与不变（或同与不同）的物理量都有哪些，然后再分析这些物理量之间的函数关系，另一方面物理以一个个具体的实例为数学提供了一个个具体的函数模型，物理以事实证明了数学的重要性与应用的广泛性。数学和物理就像是科学之树上的一对孪生兄弟，虽然各自独立发展，但是在某些领域中，你中有我，我中有你。

感谢您的阅读，我是老郭，跟您一样的科学爱好者，持续为您提供优质的科普文章。