提升初中数学（初中数学-提高篇）

三角形的三边关系为任意两边之和大于第三边，任意两边之差小于第三边。在其中一条边的角度来看，我们可以概括为三角形中任意一条边大于另外两边之差，且小于另外两边之和。对于三边关系的运用，我们通常会遇到以下几种情况。

一、判断三条线段能否组成三角形

判断三条线段能否组成三角形，需要利用三边关系。我们可以总结为以下三种方法。

（1）找出其中最长边，只需判断是否小于另外两边之和。

（2）找出其中最短边，只需判断是否大于另外两边之差。

（3）使用任意一条边，只需判断其是否小于另外两边 之和，且大于另外两边之差。

例1 下列各组分别是三根木棒的长度，其中能构成三角形的是（）

A.4 cm，7 cm，3 cm

B.2 cm，2.5 cm，5 cm

C.4.5 cm，10 cm，5 cm

D.7 cm，8 cm，9 cm

解析：根据三角形三边关系，以及上面总结的方法，可以很容易得出答案D。

二、判断三角形边长的取值范围

例2 若一个三角形的两边长分别为3 cm、6 cm，则它的第三边的长可能是（）

A.2cm B.3 cm C.6 cm D.9 cm

解析：根据三角形三边关系，对于任意一条边，大于另外两边之差，且小于另外两边之和，即大于3 cm，小于9 cm。故答案为C。

三、最值问题

1.最小值.

问题：如图，已知点A，B在直线MN的同侧，在直线MN上确定一点P，使AP BP有最小值。

作法：过A点作关于直线MN的对称点A1，连接A1和B点，与直线MN的交点P即所求（也可作B点关于直线MN的对称点，并与A点相连）,且AP BP最小值等于A1B。

证明思路：在直线MN上任取一点P1(不与P点重合)，连接AP1，BP1，A1P1，只需证明AP1 BP1>AP BP即可。

根据对称知识可知AP=A1P，AP1=A1P1。在△A1P1B中根据三边关系可知A1P1 BP1>A1B。故AP1 BP1>AP BP。

例1 在边长为4的等边△ABC中，D、E分别为BC、AB的中点，M为AD上的动点，连线BM，ME,求BM ME的最小值。

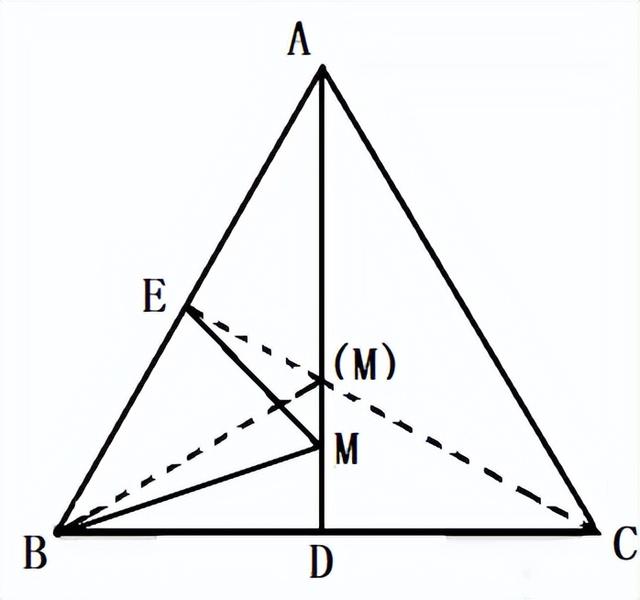
解析：根据上面总结的知识，点B关于AD的对称点恰是点C，连接C，E，与AD的交点为M，此时BM ME有最小值，且等于CE。

由已知可得BC=4，BE=2，利用勾股定理，易得CE=。

所以BM ME的最小值为。

2.最大值.

问题：如图，已知点A，B在直线MN的异侧，在直线MN上确定一点P，使PA-PB有最大值。

作法：过A点作关于直线MN的对称点A1，直线A1B与MN的交点即为所求点P,且PA-PB的最大值等于A1B。

证明思路：在直线MN上任取一点P1(不与P点重合)，只需证明PA-PB>P1A-P1B即可。

根据对称知识可知PA=PA1，P1A=P1A1，在△A1P1B中根据三边关系可知A1B>P1A1-P1B= P1A-P1B.又因为A1B=PA1-PB=PA-PB，故PA-PB>P1A-P1B。

例2 如图所示，一次函数y=x 3的图象与反比例函数y=的图象交于A，B两点，在y轴上确定一点P，使PB-PA有最大值，求此时P点的坐标。

解析：易求出A(-2,4)和B(8,-1),根据上面总结的规律，作A点关于y轴的对称点A1(2,4),直线A1B与y轴的交点即为所求的点P。根据A1和B点的坐标可求出直线A1B的解析式，并易求得与y轴的交点P(0,)。