锐角三角形垂线交点的性质（锐角三角形一条边和另外两边上高的垂足连线交点）

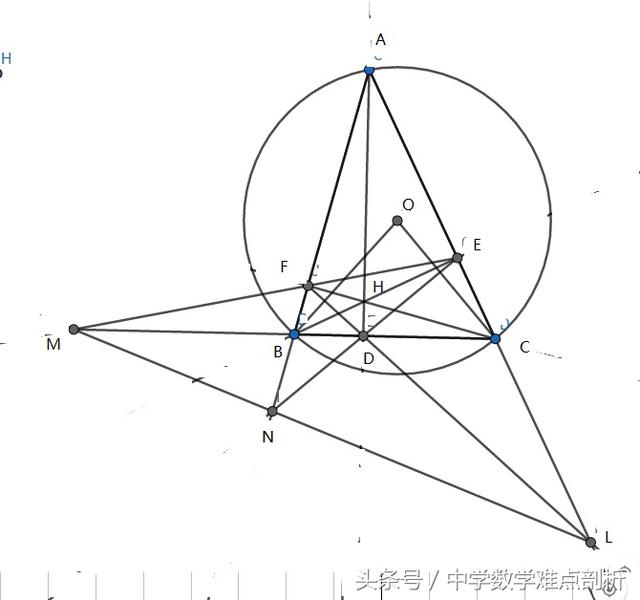
如图三角形ABC 中，AD、BE、CF分别是BC、AC、AB上的高，O为三角形外心，H为垂心 M为BC延长线和EF延长线的交点，N为AB延长线和ED延长线的交点，L为AC延长线和FD延长线交点。连接MN 和NL

则：1、OB⊥FD、OC⊥DE、OA⊥EF

2、连接OH，则OH的中点K为三角形DEF的外心；

3、OH⊥MN 、OH⊥NL ， L、M、N三点共线

提示：1、在B点作圆O的切线BT，可以证明FD∥BT

2、取BC中点A1，可证明E、F、D、A1四点共圆 ：∠DEF=∠DEB ∠BEF=∠DAB ∠BCF=90-∠ABC （90-∠B）=2（90-∠ABC）=2∠BCF=∠DA1F OA1⊥BC，AD⊥BC，K在DA1的中垂线上。证明K为三角形DEF外心。

3、BDEA四点共圆得NB*NA=ND*NC，得N在圆O和圆K的根轴，同理得M、L也在两圆根轴上，OK⊥NL， OK⊥MN，三点共线。