怎么知道机械振动的频率（振动是怎么产生的）

机械振动是一种特殊形式的运动，物体相对于平衡位置所作的的往复运动称为机械振动，是指机械系统的位移、速度、加速度在某一数值附近随时间的变化规律。例如，机器箱体的颤动、管线的抖动、叶片的摆动等都属于机械振动。

产生振动是因为它本身具有质量和弹性，而阻尼抑制振动。当机械系统受到外力作用时，质量吸收动能，获得速度；质量本身离开平衡位置后具有一定得势能，也必然产生指向平衡位置的恢复力；而弹簧是迫使质量回到原来的平衡位置主要恢复力。这种能量的转换导致了机械振动，若失去外力作用，由于阻尼的存在，振动将逐渐消失。

质量，表示物体保持其原始的静止或运动状态的惯性。力促使静止或运动状态发生变化，质量阻止这种变化,Kg 。

刚度，使结构弯曲即挠曲一定的距离需要一定的力。产生一定挠度所要求的力的量值被称为刚度，N/m。

阻尼，一旦力使一个零件或结构进入运动状态，零件或结构就会具有减慢运动（速度）的固有机制。这个降低运动速度的性质称为阻尼，N/(m/s)

机器中的由缺陷引起的振动，如果缺陷引起的振动比以上三个抑制性质的净和大很多，产生的振动值就会很高。

需要说明的是，物体并非受到激励就会振动，因物体运动过程中总会受到阻尼作用，只有阻尼小于临界值时才会产生振动，临界阻尼为物体的固有属性。

临界阻尼：任何一个振动系统，当阻尼增加到一定程度时，物体的运动是非周期性的，物体振动连一次都不能完成，只是慢慢地回到平衡位置就停止了。当阻力使振动物体刚能不作周期性振动而又能最快地回到平衡位置的情况，称为“临界阻尼”。

实际阻尼与临界阻尼之比称为阻尼比。当阻尼比小于1时，振动振幅按指数规律衰减；当阻尼大小于1时，物体不会振动，而是做非周期运动。

一、简谐振动

简谐振动是一种最基本的振动形式，了解它的特性，对了解其它振动的特性和掌握振动监测诊断技术都是十分重要的。简谐振动的一般数学表达式为：

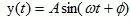
式中：y（t）——振动体相对于平衡位置的位移

A——振幅，表示振动体偏离平衡位置的最大距离

ω——振动的角频率，表示2π秒内振动的次数或圆频率（ω=2πf，f=1/T，f为振动频率，T为振动周期）

φ——振动的初相位角，用以表示振动物体的初始位置。

简谐振动是一种确定性振动，其特性决定于A，ω，φ三个参数。振幅A表示振动的大小，角频率ω表示振动的快慢，初始相位角φ表示振动物体的初始位置。这三个参数在设备诊断中有着重要的意义。

需要指出的事，简谐振动一定是周期振动，但是，周期振动不一定是简谐振动。简谐振动的位移、速度、加速度三者之间波的形状相似，频率(或周期)完全相同，不同之处在于幅值和相位，加速度领先速度90º; 速度领先位移90º，（因平台内不能编辑公式，位移、速度、加速度公式略过）

即、速度振幅是位移振幅的ω倍；加速度振幅是位移振幅的ω²倍；振动频率越高，三者之间的差别就越大。加速度的大小与位移成正比，而其方向与位移相反，加速度的方向始终指向静平衡位置。

根据简谐振动这一性质可导出一个简易公式， 由于生产现场使用振动表位移量表示为峰峰值、速度表示为有效值、而加速度表示为峰值，所以同频下位移与速度幅值可用下式进行换算，并以此识别频率特征：

式中：_——位移峰峰值(μm)，_——速度有效值(mm/s)，—转速频率(HZ)

例：假如一台每分钟1500转的风机以单一的工频振动，现场实测位移峰峰值是90μm，那它转频振动速度有效值应该是5mm/s，如果实测速度有效值是8.6mm/s，则实测值远大于5mm/s，说明高频振动对故障起主导作用；若振动位移峰峰值同样是90μm，而实测速度有效值是3mm/s，则实测值小于5mm/s说明低频振动对故障起主导作用。

设备的实际振动并不是单一的简谐振动，往往由多种频率成分构成，但对于基频故障来说，转速频率往往占有绝对大幅值，其换算结果基本与上公式相符合。