中考数学最值问题技巧（聚焦中考最值问题之构造与转化）

数学思想方法是数学教学的灵魂，是数学知识的精髓，是把数学知识转化为能力的桥梁，而转化思想是数学思想的核心。它是从未知领域发展，通过数学元素之间的因果联系向已知领域转化，从中找出它们之间的本质联系，以达到解决问题的一种思想方法。在初中数学中，主要表现为数学知识的某一形式向另一形式转变，即化新为旧、化繁为简、化曲为直、化数为形等。

转化一般可分为两类，一类是具体的转化，即通过定理或者性质将条件转化和结论转化；另一类是思维转化，这类一般对学生思维要求较高！为了实施有效的化归，既可以变更问题的条件，也可以变更问题的结论，既可以变换问题的内部结构，又可以变换问题的外部形式，既可以从代数的角度去认识问题，又可以从几何的角度去解决问题。

构造的方法就是数学中的概念和方法按固定的方式经有限个步骤能够定义的概念和能够实现的方法。常见的有构造函数，构造图形，构造恒等式。平面几何里面的添辅助线法就是常见的构造法。构造体现转化思想的最终体现方式，构造法解题有：直接构造、变更条件构造和变更结论构造等途径。

应用举例

1．如图，在平面直角坐标系xOy中，直线AB经过点A（﹣4，0）、B（0，4），⊙O的半径为1（O为坐标原点），点P在直线AB上，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（　　）

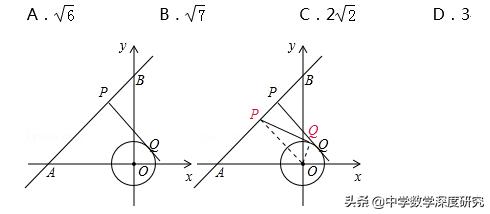
【解析】连接OP、OQ．∵PQ是⊙O的切线，∴OQ⊥PQ；

根据勾股定理知PQ2＝OP2﹣OQ2，

∵当PO⊥AB时，线段PQ最短；

又∵A（﹣4，0）、B（0，4），∴OA＝OB＝4，

2．如图，⊙O的直径为4，C为⊙O上一个定点，∠ABC＝30°，动点P从A点出发沿半圆弧AB向B点运动（点P与点C在直径AB的异侧），当P点到达B点时运动停止，在运动过程中，过点C作CP的垂线CD交PB的延长线于D点．

（1）在点P的运动过程中，线段CD长度的取值范围为　 　．

（2）在点P的运动过程中，线段AD长度的最大值为　 　．

【解析】（1）如图1中，∵AB是直径，∠ABC＝30°，AB＝4

∴∠ACB＝90°，∠A＝∠P＝60°，AC＝2，

∵CD⊥PC，∴∠PCD＝90°，CD＝PC•tan60°，

∵PC的最小值＝AC＝2，PC的最大值为直径＝4，

∴CD的最小值为2√3，最大值为4√3，∴2√3≤CD≤4√3．

故答案为2√3≤CD≤4√3．

（2）如图2中，∵在Rt△PCD中，∠PCD＝90°，∠P＝60°，∴∠PDC＝30°，

∴点D在以BC为弦的⊙O′（红弧线）上运动，

∴当A、O′、D共线时，AD的值最大．连接CO′、BO′．

∵∠BO′C＝2∠CDB＝60°，O′C＝O′B，

∴△O′BC是等边三角形，∴BO′＝BC＝2√3，∠CBO′＝60°，

∵∠ABC＝30°，∴∠ABO′＝90°，

3.如图，已知Rt△ABC中，∠A=90°，AC=3，AB=4，点P为AB边上一动点，连接CP，过点P作PM

CP，交BC于点M，则BM的最大值为____________.

【解析】要求BM的最大值，发现点M随着点P的运动而运动，反过来思考，一个点P对应一个点M，那么也可以由点M来确定点P，所以本题的问题就转化为"在BC边上找一点P，使得∠MPC=90°，接下去利用圆的知识解决，只需考虑临界情况，即以MC为直径的圆恰好与AB相切时，CM最小，即BM最大。

如图，设PO=OC=r，BO=5-r。

4．（2019秋•雁塔区校级月考）仔细阅读，解答下列问题

（1）有一长方体的食物包装纸盒如图（1），已知长方体的底面长为12，宽为9，高为5，一只蚂蚁想从底面A处爬到B处去吃食物，请问：蚂蚁爬行的最短距离是多少？

（2）如图（2），圆柱形容器的高为1.2米，底面周长为1米，在容器内壁离容器底部0.3米的点B处有一只蚊子，此处一只壁虎正好在容器外壁离容器上沿0.3米与蚊子相对的点A处，求壁虎捕捉到蚊子的最短路程是多少？（容器厚度忽略不计）．

【解析】（1）第一种情况：把我们所看到的前面和上面组成一个平面，．

则这个长方形的长和宽分别是12cm和14cm，

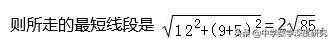
第二种情况：把我们看到的左面与上面组成一个长方形，

则这个长方形的长和宽分别是9cm和17cm，

第三种情况：把我们所看到的前面和右面组成一个长方形，

则这个长方形的长和宽分别是10cm和4cm，

三种情况比较而言，第一种情况最短，

∴蚂蚁爬行的最短距离是2√85cm；

（2）如图：∵高为1.2m，底面周长为1m，在容器内壁离容器底部0.3m的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿0.3m与蚊子相对的点A处，∴A′D＝0.5m，BD＝1.2m，

∴将容器侧面展开，作A关于EF的对称点A′，

连接A′B，则A′B即为最短距离，

答：壁虎捕捉到蚊子的最短路程是1.3m．

5．（2019秋•金水区校级月考）数与形是数学中的两个最古老，也是最基本的研究对象，它们在一定条件下可以相互转化，数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过"以形助数"或"以数解形"即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的．

（1）【思想应用】已知m，n均为正实数，且m n＝2，

通过分析，爱思考的小明想到了利用下面的构造解决此问题：如图，AB＝2，AC＝1，BD＝2，AC⊥AB，BD⊥AB，点E是线段AB上的动点，且不与端点重合，连接CE，DE，设AE＝m，BE＝n，

①用含m的代数式表示CE＝　　，用含n的代数式表示DE＝　　；

而CE DE≥CD（当且仅当C、E、D共线时取等号），

作DH⊥CA交CA的延长线于H，如图，易得四边形ABDH为矩形，

∴AH＝BD＝2，DH＝AB＝2，

6．如图，已知正方形ABCD的边长为4，点P是AB边上的一个动点，连接CP，过点P作PC的垂线交AD于点E，以PE为边作正方形PEFG，顶点G在线段PC上．对角线EG、FP相交于点O．

（1）若AP＝3，求AE的长；

（2）连接AC，判断点O是否在AC上，并说明理由；

（3）在点P从点A到点B的运动过程中，正方形PEFG也随之运动，求DE的最小值．

【解析】（1）只要证明△APE∽△BCP，可得AE/BP=AP/BC由此即可解决问题；

（2）点O在AC上．过点O分别作AD、AB的垂线，垂足分别为M、N，只要证明△OME≌△ONP，可得OM＝ON；

（3）利用相似三角形的性质构建二次函数即可解决问题；

7．如图1，抛物线y＝﹣1/2x2 3/2x 2与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，连结BC．

（1）求直线BC的解析式；

（2）如图2，点D是CB上方抛物线上一动点，连结DC，DB，过点A作CB的平行线，交对称轴于点E，交DB的延长线于点F，连接CF，当△CDF的面积最大时，在对称轴上找一点R，使得DR 2√5/5RE的值最小，求出此时点R的坐标；

【解析】（1）利用待定系数法求出B、C两点坐标即可解决问题；

（2）如图2中，连接OD，作DH⊥AF于H，RQ⊥AF于Q，DH交对称轴于R′．由AF∥BC，推出S△BCF＝S△ABC＝定值，由S△CDF＝S△BCD S△BCF，

直线DH的解析式为y＝2x﹣1，R′（3/2，2）．

8．（2019•清江浦区一模）问题提出：如图1，在Rt△ABC中，∠ACB＝90°，CB＝4，CA＝6，⊙C半径为2，P为圆上一动点，连结AP、BP，求AP 1/2BP的最小值．

（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB上取点D，使CD＝1，则有CD/CP=CP/CB=1/2，又∵∠PCD＝∠BCP，∴△PCD∽△BCP．∴PD/BP=1/2，∴PD＝1/2BP，∴AP 1/2BP＝AP PD．

请你完成余下的思考，并直接写出答案：AP 1/2BP的最小值为　　．

（2）自主探索：在"问题提出"的条件不变的情况下，1/2AP BP的最小值为　　．

（3）拓展延伸：已知扇形COD中，∠COD＝90°，OC＝6，OA＝3，OB＝5，点P是弧CD上一点，求2PA PB的最小值．

【解析】（1）如图1，连结AD，

∵AP 1/2BP＝AP PD，要使AP 1/2BP最小，

∴AP AD最小，当点A，P，D在同一条直线时，AP AD最小，

即：AP 1/2BP最小值为AD，

在Rt△ACD中，CD＝1，AC＝6，

∴由勾股定理可求得AD＝√37，

AP 1/2BP的最小值为√37，故答案为：√37；

（2）如图2，连接CP，在CA上取点D，使CD＝2/3，

∴CD/CP=CP/CA=1/3，

∵∠PCD＝∠ACP，∴△PCD∽△ACP，∴PD/AP=1/3，

∴PD＝1/3AP，∴1/3AP BP＝BP PD，

（3）如图3，延长OA到点E，使CE＝6，

∴OE＝OC CE＝12，连接PE、OP，

方法总结

万法归宗：构造完成的目标图形：

路径成最短，折线到直线。所求路径在一般情况下是若干折线的组合，这些折线在同一直线上时即为最短路径）

基本图形：动点有轨迹，动线居两边。动点轨迹可以是线或圆，动线指动点与定点或定线、定圆的连线，动线与折线同指）

核心方法：同侧变异侧，分散化连续。

动线在同侧进，要变为异侧，一般用翻折、三角、相似的方法构造；动折线被定长线段分散时需化为连续折线，一般用平移的方法构造。

,