鸡兔同笼计算法图解（数学思考鸽笼原理）

一个简单的原理

像数学家一样思考！

鸽笼原理，又名狄利克雷抽屉原理、鸽巢原理。

1）表述为：

• 若有n个笼子和n 1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子有至少2只鸽子。

2）表述为：

• 若有n个笼子和kn 1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子有至少k 1只鸽子。

集合论的表述如下：

• 若A是n 1元集，B是n元集，则不存在从A到B的单射。

拉姆齐定理是此原理的推广。

鸽巢原理指出，如果n项放在为m的容器，其中n> m，则至少一个容器必须包含多个项。

据信，第一个鸽子洞概念的形式化是由狄利克雷（1805-1859）提出的。当狄利克雷用德语和法语出版作品时，他会交替地称之为“舒巴赫原理”和“提洛瓦原理”，两者都翻译成“抽屉”。然而，由于狄里克利特的父亲是一名邮政局局长，人们认为他所指的抽屉最好翻译成英语为“鸽巢”，例如那些常用于存储和分类邮件的抽屉。“鸽巢原理”这一术语的首次出现是由数学家拉斐尔罗宾逊在1940年使用。

无限集

格奥尔格·康托尔（1845-1918）在1873-74年对可数性的研究中，间接运用了鸽巢原理:

由于实际原因，让我们通过想象一个有100个座位的教室来说明有限情况。在坐满学生的情况下，我们可以推断出一组学生的人数与一组座位的人数之间的关系。如果座位是空的，那座位就比学生多。如果没有空位，一些学生站着，那么学生集合的大小要大于座位的集合大小，以此类推。 ——节选自维斯达尔(2018)的《无限与超越的本质》

虽然这是一个非常简单且容易理解的概念，但鸽子洞原理却足以证明那些远非显而易见的事实。从某种意义上说，鸽巢原理是最典型的计数参数之一，它允许我们证明如下语句:

• 在任何时候，至少有两个人的头上有相同数量的头发;
• 不能用尺寸为1 x 2的多米诺骨牌覆盖8 x 8正方形棋盘；
• 在一个367人的房间里，至少有两个人生日相同;
• 任何使一些输入更小的无损压缩算法也会使一些输出更大;

形式上，想到的鸽巢原理作为关于功能的语句˚F从域P→PH，其中鸽Ñ飞入归档˚F（Ñ），如下面所示：

A：比鸽笼更多的鸽子| n | > | f（n）|。

B：与鸽笼相同数量的鸽子| n | = | f（n）|。

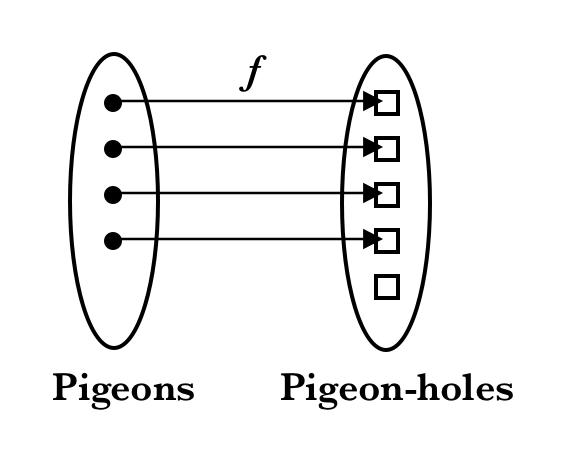
C：鸽子比鸽子更多| n | <| f（n）|

这三个例子说明了从(“鸽子”)到上(“鸽子洞”)的三种函数类型，它们可以相互映射:

• A：如果| n | > | f（n）|，那么函数是非内射射影函数（不是双射）
• B：如果| n | = | f（n）|，那么函数是一个内射射影函数（双射）
• C：如果| n | <| f（n）|，那么该函数是一个内射非射影函数（不是双射）。

情况A是说明鸽子原则的本质的情况，即如果你将n个物品放入m个容器并且n > m，那么至少一个容器必须包含多个物品。因此，将鸽子映射到鸽巢的函数f称为射影函数。我们可以通过矛盾轻松证明这一原则：

鸽巢原理证明 假设总共有n只鸽子放入m个鸽子洞和n个>个鸽子洞中，假设不存在至少有n/m只鸽子的鸽子洞，即每个鸽子洞的鸽子数小于n/m: 每个鸽子洞内的鸽子数量< n/m 鸽子数< m×n/m 鸽子数量< n 但是，假设鸽子的数量严格等于n，我们得到了一个与我们假设的相反的结果，即每个鸽子洞的鸽子数量都小于n/m。因此，至少存在一个鸽子洞，鸽子数量至少为n/m。

正如上面提到的，尽管很容易理解，鸽巢原理允许我们证明那些有时看起来不可知的陈述。比如：

示例A - 大数据中的公共属性

在任何时候，至少有两个人的头上有相同数量的头发

为了证明这一点，我们需要确定两个事实。首先，人类肯定超过60亿。其次，这是一个生物学的客观事实，每个人头部的头发少于一百万（通常，数量范围在90,000-150,000之间）：

例A的证明 设A是所有人的集合，B ={0,1,2,3,4，…一个人头上可以长多少根头发就有多少根。设f是一个映射a→B的函数，其中f(x)等于x头上的毛发数。由于| a |>|B|，鸽巢原理断言f不是单射的。因此有两个人x和y ，f(x) = f(y)这意味着他们头上的头发数量相同。

例B-数字集合

如果A是1到100之间的10个整数的任意集合，那么必须存在两个不同的子集X和Y，其中X中的元素之和等于Y中元素的总和。

考虑例如随机集A = {6,7,11,12,17,50,51,80,90,100}，其具有子集X = {7,12,17,50}并且Y = {6,80其中X中元素的总和等于Y中的元素之和，即86.如果我们试图通过改变A中的值（比如将7更改为5）来弄清楚这一点，我们会得到A '= {5,6,11,12,17,50,51,80,90,100}但仍然找到子集W = {6,12,17,50}和Z = {5,80}，其基数为都等于85。

实施例A的证明 假设A⊆{1,2,3,4，...，99,100}和| A | 请注意，如果X⊆A，则X不超过10个元素，每个元素在1和100之间。因此，X的所有元素之和小于100×10 = 1000.考虑函数f： （A）→{0,1,2,3,4，...，1000}其中f（X）是X中元素的总和。 作为|（A）|的基数。=2¹⁰= 1024> 1001 = | {0,1,2,3，...，1000} | 从鸽子原理出发，f不是单射的，即它是一种“多对一”的功能。 因此，存在两个不等的集合X，Y∈（A），其中f（X）= f（Y）。换句话说，存在子集X⊆A和Y⊆A，其中X中的元素之和等于Y中元素的总和。

例C - 中国剩余定理（中国余数定理）

著名的中国余数定理给出了多个方程有一个同时整数解的必要条件。可以表述为：

设m和n为相对正整数。然后系统x = a（mod m），x = b（mod n）有一个解。

中国余数定理是有用的，因为它建立了如果我们知道一个整数n除以几个整数的余数，那么我们可以唯一地确定n除以这些整数的乘积的余数。早在三世纪，中国数学家孙子就提出了这个著名的定理:

有些东西的数量是未知的。如果我们用3来数，就剩下2个;到5时，还剩下3个;到7时，剩下2。有多少东西?

要实际地说明这一点，请考虑一盒冷硬币。我们知道，如果把硬币平均分配给六个朋友，就会剩下四个硬币。如果把硬币平均分给五个朋友，就剩下三个硬币。如果盒子里有满足这些条件的最小数量的硬币，那么当七个朋友平分时，还剩下多少硬币?答案是零。

例C的证明 首先考虑序列 (1) b, b m, b 2m，…， b (n - 1)m 序列形成一个完整的剩余类modulo n。 (2) 0, m, 2m, 3m，…(n - 1)m 由于(m,n)的最大公约数= 1，所以有xm≡ym (mod n) <=> x≡y (mod n)，因此序列(2)中的每个元素都是唯一的。向序列(1)中添加b只会循环地破坏剩余类。 根据鸽巢原理，对于任意0≤a < n，对于任意k∈{0，…n−1}。

建设性与非建设性证明

最后，对分类证明的类型作了说明。鸽巢原理证明虽然有用，但其定义特征是它们是非建设性的，也就是说，尽管它们证明了某物的存在，但它们不能提供一个明确的例子来证明定理。为了说明这种差别，考虑对同一命题的两种证明，即:

存在无理数x，y，其中xʸ是有理数。

让我们首先考虑一个非建设性的证明，它表明存在无理数x和y，其中xʸ是有理数，而不是实际产生一个例子：

非建设性证明 令x =√2^（√2）且y =√2。我们知道y是无理数，但我们不知道x是不是。如果x是无理数，那么我们有无理数的无理幂就是有理数： xʸ=（√2^（√2））^（√2）=（√2）^（√2×√2）=（ √2）²= 2 如果x是有理的，那么 yʸ=√2^（√2）= x是合理的。 不管怎样，我们都有一个无理数的无理数次方，是有理数。

接下来考虑一个替代的，建设性的证据：

建设性证明 设x =√2且y = log（9）。然后 xʸ=√2^（log（9））=√2^（log（3²））=√2^（2log（3））=（√2^ 2）^（log（3））^ = 2 ^ （log3）= 3 由于3是有理数，我们已经证明xʸ= 3是有理数。 我们知道x =√2不是有理数。我们不知道y = log（9）是否是有理数。假设log（9）是有理数的，因此有两个整数a，b，其中a / b = log（9）。然后2 ^（a / b）= 9，所以2 ^（a / b）ᵇ=9ᵇ，减少到2ᵃ=9ᵇ。但是，我们知道2ᵃ是偶数，9ᵇ必须是奇数，所以它们不能相等。我们得到了一个矛盾，必须假定对数（9）是无理数。

在上述对同一命题的证明中，在构造证明的过程中，我们还提供了一个命题为真的例子，即x =√2,y = log(9)。这一点，我们永远不能单独从鸽子洞和其他非建设性的证明中得到。

,