一元二次方程式公式解法（求解一元二次方程式不再繁琐）

二次方程式是古老的数学公式，其历史可以追溯到公元前2000年的古代巴比伦人。它最初是被用来计算涉及长度可能变化的矩形问题的方法。它是一个“多项式方程”，意味着它始终有两个有效解。

在典型的二次方程式X^2-BX C = 0中，学生们会尝试根据经验法则求出X的两个不同解：B的值应等于两个不同解值的总和，而C则等于两个解值相乘的结果。

这条规则给了学生们一个大致的框架，当前大多数学生都会使用猜测和校验方法进行求解，在该方法中，他们对答案可能落在什么范围内进行有根据的猜测，然后计算其猜测是否真正有效。

现在卡内基梅隆大学的一位教授为全球正在学习代数的学生带来了一个好消息，他提供了一种更简单有效的方法，来解决涉及二次方程的问题。

这个新方法是罗博深博士在指导参加美国数学奥林匹克竞赛的初中生，打算编写一些涉及二次方程的试题时无意中发现的。他的方法包括应用一个简单得多的方程来求解二次方程中的一个变量，而不必进行通常很繁琐的整个方程的计算。

罗伯森博士制作了一段视频解释他的发现，他对于当时自己的发现说：“我都惊呆了，我以前怎么没见过这个解法，我在任何教科书里都没见过”。

最初他不敢相信他是第一个发现这种新方法的人，于是他仔细查找了数学史上有关二次方程式的资料，反复核对了古巴比伦和古印度的相关数学文本。

二次方程式之所以这么难解的部分原因在于，它不是只有一个答案，而是两个答案，用数学术语来说就是多项式方程。由于学生们在尝试求解方程式时，必须确保他们的答案对于两个不同的数字都适用，所以大多数人最终会借助于一种劳动密集型的猜测和检查方法，即学生们将数字代入方程，看看它们是否可行。

对于罗博深博士而言，学生们的做法有些与数学精神背道而驰，数学算法本质上是将“本来应该复杂的事情简化为简单的事情”的学问。

那么卡内基梅隆大学的罗博深博士的新方法究竟有什么不同，恐怕你已经等不及了，现在让我们看看下列几张图, 为什么我们说它更简单更好计呢？

罗博士的解题思路主要从从X^2-BX C = 0中的B值开始，而不是针对C进行因式分解。针对方程式中的B，上图中2个解的值的总和是8，那么这2个数值应该距离平均值相等。所以可以用4-U 和4 U进行表述，U代表未知数。

而这2个数的乘积应该等于12，所以（4-U)*(4 U)=16-U^2=12, 于是U^2=4, 进而计算出U= 2或-2，最后可以算出2个数值就是2和6。

他的发现可以让运算简化，这样其他猜测工作就无关紧要了。

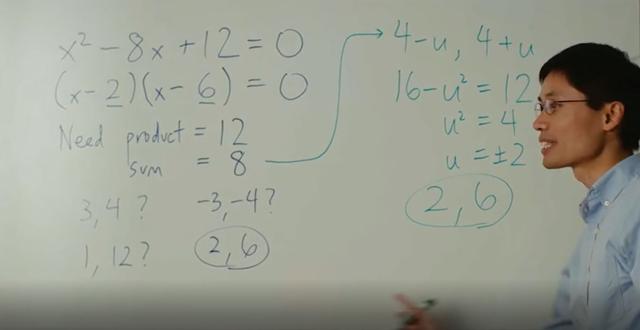
罗博深博士总结说：由于该方法从总和开始解决问题，因此可以用来求解任何二次方程式。下面两个图片应用了同样的运算方式。

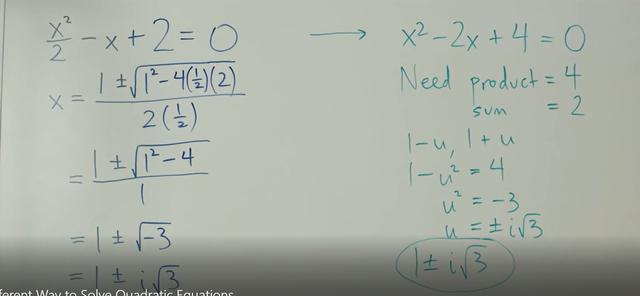
这样的新算法是不是很好理解，很容易计算呢？对于他的发现，罗博士想与世界尽可能地广泛分享，因为至少它可以揭开一个数学复杂运算中的神秘面纱，而这个方程式让很多人头疼，觉得数学并不适合他们。

最后他说：“我认为，如果能够证明数学实际上是一门仍然可以让每个人欣赏的学科，那这个发现是非常有用的。数学实际上是很美的。”