数学家是怎样研究东西的（数学家如何思考无穷）

作者 | 雷勇

本文首发于2019年2月《科学画报》新知版

小时候，小朋友们比赛互相喊一个更大的数，最后总有小朋友喊“无穷大”。无穷，不细想的话，感觉很熟悉。记得上次跟一位学物理的同事谈起无穷问题，我跟他聊了下康托尔的无穷基数，他听后的评价是“我咋觉得这么‘唯心’呢”。由此也看出，无穷其实非常的抽象，看不到摸不着，它只存在于我们的心智之中。最近刚刚读了美国布朗大学数学教授、数学科普作家理查德·伊万·施瓦茨的《无穷的画廊》一书，他让抽象的无穷以尽可能实在的方式呈现在我们面前。

《无穷的画廊》用简洁明了的语言，将数学集合理论丝丝入扣但又栩栩如生地展现在读者的面前。绘制卡通是作者的爱好，他的简洁而饱含逻辑和哲理的文字，辅以漂亮而又富有生趣的卡通，与集合论抽象的概念、符号和公式巧妙结合，浑然构成一个整体，如一个视觉的画廊，又如一个充满悬念而富有挑战的思想侦探。这确实带给我们一种惊喜。孙小淳与王淑红两位教授把它翻译成中文，为大家阅读该书进一步提供了便利。

其实人们在数学上最早接触无穷多是从

开始的，孩子们很难理解与1是相等的，总觉得即使再循环也还差那么一点点。尽管老师给出分数或者方程等解释方式，但心中的困惑却无法消除。

我们见到的对无穷的困惑最早来自古希腊数学家芝诺，他提到这样一个问题。

“阿基里斯（又名阿喀琉斯）是古希腊神话中善跑的英雄。在他和乌龟的竞赛中，他的速度为乌龟的十倍，乌龟在前面100米跑，他在后面追，但他不可能追上乌龟。因为在竞赛中，追者首先必须到达被追者的出发点，当阿喀琉斯追到100米时，乌龟已经又向前爬了10米，于是，一个新的起点产生了；阿喀琉斯必须继续追，而当他追到乌龟爬的这10米时，乌龟又已经向前爬了1米，阿喀琉斯只能再追向那个1米。就这样，乌龟会制造出无穷个起点，它总能在起点与自己之间制造出一个距离，不管这个距离有多小，但只要乌龟不停地奋力向前爬，阿喀琉斯就永远也追不上乌龟！”

人们都觉得他说的是错的，但是又找不到角度反驳他。

其实所有的这些困惑，都是因为人们对无穷的理解不够准确，没有意识到有限和无限存在着巨大的差别。《无穷的画廊》这本书就是试图引领着读者揭示无穷的秘密。

书里先从一一映射开始讲起。两个有限集合里面的元素个数，我们很容易比较多少。但是两个无限集里面的元素个数的多少就无从比较。简单地认为无限集里面的元素个数相等，是没有依据和不负责任的。解决无限集中元素个数多少的问题，借助的工具就是一一映射。作者举了两个例子：

“在一场音乐会上，是人多还是椅子多？只要让每人挑一把椅子坐下，看看是剩下椅子还是有的人没有座位。”

“是口香糖多还是孩子多，真的数数太麻烦了，只需要给孩子每人发一块口香糖，看看是剩下了口香糖，还是有孩子没有吃到糖。”

这里的数学思想就是让两个集合中的元素，通过某种方式建立一个对应关系，这可以帮助我们判断两个集合中元素个数的多少。如果两个集合中的元素是一对一建立起来的一个对应关系，就是一一映射。当然，这在有限集合中看起来不是那么的重要，但是在无限集中就显得非常关键。

对于正整数集合和负整数集合，这两个集合可以建立一个一一映射关系。也就是说，每一个正整数与它的相反数一一对应，于是我们知道正整数的个数跟负整数的个数应该是一样的。作者却用一只有无数颗牙的小鸡（为什么会是小鸡？小鸡真的有牙吗？），提出了这样一个问题。让正整数集合与正偶数集合建立一个一一映射关系，

按前面的想法，正整数的个数应该与正偶数的个数相等。这一点超出了我们正常的感受范围，所以当时的数学家们看到这个观点也并不认可。当时的大数学家庞加莱也认为，这个推导可能存在某些问题，总之它是不正确的。实际上这正是无穷自身的魅力所在，这也再一次说明了有限和无限有着巨大的差异。作者在书中评价道，“康托尔所做的就是推广了大小的概念，把大小从有限的数字王国推广到了无限”。

接下来，作者又图文并茂地说明了整数的个数跟正整数的个数相等；有理数的个数也跟正整数的个数相等，自然也就跟偶数的个数相等。

值得一提的是，作者在前文的讲述中顺带着讲解了自然数用集合论定义的方法，而这种方法是我在大学毕业几年后才知道的。感慨的是，该书的缘起是作者为了教小女儿学习数学而作，我的想象中作者的女儿应该不大。看来无论多“高深”的数学知识，只要讲述方法得当，就可以让人易于接受。

通过前面内容，读者往往会想，是不是所有的无限集合中的元素个数都跟整数的元素个数相同？因此，该书的后半部分基本都在讨论这个问题。

书中构造了一个“二进制串”，如图1，把一行中的无限个格子每个都染成白色或者黑色。

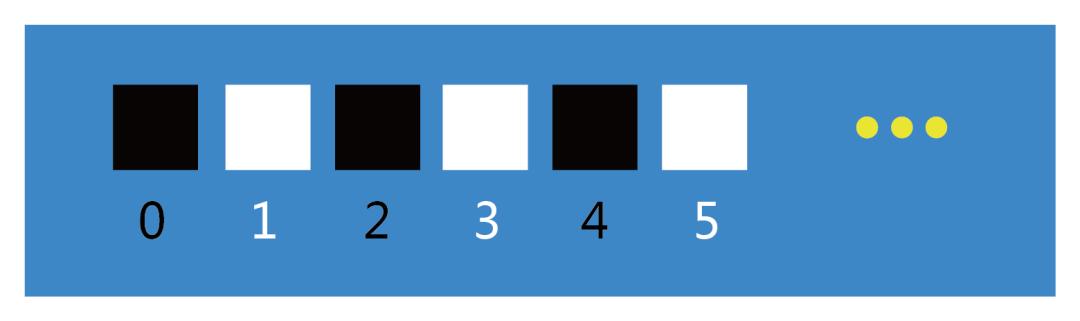
图1

因为格子的个数有无穷多个，因此染色方式也有无穷多种，这样我们把用各种不同染色方式染色后的每行格子从上到下依次排列，如图2。

图2

这样的话，我们就可以让它的行数与相应行的染色方式构成一个一一映射，我们可以想象，每一个非负整数都与“不同染色方式的行”对应。正当我们认为格子不同的染色方式的数量与正整数个数相同的时候，却发现了一个意外。

图3

作者说，“想象你沿着这张表的对角线行走，并同时记录下你看到的颜色”。也就是从上至下依次记录下对角线上的每一个格子的颜色，如图4所示：

图4

调换上面格子的颜色，即原来是黑色的调换成白色，原来是白色的调换成黑色（如图5）。那么，这一行就如同幽灵般的存在，因为它不属于图中的任意一行，作者把新构造的这一行叫作Bob。

图5

Bob不可能是第0行，因为它与第0行的第1个格子颜色不同；Bob也不可能是第1行，因为它与第1行的第2个格子颜色不同；Bob也不可能是第2行，因为它与第2行的第3个格子颜色不同；以此类推。结论是Bob不是这张表中的任何一行。

前面的格子包含了所有的不同染色方式，而Bob却不在其中，这显然是矛盾的。矛盾的产生就来自这两个无穷的大小是不同的。数学上称这两个集合没有相同的“基数”。这就是说，无穷的基数不止一个。

后面部分作者用了一定篇幅构造了实数与二进制串的一一映射关系，也就是说，实数集与二进制串有相同的基数，同时还说明了实数集合与正整数集合的大小是不同的。

全书初看起来觉得简单，但里面蕴含着丰富的数学思想，在一一映射的构造上技巧独到，思维的火光迸射出耀眼的光芒。作者虽是领着孩子探求康托尔的思维轨迹，但是里面也有很多作者自己非常独到的见解。作为数学专业的毕业生，我读起来也收获颇丰。

数学家康托尔是为我们揭示无穷秘密的第一人，今年是他逝世100周年，译者想借此向康托尔致敬。本书用来阐述康托尔集合论思想的事例都来自现实生活，充满童心和爱心，使生活的意境与丰富的想象完美结合。而且全书虽以卡通的形式呈现，却富含哲理，说明数学与我们的生活和思维方式有着意想不到的奇妙联系。这样富有创意和灵动的作品实属罕见，对于传播数学文化有着非常大的价值。

☞点击下面的链接购买《无穷的画廊》

传播数学，普及大众

长按识别二维码关注我们

欢迎把我们推荐给你身边的朋友

▼

▼▼▼点击阅读原文发现更多好玩的数学。

,