matlab中微分方程的数值解（MATLAB微分方程数值解法的刚性问题）

若解函数并不是平滑的，则在求解的时候渐变处会有很多数值求解点，这会导致MATLAB中的ode45方法求解时间增长，这就是刚性问题，需在渐变处减少求解点，以加快求解速度。

使用ode45和ode15s计算，对比求解时间即可判断是否为刚性问题,s代表自适应变步长求解。

% syms y(x) %数值解，不用符号变量

y0=[2,0];%y和diff(y)的初始值

tspan=[0,500];%积分区间

opts=odeset('RelTol',1e-2,'AbsTol',1e-4);

tic

[x,y]=ode45(@ode7,tspan,y0,opts)%y为两列，表示位置和速度,计算时间2.72

toc

tic

sol=ode15s(@ode7,tspan,y0,opts)%增加收敛性，计算时间0.0214

toc

tic

sol=ode23s(@ode7,tspan,y0,opts)%增加收敛性，计算时间0.0214

toc

tic

sol=ode23t(@ode7,tspan,y0,opts)%增加收敛性，计算时间0.0214

toc

tic

sol=ode23tb(@ode7,tspan,y0,opts)%增加收敛性，计算时间0.0214

toc

%刚性求解器 ode23s,ode23t,ode23tb

function dy=ode7(x,y)

dy=zeros(2,1);

dy(1)=y(2);

dy(2)=1000*(1-y(1)^2)*y(2)-2*y(1);

end

%不能求解符号解，添加属性'implicit',true,隐式解析解

%若隐式求解仍不能，则使用数值解法

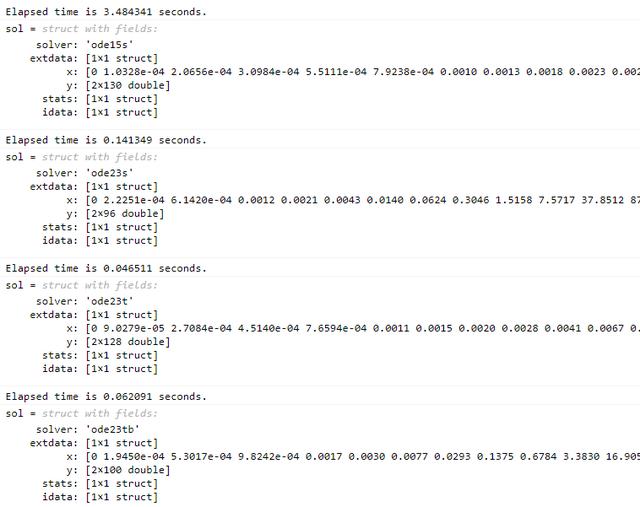
求解时间输出结果