52个立体几何综合训练（丰富的几何图形）

立体图形分类：柱体 （棱柱、圆柱）； 锥体（棱锥、圆锥）； 球

或：多面体（棱柱，棱锥），旋转体（圆柱、圆锥、球）

n棱柱： 2n个顶点，3n条棱，n 2个面。

n棱锥： n 1个顶点，2n条棱，n 1个面。

欧拉公式：多面体的 顶点数 面数-棱数=2

正方体展开折叠图：一四一型 二三一型 二二二型 三三型

口诀：一线不过四 田凹应弃之，间一“Z”端是对面 间二拐角邻面现。

截一个n面体：截面图形的边数不超过n。

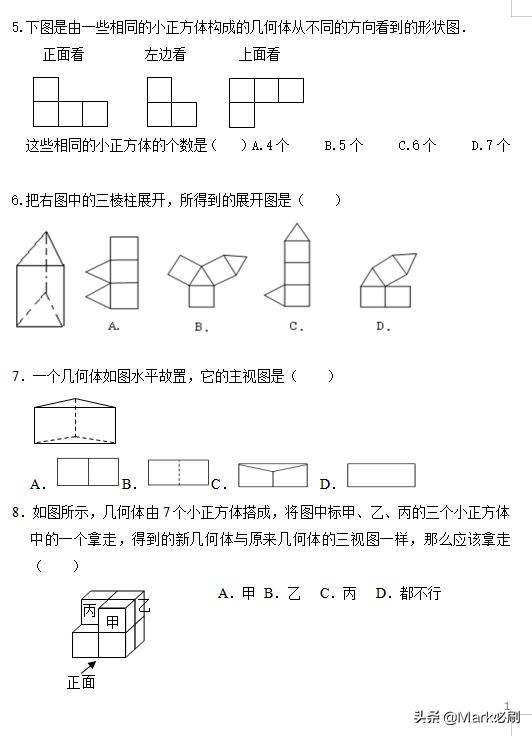
从三个方向看物体：左 正 上

熟练理解想象：三棱锥 三棱柱 四棱锥 四棱柱 圆锥 圆柱 的截面和视图。

会根据截面和视图 展开图 求面积和体积。

会通过视图确定小正方体堆积问题的个数。