样本量的计算公式名称（功效与样本量的计算）

我经常被问到这样的问题：“做假设检验时，需要的样本量是多少”， “我的实验究竟需要多少样本才有意义呢？”，这类问题可以通过功效与样本量计算来解决。

什么是功效？

所有检验都不可能尽善尽美，总存在这样的可能，即当原假设 (H0) 实际为真时您会根据检验结果否定原假设（I 型错误），或当原假设实际为假时您根据检验结果未能否定 H0（II 型错误）。这是因为为了估计总体均值，您必须使用随机样本，而这些随机样本都是随机抽取的。

第II类错误（被坑）的概率为β，而1- β我们称之为功效。II类错误是如果有个人有罪，而错误地判他无罪，所以“功效”就可以理解为，如果他实际上确实有罪，而且法官正确地判断他有罪的概率。

假设检验的功效受到检验的样本数量、差值、数据变异性和显著性水平的影响。

案例分析

一种镇定剂中的活性成分的目标含量为365mg/ml，每批镇静剂在使用前都要进行检测，以发现明显偏离目标的情况。

数据收集：从6个不同批次中随机抽取6个样品，测量其中的有效成分含量。

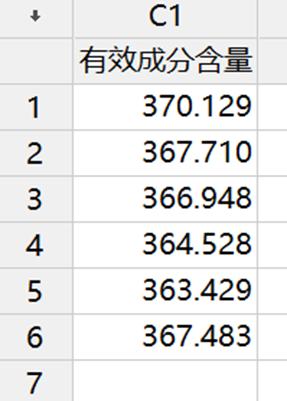
• 描述性统计分析

注意：不能直接从描述性统计量中得到偏离目标含量365mg/ml的结论，即使样本均值确实不是365mg/ml.

• 单样本t检验

单样本t检验的结果显示P＞0.05，故不拒绝原假设，换句话说，没有足够的证据拒绝有效成分含量均值为365mg/ml。

• 功效与样本量的计算

在这里，我不得不对上面的对话框做一些解释（我亲爱的客户朋友经常对此有疑问）。

差值

差值是在检测总体参数的假设值与实际值时您想得到的最小差值，看不懂，没关系，我们举个例子。在上面的对话框中我输入的差值为-2.5和2.5，为什么呢？因为在这里我认为，如果有效成分含量偏离目标值2.5mg/ml时，我就认为是有显著偏离，当然这里的偏离可以偏大（2.5），也可以偏小（-2.5）。

标准差

在功效和样本数量分析中使用的标准差取决于您是否已收集了数据。

1) 尚未收集数据：请使用总体标准差的估计值。您的估计值应以相关研究、设计规范、试验研究、学科知识或相似信息为基础。

2) 如果您已经收集并分析了数据，则使用下表所示的分析结果所提供的值。

Minitab结果如下：

结果显示，当样本量只有6个时，这时候的检验功效只有0.54，或者说犯第二类错误的概率高达0.46。功效太低，当前没有显著差异的结论很可能是样本量不足导致。

如果对于此分析，我想功效不低于0.9，那么这时候我该抽取多少样本量呢？

Minitab结果显示，要想功效不低于0.9，那么这时候我们需要再抽6个样本，一共12个样本才行。

• 再来一次单样本t检验

现在，又再抽了6个样本，一共12个样本，再来做一次假设检验。

这时候我们发现，当样本量增加到12时，P＜0.05，故拒绝原假设，得到有显著偏离目标值的结论。

• 小结

检验所需样本量的多少取决于你愿意承担多大犯错误的风险，所以，当你以后分析纠结样本量够不够时，请尝试先做个功效和样本量的计算。

如果检验的功效低，则您可能无法检测到效应并错误地得出不存在任何效应的结论。另外，也要注意如果检验的功效太高，则很小的效应或不需要关注的效应看上去都可能会很显著。

• 思考

如何提高假设检验的功效？