线性非晶态聚合物温度形变曲线（温度影响石墨烯）

黄立新 周昆 黄君 叶太智广西大学土木建筑工程学院 广西大学工程防灾与结构安全教育部重点实验室

摘 要：采用分子动力学模拟方法研究了温度对石墨烯/沥青复合材料界面微结构特征的影响。选取沥青的4组分模型，进行分子动力学模拟，得到合理的沥青玻璃化转换温度。然后加入石墨烯，共同搭建石墨烯/沥青复合材料模型并进行分子动力学模拟。在此基础上，基于复合材料切片的相对浓度，定义界面区间的范德华间隙和致密区间。根据复合材料相对浓度曲线，计算得到范德华间隙厚度，然后采用统计学方法，得到沥青基体累计浓度以及一阶导数的曲线，计算得到致密区间厚度。在各种温度条件下，通过分子动力学模拟得到石墨烯/沥青复合材料界面区间范德华间隙和致密区间的厚度。研究结果表明，温度对致密区间厚度影响较小，而对范德华间隙厚度影响较大；并且在玻璃化转换温度之前随着温度升高范德华间隙厚度波动下降，玻璃化转换温度之后随温度升高范德华间隙厚度逐步增大。

关键词：石墨烯改性沥青;分子动力学模拟;范德华间隙;致密区间;温度影响;

基金：国家自然科学基金项目，项目编号11262002;

沥青主要是来自原油蒸馏的副产物，是一种高度复杂的材料，包含105～106种不同的分子[1]。近年来，常加入纳米材料对沥青进行改性，以获得性能更优异、更稳定的沥青混合料[2,3]。沥青纳米复合材料在双材料界面是薄弱环节，界面微结构特征对复合材料力学性能、破坏强度都有显著影响[4]。因此界面微结构特征是研究复合材料力学性能的重点。

文献[5,6,7]分别采用扫描电镜、X射线、原子力显微镜对沥青复合材料微观界面进行直接观察，以得到复合材料界面破坏机制。其试验费时费力，并且微观上不便于了解沥青与其他成分的作用机制。分子动力学(Molecular Dynamics, 简称MD)模拟是研究这些微观作用机制的有效途径之一。Xu等[8]利用MD方法对沥青的密度、溶解度参数等物理性质进行预测，并通过对黏附功的构成进行分析，得出范德华(van der Waals, 简称vdW)力对沥青结合料的黏结性能起着关键作用的结论。Ramezani等[9]由MD模拟得出，在碳纳米管改性沥青界面中，vdW力作用对黏结性能做出了主要贡献。因此，vdW力作用对复合材料界面力学性能的影响显著。

沥青作为一种热敏感性材料，环境温度的变化会使沥青料面层处于非定常和非均匀的状态[10]。研究变温度下沥青的力学性能是当前的热点。Zhou等[11]通过试验测量了碳纳米管改性沥青和石墨烯改性沥青(Graphene Modified Asphalt, 简称GMA)的玻璃化转换温度等热力学性能，后与MD模拟结果对比，计算得到的温度值和试验结果吻合良好；模拟发现随着温度升高，改性沥青的杨氏模量、剪切模量会逐渐减小。Liu等[12]对沥青混合料不同温度下静态动态荷载作用的力学性能进行分析，结果表明温度的升高会使沥青力学性能下降。Ouyang等[13]建立数学模型描述不同温度下沥青的抗压强度和杨氏模量；但该方法由于模型使用温度范围内不能存在玻璃化转换温度而具有明显的局限性。Zhu等[14]研究了二氧化硅对改性沥青的热力学和力学性能方面的影响，结果表明改性沥青的玻璃化转换温度随着二氧化硅掺入量的增加而降低，且力学性能随着填料的增加而逐渐提升；但对于温度对力学性能影响的微观机制，文献并没有进一步说明。

综上所述，沥青复合材料的界面微结构特征对研究复合材料力学性能具有重要意义，而温度对界面微结构特征的影响研究甚少。本文选取沥青的4组分模型，将石墨烯作为增强材料加入沥青，采用软件Material Studio 2017(简称MS)进行分子动力学模拟，首先计算得到沥青的玻璃化转换温度并与试验值对比，然后通过切片方法得到石墨烯/沥青复合材料相对浓度曲线，求出vdW间隙厚度，最后采用统计学方法求得致密区间厚度，并研究了在不同温度下vdW间隙和致密区间的变化情况。

1 分子动力学模拟理论

MD模拟的基本方法是将模拟物质看作一个集合体，之后通过数值求解该集合体体系经典力学运动方程，并统计体系的结构特征与性质[15]。通常，统计体系有以下几种，包括微正则系综(NVE系综)、正则系综(NVT系综)、等温-等压系综(NPT系综)、等焓-等压系综(NPH系综)和广义系综[16]。本文采用的NVT系综是指粒子数N、体积V、温度T都相同的热力学体系，晶胞内温度恒定，总能量发生变化。NPT系综内部体系压力恒定，但体积会发生改变，模拟中常用于压缩晶胞体积以达到真实材料的密度。

在GMA的动力学模拟中，采用凝聚相分子势能优化力场(Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies, 简称COMPASS)。该力场用于描述键合相互作用和非键合相互作用，对于聚合物、无机小分子和大多数有机物，已被验证能够非常精确地拟合试验数据[17]。力场可表达为：

Ebonded=Eb Eθ Et Eo Eb,b′ Eb,θ Eθ,θ′ Eb,t Eθ,t Eθ,t,θ′ (1)

Enon-bonded=EvdW Ecoul (2)

Etotal=Ebonded Enon-bonded (3)

式中：Eb为键伸缩势；Eθ为键角弯曲势；Et为二面角扭曲势；Eo为离面弯曲势能；交叉耦合项包括伸缩-伸缩耦合势Eb,b′、伸缩-弯曲耦合势Eb,θ、弯曲-弯曲耦合势Eθ,θ′、伸缩-扭转耦合势Eb,t、弯曲-扭曲耦合势Eθ,t、弯曲-扭曲-弯曲耦合势Eθ,t,θ′;非键合相互作用包括vdW相互作用势EvdW、静电相互作用势Ecoul。

模型搭建使用Amorphous Cell(简称AC),基于MD的Forcite模块进行操作计算。vdW相互作用采用基于原子的求和法，静电相互作用采用Ewald求和法，截断半径取1.55 nm。除GMA模型弛豫外，其余过程均选用Nose恒温器和Berendsen恒压器分别用于维持目标温度和压力。所有的模拟都是在1 fs的时间步长、1个大气压的压力下进行的。

2 模型建立2.1沥青模型建立

美国战略公路研究计划(SHRP)根据溶解度将沥青分为了沥青质、极性芳香烃、环烷芳香烃、饱和烃等4种组分[18,19]。Derek等[20]在此基础上提出4组分模型。本文选取该模型是因为其能很好地模拟真实情况下的沥青，而且它们的分子量和分子面积基本相同，便于计算。模型每个单独的分子结构如图1所示，模型采用相关参数见表1。

图1 沥青4组分模型分子结构 下载原图

表1 沥青4组分模型参数 导出到EXCEL

组分	分子名称	化学式	分子量g/mol分子量g/mol	分子个数个分子个数个
沥青质	Asphaltene-phenol	C42H54O	574.89	3
	Asphaltene-pyrrole	C66H81N	888.38	2
	Asphaltene-thiophene	C51H62S	707.11	3
饱和烃	Squalane	C30H62	422.82	4
	Hophane	C35H62	482.88	4
环烷芳香烃	PHPN	C35H44	464.73	11
	DOCHN	C30H46	406.69	13
极性芳香烃	Quinolinohopane	C40H59N	553.91	4
	Thioisorenieratane	C40H60S	572.97	4
	Trimethylbenzeneoxane	C29H50	414.71	5
	Pyridinohopane	C36H57N	503.85	4
	Benzobisbenzothiophene	C18H10S2	290.39	15

在选取了沥青组分以后，需要建立沥青晶胞，具体步骤如下。

(1)在MS中建立好沥青的12个分子，然后分别对每个分子进行几何优化和能量最小化。

(2)构建沥青分子的AC模型。为防止分子链相互缠绕，必须使上述分子分布完全随机，并在AC模块以0.1 g/cm3的初始密度进行沥青三维周期模型的构建。建立好的沥青初始晶胞尺寸为8.05 nm×8.05 nm×8.05 nm。然后对该晶胞再进行一次几何优化，迭代次数取10 000次，精度取最高。

(3)沥青分子AC模型的退火(Annealing)操作。由于AC模块采用的是蒙特卡洛法，所有分子是完全随机分布的，所以由此搭成的模型能量极高，不利于后续计算，要对其进行退火操作。退火时，温度区间取300 K～800 K,精度取最高，进行50次迭代，并在迭代过程中再次进行分子优化。完成后在这50个构型中选取能量最低的一帧进行后续操作。

(4)经过退火操作后，为了让沥青体系在目标温度下从初始状态进入更为平衡的状态，实现体系的预平衡，模型进行500 ps的NVT系综弛豫，之后再进行500 ps的NPT系综弛豫。弛豫过程如图2所示。随着时间增加，沥青三维周期模型晶胞尺寸减小，密度逐步上升至真实密度。在温度T为298 K、1个大气压下(p=1 atm),弛豫后的沥青模型如图3所示。弛豫后尺寸为3.752 nm×3.752 nm×3.752 nm, 密度稳定在0.99g/cm3,与SHRP试验[19]所测得的1.03 g/cm3相差不大，结果理想。

图2 NPT弛豫下的密度变化 下载原图

2.2石墨烯模型的建立

在建立石墨烯模型时，取用MS中自带的周期性石墨烯三维模型。由于在后续操作中进行复合材料界面搭建模型时，石墨烯片晶胞尺寸需同沥青模型晶胞尺寸相近，才能够进行搭建，故需要在单个石墨烯的基础上建立超晶胞。石墨烯超晶胞平面尺寸为3.935 nm×3.834 nm, 如图4所示。

图3 沥青晶胞模型 下载原图

图4 石墨烯超晶胞模型 下载原图

2.3复合材料模型的建立

界面搭建时，为了使石墨烯在系综弛豫后仍在晶胞范围内，研究中放置两片石墨烯加以稳定。为防止底层石墨烯对沥青产生影响，导致结果错误，需对底层石墨烯坐标进行固定。搭建好界面模型后，需要对界面搭建模型进行几何优化、NVT系综弛豫，使能量预稳定。最后进行500 ps的NPT系综弛豫，恒温器选择Nose, 恒压器选择Souza-Martins, 将y方向压力设置为1个大气压(p=1 atm),其余方向全部设置为0。平衡后的晶胞如图5所示。

3 结果与分析3.1沥青玻璃化转换温度

沥青作为一种无定形物质，其分散体中存在大量胶体，致使存在一种特殊的温度，即玻璃化转换温度Tg。玻璃化温度Tg对沥青力学性能的影响很大。低于该温度之时沥青处于玻璃态，其本构关系为线性；而在高于该温度之时沥青处于高弹态，表现出黏弹性体的性质。对于沥青这样一种物理性质随温度变化的材料，需要对其玻璃化转换温度进行分析。

图5 石墨烯改性沥青模型 下载原图

在MS中编写脚本计算沥青模型的玻璃化转换温度Tg,温度区间取在188.15 K～368.15 K之间，以20 K为温度间隔进行计算，模拟得到10个温度下对应的沥青密度，结果见表2。根据表2数据画出沥青温度～密度散点图，如图6所示。从图6中可以看出，沥青密度随温度的升高而降低，并且温度～密度曲线的斜率有明显变化的区间。玻璃化转换温度可以理解为温度～密度曲线上两条线性回归线相交点的温度。因此首先目测数据点，粗略估计出两条回归线相交位置。然后以该位置作为分界，将数据点分为左右两个部分，即分为188 K～248 K和268 K～368 K两个区间。分别用最小二乘法对两部分数据点进行回归分析，得到两条回归直线方程，即：

D=-9.5×10-5T 1.047 (188≤T≤248) (4)

D=-4.7×10-4T 1.146 (268≤T≤368) (5)

式中：T表示温度；D表示密度。

表2 不同温度下的沥青密度 导出到EXCEL

温度/K	188.15	208.15	228.15	248.15	268.15	288.15	308.15	328.15	348.15	368.15
密度/(g·cm-3)	1.028	1.028	1.027	1.022	1.018	1.011	1.002	0.993	0.984	0.970

图6 沥青温度～密度散点分布 下载原图

联立求解方程可以得到交点为(263.76,1.021 9),故沥青玻璃化转换温度Tg为263.76 K。

本文得到的沥青玻璃化温度与文献结果的比较列于表3。可以看出测量方法不同，各文献所得Tg差别较大。但由于Tg属于一个温度范围，故本文所得结果Tg=263.76 K是合理的，证明所采用的模型可以进行下一步的模拟计算。

表3 沥青玻璃化温度结果比较 导出到EXCEL

本文结果		文献结果
方法	Tg/K	方法	Tg/K
分子动力学	263.76	试验[21]	248.55
		分子动力学[22]	298.15
		试验[23]	223～303
		分子动力学[11]	250
		分子动力学[14]	278.66

3.2范德华间隙与致密区间

vdW间隙是石墨烯与沥青基体材料之间存在的由vdW力和静电力共同作用产生的真空带。随着作用距离的增加，vdW作用力会产生吸引势，作用于沥青基体，导致作用区域内密度增加。该作用区域即为致密区间。由于所用系统属于微观层面，故采用相对浓度对复合材料界面区间性质进行讨论更为精确。首先将晶胞等分为N个盒子，则相对浓度表达式为：

cR=cic¯ (0<i≤N)         (6)cR=cic¯ (0<i≤Ν)         (6)

式中：cR为相对浓度(Relative Concentration);ci为第i个盒子内原子浓度；c¯c¯为晶胞内原子的平均浓度。

ci和c¯c¯分别由下式计算：

ci=niVi (0<i≤N)         (7)ci=niVi (0<i≤Ν)         (7)

c¯=ntotalVtotal         (8)c¯=ntotalVtotal         (8)

式中：ni为第i个盒子内原子总数；Vi为第i个盒子体积；ntotal为晶胞内原子总数；Vtotal为晶胞体积。

现以1个大气压(p= 101 325 Pa)下、温度为208.15 K时的石墨烯/沥青复合材料分子动力学模型为例，对相对浓度计算进行说明。作图7所示的坐标系，模型几何尺寸为3.857 nm×4.539 nm×3.766 nm。沿y轴方向将模型等分为300个盒子，每个盒子厚度为0.015 13 nm。随着y轴坐标增大，由小到大进行盒子的编号。根据公式(6)～公式(8)计算得到每个盒子原子相对浓度，进而得出复合材料相对浓度曲线，如图8所示。在图8中，曲线在A点(yA=0.624 nm)前出现的两个波峰为石墨烯片，从B点(yB=0.749 nm)开始沥青浓度上升，A、B点距离即为vdW间隙厚度。由于石墨烯对基体的吸引力较大，使得沥青浓度陡增，出现第三个波峰C点(yC=0.848 nm),然后波动变化趋于平稳。平稳开始的D点为致密区间结束点。

图7 等分示意 下载原图

为了确定致密区间厚度，需求出致密区间末端D点坐标，因此单独分析沥青基体浓度随y坐标的变化情况。选择图8复合材料浓度曲线中的基体部分进行放大，如图9(a)所示。得到的放大曲线波动幅度过大，采用目测法不利于精确处理致密区间。为了减少波动，本研究参照统计学方法[24],对其修正后进行沥青基体浓度曲线的处理。首先进行平均累积浓度处理，计算公式为：

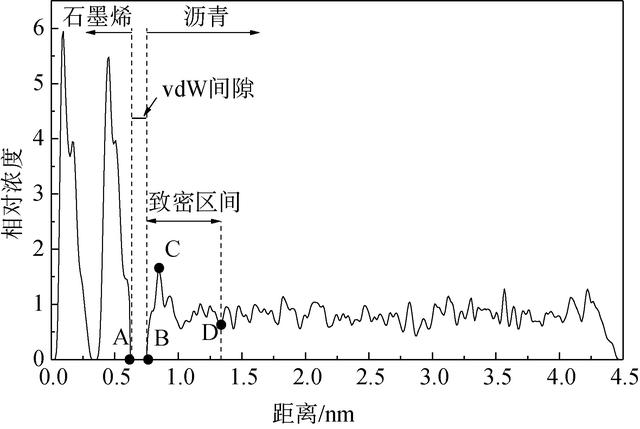
图8 复合材料浓度曲线 下载原图

ca(s)=1N1∑i=bscica(s)=1Ν1∑i=bsci(b<s) (9)

式中：ci为第i个盒子的浓度；b为B点处的盒子编号；s为B点外某点处的盒子编号；N1是统计样本[b,s]中的盒子总数，表示统计样本上限。

图9 沥青相对浓度和累积浓度 下载原图

经过处理后得到累计浓度曲线，如图9(b)所示。可以观察到图9(b)中沥青累计浓度曲线仍然有较大幅度波动，依旧不便于确定D点坐标。因此在累积浓度的基础上，引入标准差函数可以更好地观察其曲线变化情况。累积标准差(Accumulated Standard Deviation, 简称为ASD)定义为：

ASD(s)=1N1∑i=bs(ci−c¯ave)2−−−−−−−−−−−−−−−√         (10)ASD(s)=1Ν1∑i=bs(ci-c¯ave)2         (10)

式中：c¯avec¯ave为基体浓度的平均值，表达式如式(11)所示。

c¯ave=∑i=b300ci300−b 1         (11)c¯ave=∑i=b300ci300-b 1         (11)

对ASD曲线求一阶导数，即d(ASD)dyd(ASD)dy。图10是ASD及其一阶导数的曲线图。由图10可知，沥青基体ASD曲线先迅速减小，而后趋于平稳。但通过ASD曲线不易看出开始趋于平缓的点的位置，而在d(ASD)dyd(ASD)dy曲线上，取曲线斜率为0的点为致密区间结束点D。

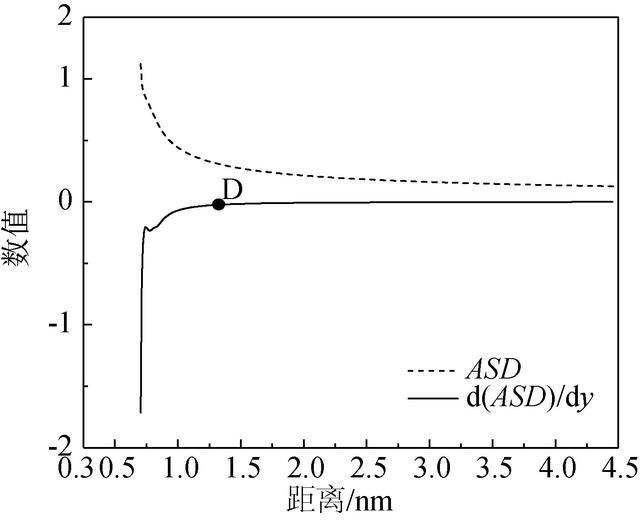
图10 累积标准差及其一阶导数 下载原图

由图7可以看出，vdW间隙厚度tvdW及致密区间厚度tDense分别为：

tvdW=yB−yAtDense=yD−yB         (12)tvdW=yB-yAtDense=yD-yB         (12)

式中：yA、yB、yD分别为A、B、D点的纵坐标值。

采用相同的方法分析208.15 K～328.15 K之间9个不同温度的vdW间隙以及致密区间厚度，所得结果见表4。由表4可知，在9个不同温度情况下，tDense稳定在0.6 nm上下。在T=208.15 K和T=238.15 K即温度较低时，vdW间隙厚度基本不发生改变，因为此时温度较低的沥青分子间结构以及空间位置处于极为稳定的状态。当温度T慢慢升高到玻璃化转换温度263.76 K的过程中，tvdW会逐渐减小，并在玻璃化转换温度(T=263.76 K)的时候达到最小值0.090 nm; 而后随温度升高tvdW逐步增大，并在温度T=328.15 K时，tvdW达到最大值，为0.198 nm。综上所述，温度的变化对致密区间影响较小，而对vdW间隙厚度影响较大，并且vdW间隙厚度在玻璃化转换温度Tg处得到最小状态；温度高于玻璃化转换温度Tg之后，vdW间隙厚度随温度增高而变大。

表4 不同温度下的界面参数 导出到EXCEL

温度/K	yA/nm	yB/nm	yD/nm	tvdW/nm	tDense/nm
208.15	0.624	0.749	1.341	0.125	0.592
238.15	0.606	0.732	1.334	0.126	0.602
253.15	0.579	0.687	1.317	0.108	0.575
263.76	0.579	0.669	1.361	0.090	0.692
268.15	0.580	0.696	1.343	0.116	0.647
283.15	0.580	0.733	1.335	0.153	0.602
298.15	0.580	0.741	1.298	0.161	0.557
313.15	0.580	0.732	1.370	0.152	0.638
328.15	0.553	0.751	1.345	0.198	0.593

4 结语

(1)选取沥青的4组分模型，采用Material Studio 2017软件进行分子动力学模拟，得到在298 K和1个大气压下沥青的密度为0.99 g/cm3,与文献的试验值1.03 g/cm3比较吻合。

(2)在188.15 K～368.15 K的温度区间，以20 K为温度间隔进行分子动力学模拟计算，得到10个温度下对应的沥青密度。然后采用线性回归方法，得到沥青的玻璃化转换温度为263.76 K。与文献的结果对比发现，该玻璃化转换温度在合理范围之内。

(3)在沥青模型中加入石墨烯，共同搭建复合材料模型并进行分子动力学模拟，结果表明界面区间不仅存在范德华间隙，而且由于范德华力和静电力的作用使得沥青基体存在致密区间。

(4)各种温度条件下，通过分子动力学模拟计算得到石墨烯/沥青复合材料界面区间范德华间隙和致密区间的厚度。研究结果表明，温度对致密区间厚度影响较小，而对范德华间隙厚度影响较大。在玻璃化转换温度之前，随着温度升高范德华间隙厚度波动下降；在玻璃化转换温度之后，随着温度升高范德华间隙厚度大体上逐步增大。并且在玻璃化转换温度之前温度较低时(T=208.15 K和T=238.15 K),范德华间隙厚度基本不变，界面区间处于稳定状态，界面区间厚度基本不发生改变；而在玻璃化转换温度之后，温度升高会使界面区间的范德华间隙厚度发生较为明显的增大，导致界面区间厚度也增大。因此在石墨烯/沥青复合材料的力学性能研究中，需要考虑温度的影响。

参考文献

[1] Wiehe I A,Liang K S.Asphaltenes,resins,and other petroleum macromolecules [J].Fluid Phase Equilibria,1996,117(1996):201-210.

[2] 张起森，肖鑫.沥青及沥青混合料本构模型与微观结构研究综述 [J].中国公路学报，2016,29(5):26-33.

[3] Du H,Pang S D.Enhancement of barrier properties of cement mortar with graphene nanoplatelet [J].Cement and Concrete Research,2015,76(2015):10-19.

[4] Zhu X Y,Yang Z X,et al.Modulus prediction of asphalt concrete with imperfect bonding between aggregate-asphalt mastic [J].Composites Part B:Engineering,2011,42(6):1404-1411.

[5] Poulikakos L D,Partl M N.Investigation of porous asphalt microstructure using optical and electron microscopy [J].J Microsc,2010,240(2):145-154.

[6] Bhasin A,Izadi A,BEDGAKER S.Three dimensional distribution of the mastic in asphalt composites [J].Construction and Building Materials,2011,25(10):4079-4087.

[7] Dong Z,Liu Z,et al.Nanostructure characterization of asphalt-aggregate interface through molecular dynamics simulation and atomic force microscopy [J].Fuel,2017,189:155-163.

[8] Xu G,Wang H.Molecular dynamics study of interfacial mechanical behavior between asphalt binder and mineral aggregate [J].Construction and Building Materials,2016,121:246-254.

[9] Ramezani M G,Rickgauer J.Understanding the adhesion properties of carbon nanotube,asphalt binder,and mineral aggregates at the nanoscale:a molecular dynamics study [J].Petroleum Science and Technology,2019,38(1):28-35.

[10] 郑健龙，钱国平，应荣华.沥青混合料热粘弹性本构关系试验测定及其力学应用 [J].工程力学，2008,25(1):34-41.

[11] Zhou X,Zhang X,et al.Evaluation of thermo-mechanical properties of graphene/carbon-nanotubes modified asphalt with molecular simulation [J].Molecular Simulation,2017,43(4):312-319.

[12] Yongliang L,Xiangming K,et al.Static and Dynamic Mechanical Properties of Cement-Asphalt Composites [J].Journal of Materials in Civil Engineering,2013,25(10):1489-1497.

[13] Ouyang J,Zhao J,Tan Y.Modeling Mechanical Properties of Cement Asphalt Emulsion Mortar with Different Asphalt to Cement Ratios and Temperatures [J].Journal of Materials in Civil Engineering,2018,30(10):1-10.

[14] Zhu X,Du Z,et al.Effect of filler on thermodynamic and mechanical behaviour of asphalt mastic:a MD simulation study [J].International Journal of Pavement Engineering,2018,21(10):1248-1262.

[15] 严六明，朱素华.分子动力学模拟的理论与实践 [M].北京：科学出版社，2013:1-6.

[16] Bandyopadhyay A,Valavala P K,et al.Molecular modeling of crosslinked epoxy polymers:The effect of crosslink density on thermomechanical properties [J].Polymer,2011,52(11):2445-2452.

[17] Sun H.COMPASS:An ab Initio Force-Field Optimized for Condensed-Phase Applications Overview with Details on Alkane and Benzene Compounds [J].The Journal of Physical Chemistry B,1998,102:7338-7364.

[18] Robertson Re B J.Fundamental Properties of Asphalts and Modified Asphalts,Volume 1 Interpretive Report [M].Federal Highway Administration.2001.

[19] Jones D R.SHRP Materials Reference Libary:Asphalt Cements:A Concise Data Compilation [M]//Council Strategic Highway Research Program National Research.National Research Council,Washington,DC.1993.

[20] Li D D,Greenfield M L.Chemical compositions of improved model asphalt systems for molecular simulations [J].Fuel,2014,115(1):347-356.

[21] Broome D C.Asphalt:Science and Technology [J].Nature,1964,202(4934):739-740.

[22] Zhang L,Greenfield M L.Analyzing Properties of Model Asphalts Using Molecular Simulation [J].Energy & Fuels,2007,21(3):1712-1716.

[23] Tabatabaee H A,Velasquez R,Bahia H U.Predicting low temperature physical hardening in asphalt binders [J].Construction and Building Materials,2012,34:162-169.

[24] Alizadeh Sahraei A,Mokarizadeh A H,et al.Insights into interphase thickness characterization for graphene/epoxy nanocomposites:a molecular dynamics simulation [J].Phys Chem Chem Phys,2019,21(36):19890-19903.

声明：我们尊重原创，也注重分享。有部分内容来自互联网，版权归原作者所有，仅供学习参考之用，禁止用于商业用途，如无意中侵犯了哪个媒体、公司、企业或个人等的知识产权，请联系删除，另本头条号推送内容仅代表作者观点，与头条号运营方无关，内容真伪请读者自行鉴别，本头条号不承担任何责任。

,