每日五题物理（物理每日一题）

如图，质量为m＝1Kg的小滑块（视为质点）在半径为R的四分之一光滑圆弧的最高点A，由静止开始释放，它运动到B点时速度为2m/s。当滑块经过B后立即将圆弧轨道撤去。滑块在光滑水平面上运动一段距离后，通过换向轨道由C点过渡到倾角＝37°，长L＝1m的斜面CD上，CD间铺了一层特殊材料，其动摩擦因数取值范围为0≤μ≤1.5，斜面底部D点与光滑地面平滑相连，地面上一根轻质弹簧一端固定在O点，自然状态下另一端恰好在D点，认为滑块在C，D两处换向时速度大小均不变，最大静摩擦等于滑动摩擦。（空气阻力不计，g取10m/s^2）

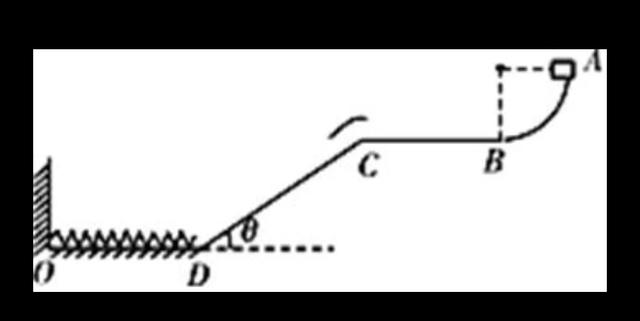
问：(1)求光滑圆弧的半径R以及滑块经过B点时对圆弧的压力大小。

(2)若μ＝0，求滑块从C第一次运动到D的时间及弹簧的最大弹性势能。

(3)若滑块最终停在D点，求μ的取值范围。

这题一眼看过去题目很长，开头的一句“撤去圆弧轨道”似乎也莫名其妙，但这时不要着急，慢慢分析下去就知道它有什么用，我们开始分析。（注：下面分析中VB2就是说B点速度的平方，其它字母同理）

解：(1) 第一问我们对物块分析，由于圆轨道光滑，所以物块从A到B无能量损耗，因此减少的重力势能完全转化为B点的动能，有mgR＝mVB2/2 得R＝0.2m

然后对物块在B点进行受力分析，它在B点只受到两个力，一个是竖直向上的弹力N，另一个是竖直向下的重力mg，这两个力的合力提供向心力，因此有N－mg＝Fa＝mVB2/R，解得N＝30N。但注意这里还没有答完，题目问的是物块对圆轨道的压力大小，而你这里的受力分析是分析了圆轨道对物块的弹力大小，因此你需要再说一嘴，根据牛顿第三定理，N与F压大小相等，所以F压＝30N。

(2) 第二问给出条件μ＝0，因此我们会发现物块在整个运动过程中没有任何内能产生，物块在C点速度Vc＝2m/s，对斜面上的物块再做受力分析，把重力沿着斜面方向分解，可知物体仅受到沿斜面向下的6N下滑力以及斜面给的8N支持力。但由于μ＝0，因此8N支持力在此题中用不上，我们只考虑6N的下滑力，很明显这就是物体的合外力。

由F合＝ma，可知物体在斜面上做a＝6m/s2的匀加速直线运动，有VD2－VC2＝2aL，得VD＝4m/s，因此△V等于VD－VC＝2m/s，再由a的定义式a＝△V/△t，求出△t＝1/3秒

物体在OD段时，仅有动能与弹簧的弹性势能相互转化，因此当物体的动能完全转化为弹簧的弹性势能时，EP达到最大值，有EP（max）＝EDK＝mVD2/2＝8J

(3) 从题目我们可以看出，弹簧的作用其实就是把物块顶回斜面，换而言之你可以理解为弹簧的作用就是让物体在D点的速度反向，它本身不损耗物块能量（因为一定会还回去），而整个装置仅有斜面CD粗糙，因此物块所有的能量损耗都只能由斜面来承担。

我们假设μ从0开始逐渐增大，当μ非常小时，由于物体在C处本身有动能，因此若斜面消耗的能量过少，则物块有可能冲回C点，到这里你就发现题干中“撤去圆轨道”有什么作用了，这就是告诉你物块回到C点就会从B点掉下去，因此让物块能回到C点的所有μ都是不可取的，我们只需要算出让物块恰好回到C点的临界μ就可以了。由于物块前后都在C点，因此重力没有做功，有mVC2/2＝Wf＝2Lf＝16μ，解得μ等于1/8，可见0≤μ＜1/8是不可取的区间。

然后μ继续增大，这时物块一定不可能回到C点了，它只能滑到斜面上，那么下一个临界是什么呢？其实就是物块恰好能自由静止在斜面上的那个μ。若物块不能静止在斜面上，那么它只能掉到弹簧上，而弹簧必定把它再顶回斜面，这时你发现物块在弹簧与斜面处都停不住，那它只有1个地方可以停了，那就是我们要求的D点。此时物块会在OD段与CD段来回运动，且由于CD的摩擦力消耗使得其运动幅度不断减小，最终能量耗尽而停在D点。对于临界分析有sin37mg＝cos37mgμ，得μ＝tan37＝3/4。因此我们发现1/8≤μ＜3/4可取。

然后μ继续增大，此时物块可以静止在斜面上，而它的能量显然不足以支撑它经过斜面2次，因此它若要停在D点只能一次就恰好滑到D点停住。有Wf＝16μ＝mVC2/2＋mgsin37L， 解得μ＝1。因此当3/4≤μ≤1.5时，仅有μ＝1可取。

综上，μ的取值范围为1/8≤μ＜3/4或μ＝1