高铁的可行性研究报告 基于数学模型分析高铁建设对出行选择的影响

作者：郑铿城，经济学博士，数学建模指导教练

文章摘要

随着近几年我国经济的飞速发展与科技水平的不断提高，人们的出行越发的便捷，于此直接带来交通拥堵等的问题，因此对交通方式的研究和优化迫在眉睫。本文采用AHP、熵值定权法、模糊物元法对高速公路通行压力进行评价，并采用逐步回归法探究与高铁之间的内在联系，并对显著性进行检验，之后采用多元回归模型与Verhulst对上海、青岛、乌鲁木齐最优高铁配置数量进行计算。

针对问题一：首先选择交通管理水平、信息服务水平以及安全水平，并选取铁路客运量、铁路正式营业里程等9个可观测变量作为高铁对出行选择方式的相关指标，选取交通流量、高速公路饱和度等5个指标作为高速公路交通压力的评判指标。采用AHP与熵值定权法结合的最优赋权模型计算高速公路通行压力各指标的权重，并采用模糊物元法进行综合评价。可以看出2015年之前通行压力得分较为稳定，而之后的几年中急剧上涨。最后采用逐步回归模型建立高铁各指标与高速公路通行压力综合得分之间的联系，得到：R2=0.999，模型拟合优度高，且F=8867.81,p=0.0082127，p<0.05，模型通过检验，且显著性水平很高，同时各自变量均对被解释变量起到很好的解释效果。

针对问题二：选取上海、青岛、乌鲁木齐作为研究对象，选取选取人口总数（万人）、人口流动数（万人）、人均GDP（万元）、从事高铁行业的人员（万人）作为自变量，以高铁数目（对）作为因变量。为了防止为了减少异方差的影响，同时数据的自然对数不改变时间序列的性质和相互关系，并使其趋势线性化，因此对各个变量取对数的形式，建立多元回归模型，采用Matlab对数据进行拟合得到上海、青岛、乌鲁木齐模型分别为：

最后建立Verhulst模型，对各变量进行预测，最终得到2019年上海、青岛、乌鲁木齐最优配置数分别为：64.1627、21.8995、28.7231。

关键词：AHP；熵值法；最优赋权模型；模糊物元法；逐步回归模型；Verhulst模型；

一、问题重述

1.1 问题背景

随着近几年我国经济的飞速发展，全民幸福指数上升，许多家庭在节假日选择短途或者长途的自驾游，这就造成了高速公路的严重拥堵。与此同时，伴随着我国现代伟大发明之一的“高铁”出现，“四横四纵”铁路网完美收官，不仅大大压缩了通行的时间成本，同时也串起了一条条黄金旅游线路，对人口流动以及旅游业都产生了极大影响。远途出行的人们更倾向于高铁作为出行工具，对高速公路以及其他列车的交通压力有一定的缓解作用。

1.2 问题提出

问题一：高铁的开通，一部分人们便会选择高铁出行，从而会使得高速公路的车辆有所减少，请你选取合适的指标，分析高铁的开通对该高速公路的车辆通行压力是否有所减缓，并分析是否显著。

问题二：高铁即快捷，又舒适，但是相对于普通列车出行价格相对昂贵，因此不同地域的人出行方式的选择将会有所差异，请你选择发展不同的城市，尝试给出你所选城市高铁配置的最佳数量。

二、问题分析

针对问题一：首先需要选取指标并进行数据预处理，本文充分考虑高铁影响人们对于交通出行选择的各个因素，划分为3个部分，即：交通管理水平、信息服务水平以及安全水平，并选取铁路客运量、铁路正式营业里程等9个可观测变量作为高铁对出行选择方式的相关指标，选取交通流量、高速公路饱和度等5个指标作为高速公路交通压力的评判指标，指标体系如下：

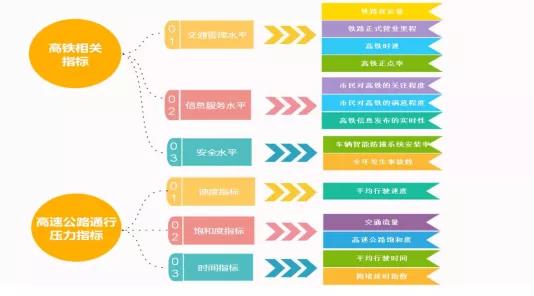
同时需要对数据进行预处理，即对缺失数据进行填补，本文采用三次样条插值算法对缺失数据进行填补，以降低与实际值的误差。首先需要建立合理的评估模型对高速公路交通情况进行准确的刻画，本文采用AHP模型与熵值定权法结合的最优赋权法对权重进行计算，采用模糊物元法建立综合评估模型。并采用逐步回归模型对变量进行剔除，以保证各个变量均显著，对评估结果进行回归，并做出相关分析。

针对问题二：需要选择不同城市计算其最优高铁配置数量，由于不同城市的GDP，人口数量等等条件均不同，因此需要对高铁配置数量与能够影响其因素进行研究分析，本文选取了人口总数（万人）、人口流动数（万人）、人均GDP（万元）、从事高铁行业的人员（万人）作为影响高铁配置数量因素，探究其对于高铁配置数量的影响，进而对最优配置数量进行计算。

三、模型假设

假设所查阅的相关数据真实可信，假设所选指标能够代表所要研究对象的整体情况，假设变量间的相关性不会对回归造成影响，假设对于给定点的数据集，三次样条插值填补缺失数据满足样条相互连接且两次连续可导。

四、符号说明

五、模型建立及求解

5.1 问题一模型的建立及求解：

5.1.1 指标的选择及数据的预处理：

5.1.1.1 指标选取：

5.1.2 高速公路流畅程度评估模型的构建及其求解：

首先构造综合评价模型对各年高速公路通行压力进行综合评判，本文采用熵值法结合AHP构造最优赋权模型，并采用模糊物元法对交通压力进行综合评价。

5.1.2.1 AHP定权模型构建：

首先需根据九级表度表构造判断矩阵：

5.1.3 回归模型的构建及其求解：

为建立更为准确客观的模型，首先需要对各指标相关性进行计算，防止高度相关导致多重共线性的问题，利用Matlab 2016a计算9个指标的相关系数并作图得到：

由于自变量个数较多，从上图可以很明显的看出自变量存在较强的相关性，为防止自变量较强的相关性所带来回归的多重共线性的问题，同时保证变量的显著性，即对因变量有较好的解释性，因此本文采用逐步回归法建立模型，逐步回归的基本思想[5]是将变量逐个引入模型，每引入一个解释变量都进行F检验，同时对已经选入的解释变量逐个进行t检验，当原来引入的解释变量由于后面解释变量的引入变得不再显著时，则将其删除。以确保每次引入新的变量之前回归方程中只包含显著性变量。不断重复上述过程，直到既没有显著的解释变量选入回归方程，也没有不显著的解释变量从回归方程中剔除为止。以保证最后所得到的解释变量集是最优的。同时由于铁路客运量（人）数量级较大，为了减少异方差的影响，同时数据的自然对数不改变时间序列的性质和相互关系，并使其趋势线性化，因此需要对其取对数的形式。

采用Matlab的stepwise工具箱建立模型：

5.2 问题二的分析与建模

高铁的建设，使人们的出行更加的方便快捷，但是高铁车票相对于其他车票而言更加的昂贵，不同地域人们的出行方式将会有所不同，通过选取“上海”，“青岛”和“乌鲁木齐”三座城市作为研究对象，研究分析在经济发展不同的城市中，高铁应该配置何种数量，才可以达到一个最佳情况。

5.2.1 数据收集和分析

通过对“上海”，“青岛”和“乌鲁木齐”三座城市的人均可支配收入情况、人口流动情况，各地居民用于交通出行的费用情况以及各地居民中从事高铁建设行业的人员数量进行数据统计和处理。

首先对三个省市三年内的人均可支配收入进行分析，得到下图：

通过上图可以看出，上海市的人均可支配收入最大，其次是山东省，最后是新疆省，人均可支配收入在一定程度上会影响到居民对于高铁的购买，在人均可支配收较大的城市，原则上应该配置更多的高铁数目。再通过对各地居民支出中，用于交通费用支出的数据进行统计分析：

在上图中，颜色越深的区域，表明该地的交通费用支出越多，明显在可以看出交通费用支出的大小关系：上海>山东>新疆。表明在选取的三个省市中，上海居民用于交通的消费支出占比较高，说明该地居民有可能更多的去购买高铁车票进行出行。再通过对三个省市就业人口中，从事高铁相关行业就业人员的数量进行统计和分析，做出下图：

分析可得，上海地区就业人员中，从事高铁相关行业的人员占比高于山东和新疆，新疆地区的高铁相关就业人员相对比重较小，高铁相关就业人员从事比重越大，说明这个城市在将来会有更大的高铁需求，所以在未来将会在该城市建设更多的高铁，满足需求。从人口流动情况进行分析，上海作为国际都市，每年都吸引很多人前来就业、读书、旅游等，人口流动较为频繁，同时，上海与过个城市有着贸易往来，所以在 发展的城市，高铁的建设有利于该地区的经济发展，同时山东作为人口大省，人们的出行选择会多样化，而新疆在我国西部，西部大开发将带动新疆的发展，在新疆建设高铁成本相对会比较大，所以在新疆配置合理的高铁数量，不仅可以减少大量的成本开支，也有利于带动新疆的发展，故选择这三个城市进行问题的研究具有一定的代表性。

六、模型灵敏度检验及评价

6．1灵敏度检验

对问题一回归模型进行灵敏度检验，根据文献[7]通常在回归计算中，由于资料和计算上的误差，使得结果会产生一定的误差，通常采用采用最小二乘法来估计回归模型中的参数，使得目标函数即误差达到最小，本文以引入离群值来观察拟合优度即R2的变化。多次改变原始自变量数据，最后拟合优度改变微小，模型灵敏度较好。

6.2模型评价

6.2.1模型优点

1、采用层次分析法结合熵值法构造的最优赋权模型，既降低了层次分析法的主观性，又弥补了熵值法的局限性。

2、采用模糊物元法建立高速公路通常情况的综合评估模型，并进行综合评价，避免了简单评估所带来不准确性的问题。

3、采用逐步回归法对各因子进行回归，对变量进行剔除，保证了各变量均为显著（p<0.05）即各自变量均对结果具有良好的解释性，模型拟合度极高（回归方程拟合优度R2达到了0.9999），模型拟合度极高，且模型整体显著性很好。

4、建立Verhulst预测模型，对数据少量且呈增长型数据类型具有很好的预测结果。

6.2.2模型缺点

数据较难以查询，缺失数据较多，可能导致填充数据与实际数据存在一定的误差。

,