求对数螺线的弧长（三角形的对数螺线密铺）

女士们，先生们，老少爷们儿们！在下张大少。

本文描述了各种三角形的螺旋密铺，其中相邻的拼块以一个恒定的系数缩放。分析了较小的三角形与较大的三角形相配的不同方式，并给出了单螺旋臂和多螺旋臂的例子。对不同的可能性进行了诸多探索，发现了许多以前没有报道过的密铺。这些密铺在其中心包含一个奇异的点，在那里三角形变得无限小。除了其固有的美感，这些结构还可用于数学艺术、雕塑和建筑。

螺旋密铺

螺旋是一条从一个点出发的曲线，在围绕该点旋转的过程中向远处移动。虽然很难精确定义什么是螺旋形密铺，但一个可行的定义是，从一个固定的点沿螺旋形曲线发出的密铺，位于离该点较远的拼块较大。螺旋形拼块通常在中心包含一个单点。任何圆盘，无论多小，以单点为中心，都会遇到无限多的拼块[1]。

在这些密铺中，单点的存在使它们对密铺纯粹主义者来说不那么有趣。另一方面，螺旋线在审美上与人们产生了强烈的共鸣。除了美丽之外，它们还象征着无限，并能创造一种深度的幻觉。埃舍尔（M.C. Escher）在他的一些版画作品中加入了螺旋线[2]。

大多数螺旋形密铺可以被大致描述为阿基米德式或对数式，关键的区别在于密铺的大小是否随着离中心的距离增加而增加。对数螺旋形密铺是指那些类似的密铺以一个恒定的因素进行缩放的螺旋形密铺。在阿基米德螺旋形拼块中，所有的拼块都是全等的。我在这里描述了各种以前未知的三角形的对数螺旋拼块。参考文献[1]和[3]中给出了几个阿基米德螺旋形密铺的例子。

对数螺旋密铺的一个著名例子是如图1所示的正方形的黄金螺旋，其中连续正方形之间的比例因子处于黄金比例。类似的结构也可以使用等边三角形，如图2(A)所示，其中连续三角形的比例约为1.3247，其倒数≈0.749[4]。同样值得注意的是图2(b)中所示的金色三角形螺旋。除了比例因子是黄金平均值外，等腰三角形原始植物的长边与短边之比是黄金的。这些密铺的比例因子是通过求解简单的代数方程得到的标记密铺的边长和等价的两个表达式的距离。这三种螺旋拼块已经被发现很多年了，但我不知道它们最初是什么时候被发现的，是谁发现的。

图1:正方形黄金螺旋

图2：(A)等边三角形的螺线。(B)三角形的黄金螺线

三角形是最简单的多边形，它的边数最少。虽然四边形和其他多边形的螺旋密铺也很有趣，但最简单的多边形显然是系统地探索对数螺旋密铺的起点。如下所示，三角形的情况是丰富多样的。

在这项工作的过程中，发现了一些新的螺旋形密铺。这是通过首先想象和绘制可能的结构草图，然后根据该草图写下和解决代数方程来实现的。想象构造需要洞察力和创造力，特别是对于多臂配置，而代数方程则很容易解决。下面在描述特定的密铺时，将提到作者所知道的以前的例子。一般来说，螺旋已经被广泛研究，并被用来模拟自然形态，如贝壳，但这类作品很少涉及密铺[5]。

单臂三角形螺旋线

在这一节中，我将探讨单臂的螺旋形密铺。这里考虑的密铺有相邻的三角形共享一个顶点并沿着一条边交配，连续的密铺按系数s缩放。

图3[6]显示了一个单臂螺旋形密铺的一般构造。图中显示了一个无限密铺的环形补丁；也就是说，螺旋线无限地向内延伸到奇点，向外延伸到覆盖整个平面。角度和边被标注在补丁中最大的三角形中。边c（对角C）的长度可以设置为1而不损失一般性。

图3:三角形的一般单臂螺旋密铺

设n是可与较大三角形配对的缩减三角形的数目，直到三角形与起始三角形部分共享一条边为止。在图3的例子中，n=5。我们观察到

As^n bs = 1. (1)

对于给定的C和n，有一些A和B将允许这样的拼接。为了确定A，请注意，第n个按比例排列的三角形必须旋转n个角度A，以便与最大的三角形共享一条边。通过B的额外旋转将使其回到与最大三角形相同的方向，由此我们可以写出nA B=360°，以及

A=（180° C）/（n-1）， (2)

利用B=180°-A-C的事实。

以图3为例，n = 5, C = 80°。由式(2)可知，A = 65°，B = 35°。然后可以用正弦定律来计算a和b，用方程(1)来计算s，例如，使用在线代数方程求解器。在图3中，s≈0.8805。

当A=B=C时，方程（2）变成60°=240°/（n-1），表明只有在n=5的情况下才允许有螺旋形的密铺。然后方程（1）给出了一个满足s5 s=1的比例系数，其解是塑性数的倒数，如图2（a）所示。当C = 36°和n = 3时，方程（2）得出A = 108°。正弦律给出了a的黄金分割，如图2(b)所示。

我将特别考虑等边三角形、等腰三角形和直角三角形的螺旋形拼块。虽然只有一种使用等边三角形的螺旋形拼法，但有无限多的等腰三角形和直角三角形的螺旋形拼法。首先考虑等腰三角形的情况，有三种不同的方式将两个等腰三角形配成这样的螺旋形。如图4所示，它们是侧对侧、侧对基和基对侧。

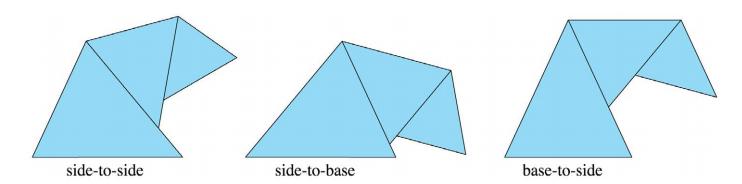
图4：在螺旋形拼接中，较小的等腰三角形与较大的等腰三角形配对的三种可能性。

如Waldman[7]所示，在侧向匹配的情况下，任何n>2的情况下都允许螺旋形拼接，他独立探索了其中一些相同的配置[8]。方程（2）简化为C=180°（n - 2）/（2n - 1）。前四种显示在图5中，可以看出，n=3产生了黄金三角螺旋，n=5产生了等边三角形螺旋。

图5:允许侧对侧匹配的前四个螺旋密铺，每个都由n唯一确定。

对于侧面与底面的匹配，任何n>3的情况下都允许有螺旋形的密铺。 方程（2）简化为C=180°（n-3）/（n 1）。前四种中的三种显示在图6中；n=5再次产生了等边三角形的螺旋形。

图6:三种螺旋密铺允许边到底匹配，每一种都由n唯一确定

对于基底-侧面匹配，任何n>4的螺旋形拼块都是允许的。公式（2）简化为C = 180°/(n - 2). 前四种中的三种显示在图7中；n=5再次产生了等边三角形螺旋。

图7：三个允许的底面与侧面匹配的螺旋形密铺，每个都由n唯一决定

类似于等腰三角形的情况，在这种密铺中有三种匹配两个直角三角形的可能性，如图8所示。对于第一种，如图8(a)所示，式(2)简化为a = 270°/(n - 1)，前四个螺旋拼块如图9所示。

图8:在螺旋密铺中，将较小的直角三角形与较大的直角三角形结合的三种可能性。

对于图8(b)的排列，式(2)简化为C = 90°(n - 3)/n。前四个螺旋贴片如图10所示。请注意，相同的三角形允许密铺两个直角三角形配置。对于图8(c)的排列，式(2)简化为c = 90°(n - 3)，由于c必须严格在0°和90°之间，我们不能使用这种排列创建任何螺旋。

在这种情况下，90°并没有什么特别之处。如果选择另一个角度，如80°，仍然会有允许的螺旋形密铺的系列。如果选择A作为控制角，那么从方程（2）来看，A角必须大于180°/（n - 1），因为C必须大于0°。回顾方程(2)是根据观察到的nA B=360°得出的。从图3可以看出，当B处于最小值时，A将处于最大值。由于B必须大于0°，A的最大值必须小于360°/n。因此，A必须位于180°/(n - 1) < A < 360°/n的范围内。例如，当n=5时，45°<A<72°。图11显示了A覆盖这一范围的大部分的螺旋形倾斜的例子。

图9：腿对斜边匹配所允许的前四个螺旋密铺

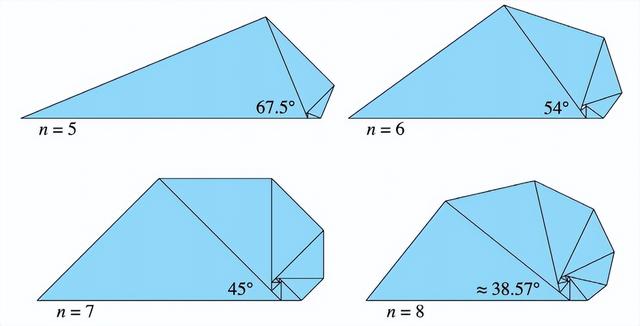
图10：斜边对腿匹配所允许的前四个螺旋密铺

图11：n=5的8个螺旋形密铺，三角形原型密铺的角度不同

请注意，通过连接每块密铺上的相同点而形成的密铺与原始密铺是一样的[8]。其结果是观察到这些密铺是自对偶的，其中对偶密铺是通过连接相邻密铺的中点产生的。图12中显示了两个例子。

图12：通过连接每个三角形中的同一点所做的螺旋形密铺与起始密铺相同。

多臂螺旋三角形

螺旋密铺可以有多个臂。事实上，上一节中的所有单臂螺旋线也都是多臂螺旋线，臂数由n给出。这在图11的69°螺旋线中很明显，大脑强烈希望将密铺解释为五臂螺旋线。前面部分中的所有密铺都有一个随着密铺变小而顺时针旋转的手臂。随着密铺变小，由相同密铺定义的多臂螺旋线逆时针旋转。

还有一些在两个方向上都是多臂的螺旋形密铺。上面的公式（2）必须修改以描述这些倾斜，而公式（1）不需要修改。图13显示了一个双臂的例子。回顾上文，缩小的密铺需要通过角度A旋转n次才能与最大的三角形共享一条边，另外还需要通过B旋转才能使其回到与相邻的大三角形相同的方向，由此，nA B=360°。在多臂的情况下，实现下一个大三角形的方向所需的总角度是360°/m，其中m是臂的数量，所以nA B = 360°/m。注意方程（1）的关系仍然成立，方程（2）变为

A=（360/m-180° C）/（n-1）。 (3)

图13：用于说明方程（3）的双臂螺旋拼块，另一方向有8个臂，为清晰起见，其中一个臂被涂黑。

一些例子如图14所示。请注意，向相反方向旋转的螺旋线的数量是m和n的乘积。

图14：在一个方向上有3、4、5个臂的螺旋形密铺，在另一个方向上有6（一个变暗以强调它）、8、15个臂。

方程(3)有一个特殊情况，即m=n=2，给出A=C，这表明任何等腰三角形都有一个允许的螺旋图式。图15中显示了几个例子。从几何上看，这对任何等腰三角形都有效，因为下一代小密铺的包络是一个平行四边形，通过共享两个角和部分共享一条边而适合于一个较大的平行四边形。

图15：可以为等腰三角形原型的连续范围的边角构造一个双臂密铺系列

当n=1时，正m形允许m臂螺旋密铺，角度A和B的连续范围。角C适合于正m形的角，值为180°-360°/m。等边三角形的情况如图16所示，正方形的情况如图17所示。从几何上讲，这是可行的，因为下一代较小的密铺的面片的包络是一个规则的m形，它相对于较大的m形旋转，与m点相接。在几何上，这是可行的，因为下一代较小的密铺的面片的包络是一个规则m形，它相对于较大的m形旋转，与m点相接。图18中显示了基于图16的第三个密铺的周期性密铺，没有奇点，以及基于三角形的四重螺旋密铺的埃舍尔设计。基于旋转的正多边形的螺线已经知道有一段时间了[9]。

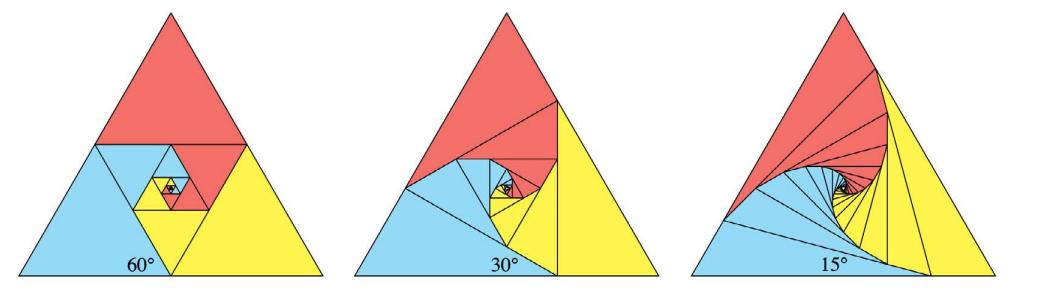
图16：从规则的三边形创建的三臂螺旋线密铺

图17：从规则的四边形创建的四臂螺旋密铺

图18:基于图16的右螺旋密铺的周期性镶嵌，以及基于直角三角形的四螺旋的埃舍尔镶嵌(几何模板不包括在这里)。

总结和结论

我已经介绍了各种各样的三角形螺旋密铺，其中许多以前没有报道过。除了它们的数学趣味性和内在美感之外，这种拼图还有许多应用。这些包括视觉数学校样、通过给密铺上色或装饰密铺(例如，使用埃舍尔的细节或打结图形)的平面设计和数学艺术，以及雕塑和建筑形式。一个需要进一步探索的领域是系统地考虑四边形、五边形等螺旋密铺的可能性。

参考文献

[1] B. Grünbaum and G.C. Shephard. Tilings and Patterns. W.H. Freeman, 1987.

[2] Bool, F.H., J.R. Kist, J.L. Locher, and F. Wierda. M.C. Escher: His Life and Complete Graphic Work. Harry N. Abrams. 1982.

[3] R.W Fathauer. Tessellations: Mathematics, Art, and Recreation. CRC Press. 2021.

[4] I. Stewart. “Tales of a Neglected Number.” Scientific American, vol. 274, no. 76, 1996, pp. 92-93.

[5] J. Picado. Seashells: the plainness and beauty of their mathmatical description. 2010.https://www.maa.org/sites/default/files/images/upload_library/23/picado/seashells/index.html.

[6] Private discussions with Dale Walton were helpful in developing some of these ideas.

[7] C. Waldman. Gnomon is an Island. 2016. http://old.nationalcurvebank.org/gnomon/gnomon.htm.

[8] C. Waldman. Private communication.

[9] Weisstein, Eric W. Polygonal Spiral. MathWorld –A Wolfram Web Resource. 2021.

https://mathworld.wolfram.com/PolygonalSpiral.html.

[10] Robert W. Fathauer, Logarithmic Spiral Tilings of Triangles

青山不改，绿水长流，在下告退。

转发随意，转载请联系张大少本尊。

,