知道三角形周长算面积例题（求三角形面积初三第4周）

求三角形的面积是初中阶段的主旋律，随着学习的深入，求三角形面积的方法逐渐向解析的方向靠拢，接下来我们来梳理一下初中求三角形面积的方法：

1.已知三边的长度求三角形的面积：利用勾股定理建方程求高。

例：如图所示，ABC的三边分别为13，14，15，求的面积。

设,则，CD是两个直角三角形的公共边，故可建方程如下

解得,

故

2.格点图中的面积的计算

例：如图所示网格的长度为1，求的面积

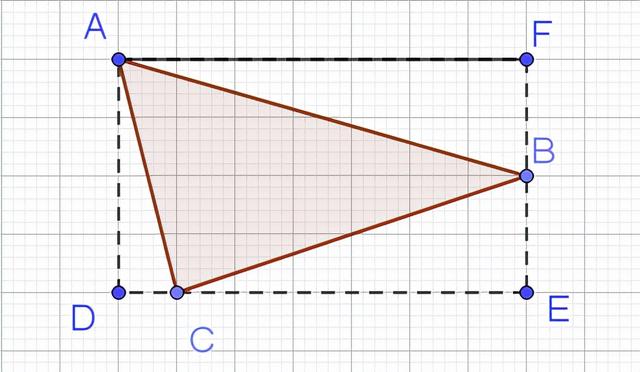
这种题目大部分学生在初一掌握的较好，就是在网格图中将其补成矩形，然后用矩形的面积剪掉三个小直角三角形的面积

3.将网格图改为坐标系

（1）将网格改为坐标系，从原理上并没有发生实质的变化，网格中的长度体现在小方格的大小，而坐标系中的长度体现在点的坐标中，网格中的三角形面积计算，三角形的顶点都是在格点处，横向与纵向长度均是整数值，因此学生并不太觉得困难，但是在坐标系下，由于学生对坐标的长度属性理解并不深刻，导致学生觉得困难，在这里

，,,

,,,

因此只需要知道的三点坐标便可求得面积。

（2）当然，上面三角形的面积除了上述的补形之外，还可以切割，在坐标系下为了表示长度的便利，可以用水平线或者竖直线进行切割

水平切割

竖直切割

在水平切割下，

在竖直切割下，

例：如图：O为坐标原点，二次函数与一次函数的图像交于两点（在的左侧），求

解：联立方程得

解得,

故.

考虑一次函数,令,得，

故

变式：将上例中一次函数解析式改为，会有什么变化呢？

本质上并没有变化，但是在联立方程得到的一元二次方程为：

此方程相较于，虽然只是改动一个小小的数，但是此时方程的解却只能用求根公式求得

这样使得计算量大增。

注意到，关键在于求得,求这个量是否必须分别

求出这两点的坐标呢？

实际上，这里可以借助韦达定理来整体求解：

上面的方法是基于韦达定理整体计算坐标之差，是高中解析几何的基础，在这里让初中生去体会整体求值的思想也是更好的为高中的解析几何打下基础，埋下伏笔。