分式方程无解和增根原因（浅谈分式方程的增根和无解）

当碰到含有参数的分式方程的增根、无解问题时，同学们在解决该类题的时候要不就是漏解，要不就是无从下手，各种问题层出不穷，对基本的增根、无解概念不熟悉。基于此，特写本文用于解决同学们碰到的这类问题，读完本文后希望同学们在考试中能精准解题。

基本概念：

1、分式方程的增根是指：分式方程化成整式方程后，整式方程有解，但是该解使得分式方程的分母为0。

2、分式方程无解是指：分式方程化成整式方程后：

①整式方程无解；

②整式方程有解，但是该解刚好使得分式方程的分母为0，是增根，导致分式方程也无解。

【关于整式方程无解的问题，请各位同学记住一个例子：】

关于x的方程：ax = 1在何时无解？

答：当a=0时无解；当a≠0时，解为

以具体引例来看：

例一、解分式方程：

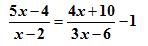
解：两边同乘以3（x-2）,得

3（5x-4）=4x 10 - 3（x-2）

解之得 x = 2

分析：

x＝2是原方程的解吗？

不是！当x＝2时，恰好使原分式方程中的分母等于0，从而使分式方程无意义．这样的根就叫做原分式方程的增根．

那么，解分式方程产生增根的原因是什么呢？

增根的产生是在解分式方程的第一步“去分母”时造成的，这一步必须满足方程的两边都乘(或除以)的是同一个不为0的数．而当x＝2时，相当于原分式方程的两边都乘的数是0，那么变形前后的方程就不是同解方程了．

因此，上面求得的根只能是原方程的增根．

由此可知，增根有两条重要性质：

1、增根是去分母后所得整式方程的根．

2、增根使最简公分母等于0．

由此，我们应该在解出分式方程后，作必不可少的一步工作，那就是检验，验根．

更多精彩内容请参考下图：