spss的方差分析结果（方差分析之趋势检验）

【作者介绍】李志辉，长期从事各类统计软件应用研究，主编或参编SPSS、MINITAB、STATISTICA多个统计软件教材共8本。代表作：电子工业出版社《SPSS常用统计分析教程(SPSS 22.0中英文版)(第4版)》（2015年）。

有网友问方差分析可以做趋势检验吗?比如想知道研究对象的指标是否随着年龄的增长有变化趋势时，是否可以用趋势检验得到答案呢？其实SPSS是提供了解决办法的。

〖例题〗已知97名幼儿的体检资料，已建立数据文件child.sav，试按年龄组（age)对坐高（x6，cm）进行方差分析并做趋势检验。

一、数据格式

1、x6（坐高）为数值变量。

2、age（年龄组)为数值变量，共有3个年龄组，其值标签分别为：5-5周岁；6-6周岁；7-7周岁。

二、方差分析

步骤：选择【分析（Analyze）】→【比较平均值（Compare Means）】→【单因素ANOVA（One-Way ANOVA）…】

当因子变量为有序变量时，选择多项式（Polynomial），可进行趋势检验，可将组间平方和划分为趋势成分，并检验因变量在因子变量分组顺序水平间的趋势是呈现线性变化趋势，还是呈二次、三次等多项式变化 。在此选择度（Degree，次数）下拉菜单中的线性（Linear）项。

☆Statistics（统计），选择描述性（Descriptive）和方差同质性检验（Homogeneity of variance test，方差齐性检验）。

并选择平均值图（Means plot）。

二、结果分析

1、描述性（Descriptives）表，5岁组、6岁组、7岁组儿童的坐高平均值分别为58.888、61.424、64.650。

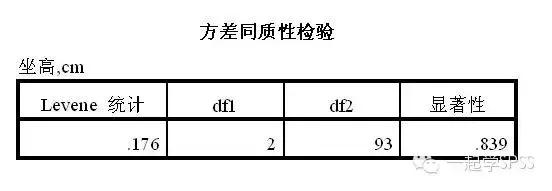
2、方差齐性检验（Test of Homogeneity of Variances）表，Levene统计量（Levene Statistic）为0.176，P=0.839>0.10，按α=0.10水准，可认为3个年龄组儿童坐高的总体方差齐。

3、方差分析（ANOVA）表（红字部分），F=36.767，P=0.000<0.05，按α=0.05水准，故可认为3个年龄组儿童坐高的总体平均值不全相等，各组方差齐时，应采用F检验的结果。

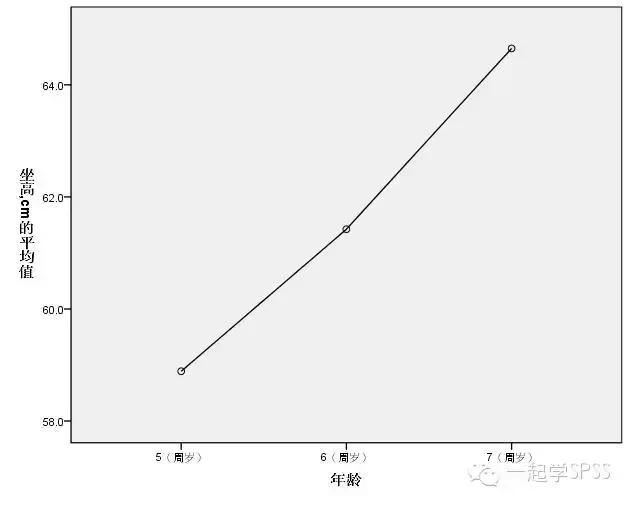
4、趋势检验的线性项（Linear Term）（蓝字部分），F=68.402，P=0.000<0.05，按α=0.05水准，可认为儿童坐高随着年龄的增长呈现线性变化趋势，平均值图（Means Plots）显示：儿童坐高与随着年龄的增长呈上升的线性趋势，两者的结果是一致的。

理论上类似的因子变量为有序变量的情况都可以进行趋势检验，如因子变量为不同药物浓度水平、接触有害因素时间的长短等都可以进行趋势检验，但有个前提条件是分析的资料要满足方差分析的条件。

获取更多的统计及统计软件知识，请关注微信同名订阅号“一起学SPSS"。