数学中考真题之线段最值问题练习（求线段长的最值有点难）

点击右上角关注“陈老师初中数理化”分享学习经验，一起畅游快乐的学习生活。

利用三角形的边长关系求解线段长度的最值问题是数学中考的常考题型，本文就例题详细解析这类题型的解题方法，希望能给初三学生的数学复习带来帮助。

如图，在边长为2的菱形ABCD中， ∠A=60°，M是AD的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A'MN，连接A'C，求A'C长度的最小值。

解题过程：

连接CM，过点C作CE⊥MD，交MD的延长线于点E

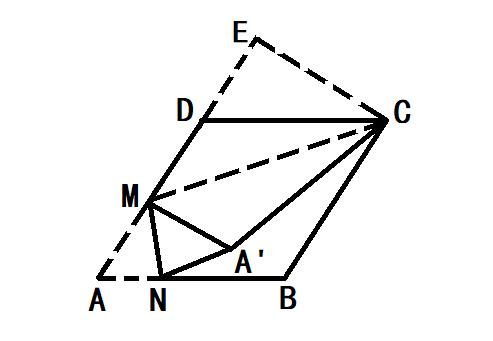
根据题目中的条件：菱形ABCD的边长为2，M是AD的中点，则AB=BC=CD=AD=2，AM=DM=AD/2=1；

根据折叠的性质和结论：AM=1，则A'M=AM=1；

根据菱形的性质：四边形ABCD为菱形，则AB∥CD；

根据平行线的性质、题目中的条件和结论：AB∥CD，∠A=60°，则∠CDE=∠A=60°；

根据三角函数值和结论：∠CDE=60°，sin∠CDE=CE/CD，cos∠CDE=DE/CD，CD=2，sin60°=√3/2，cos60°=1/2，则CE=√3，DE=1；

根据结论：DM=1，DE=1，则ME=DM DE=2；

根据勾股定理和结论：CE⊥MD，ME=2，CE=√3，CM^2=ME^2 CE^2，则CM=√7；

根据三角形的边长关系和结论：A'M=1，CM=√7，则A'C<CM-A'M=√7-1；

所以，当点A'在线段CM上时，A'C的长度能取到最小值=CM-A'M=√7-1。​

解决本题的关键是根据折叠性质得到线段间的等量关系，把需要求长度最值的线段置于一个含有动点的三角形，且这个三角形的两条边长固定不变，根据三角形的边长关系就可以确定，三点一线时线段能取得最值，再根据菱形性质和勾股定理求得相关线段的长度，就可以得到题目需要的值。