数据分析的基本方法和技巧（入行数据分析要知道什么是数值型数据）

数值数据是一种以数字表示的数据类型，而不是自然语言描述。有时称为定量数据，数值数据总是以数字形式收集。数值数据与其他数字形式数据类型的区别在于它能够对这些数字进行算术运算。

应用方法基于描述性统计分析，主要方法有以下几种。

我们以天津的少儿英语培训机构举例来说。数据来源 教育宝，使用爬虫抓取机构的名称和口碑。

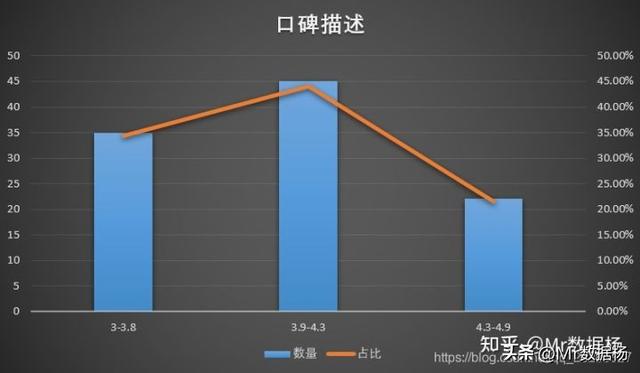
假设这100家机构入住到同一所3层大楼中，我们依照口碑如何进行楼层的划分？（虽然这种方式不太合理）

这种叫做 分组，编程语言里称作 聚合。每一层作为一个分区，称作 组 。

可以尝试计算一下每个组的一个占比情况，也称作相对次序。

相对次序 = 所属组别的个数 / 数据总数

依据这个次序分布表可以制作直方图，进行数据的可视化，表示数据间占比的情况。

算数平均数

• 也称为均值，是集中趋势的最常用测度值，是一组数据的均衡点所在，易受极端值的影响。
• 根据总体数据计算的，称为平均数，并且是个定值。
• 根据样本数据计算的，称为样本平均数。

几何平均数

• n 个变量值乘积的 n 次方根 。
• 适用于对比率数据的平均 。
• 主要用于计算平均增长率 。

排序后处于中间位置上的值。

• 不受极端值的影响。
• 主要用于顺序数据，也可用数值型数据，但不能用于分类数据。
• 各变量值与中位数的离差绝对值之和最小。
• 中位数的位置和数值。

- 中位数的应用，例如平均某城市平均工资是6000，但是3、4K的工资占绝大多数，这是为什么?

标准差表示一组数据中 平均离散程度的指标 。 标准差的数据区间为 [0, ∞] 。

例如两个球队某场比赛中打成平手，数值分布如下，是否能看出来哪队的平均势力更强一些？

标准差的计算公式如下：

以未分组的情况举例，因为两队的数据相互独立。

A队 = [ 38 ，73 ，86 ，90 ，111 ，124 ]

B队 = [ 71 ，84 ，85 ，89 ， 90 ， 103 ]

通过计算得到结果为 A组 = 27.5 ，B组 = 9.5 。

推断统计用于根据从样本群体中收集的数据对大量群体进行预测或推断。

• 趋势分析：趋势分析是一种区间数据分析技术，用于通过捕捉一定时期内的调查数据来得出趋势和洞察。
• SWOT 分析： SWOT 是优势、劣势、机会和威胁的首字母缩写词。优势和劣势用于内部分析，而机会和威胁用于组织的外部分析。
• 联合分析：这是一种市场研究分析技术，用于调查人们如何做出选择。
• TURF 分析：这是 Total Unduplicated Reach and Frequency analysis 的首字母缩写词，用于评估产品或服务组合的市场潜力。

离散数据表示可数项，可以采用数字和分类形式，具体取决于使用情况。采用可以分组到列表中的值，其中列表可能是有限的或无限的。 无论是有限的还是无限的，离散数据都采用从 1 到 10 或从 1 到无穷大的数，这些数组分别是可数有限和可数无限的。

表示测量值的数值数据，值被描述为实数线上的间隔，而不是计数。例如 5分评分系统中的累积平均绩点（CGPA）将一等学生定义为 CGPA 低于4.50 - 5.00，二等高为3.50 - 4.49，二等低为2.50 - 3.49，三等学生为 1.5 - 2.49，通过为 1.00 - 1.49，失败为 0.00 - 0.99，以此类推

连续数据可以细分为两种类型，即间隔和比率数据。

• 区间数据：是一种沿刻度测量的数据类型，其中每个点彼此之间的距离相等。区间数据采用只能进行加减运算的数值。 例如以摄氏度或华氏度测量的物体温度被视为区间数据。这个温度没有零点。
• 比率数据：是一种类似于区间数据的连续数据类型，但具有零点。换言之比率数据是零点的区间数据。 对于比率数据，温度不仅可以用摄氏度和华氏度测量，还可以用开尔文测量。零点的存在适应了 0 开尔文的测量。

• 类别：数值数据两个主要类别即离散和连续数据。连续数据进一步分解为区间和比率数据。
• 定量性：由于其定量性质，数值数据有时被称为定量数据。与采用具有定性特征的定量值的分类数据不同，数值数据表现出定量特征。.
• 算术运算：可以对数值数据执行算术运算，例如加法和减法。就其定量特征而言，几乎所有统计分析都适用于分析数值数据。
• 估计和枚举：数值数据既可以估计也可以枚举。在数值数据准确的情况下可以列举，但是如果不准确则估计数据。例如在计算学生的 CGPA 时，4.495623 CGPA 向上舍入为 4.50。
• 间隔差异：数值数据尺度上每个间隔之间的差异相等。例如挂钟上的 5 分钟和 10 分钟之间的差异与 10 和 15 分钟之间的差异相同。
• 分析：根据研究的目的，使用描述性和推论性统计方法分析数值数据。一些描述性分析方法包括：均值、中位数、方差等。推论统计方法，如描述统计分析、趋势分析、SWOT 分析等，也用于数值数据分析。
• 数据可视化：数值数据可以根据被调查的数据类型以不同的方式进行可视化。数值数据采用的一些数据可视化技术包括：散点图、点图、堆积点图、直方图等。