如何列出排列组合（数量关系排列组合）

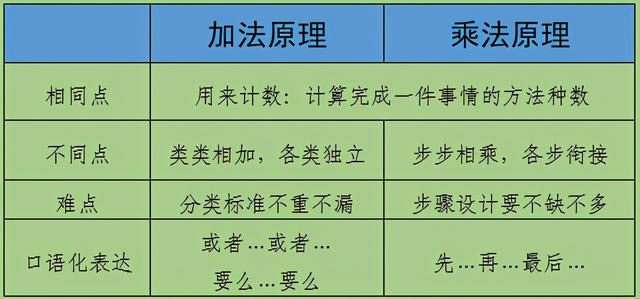
一、加法原理（分类计数原理）

每一种方法都能够直接达成目标。

二、乘法原理（分步计数原理）

分步相接，完成每步，最后才能够达成目标。

三、排列（A）与组合（C）

排列：“与顺序有关”，主体交换顺序视为不同的情况。组合：“与顺序无关”，主体交换顺序视为相同的情况。

四、捆绑法

指定的主体元素全在一起，先排整体（捆绑），再排内部（解绑）。

五、插空法

指定的主体元素全都不能在一起，先排列无要求主体，然后把不能在一起的元素插空到已经排列好的元素中间。

六、环形排列

n 个元素围成一圈的排列方式数。七、分组问题

分组问题可以分为两大类，一类是不平均分组，一类是平均分组。

八、隔板法

相同的主体元素分成数量不等的若干组，要求每组至少一个元素，则将隔板插入元素之间， 计算出分类总数。

九、错位排列

题干要求 n 个元素的位置都不在原来位置上。

十、枚举法

满足题目要求没有普遍规律，可以一一列举。

十一、反向法

正面求解困难，可以采用反向计算。