中考数学几何相关的实际应用题 几何图形中的相关计算

几何图形的折叠、平移、旋转的计算是历年中考的命题热点，本节将对此类问题作统一归纳总结 .

类型一：折叠问题

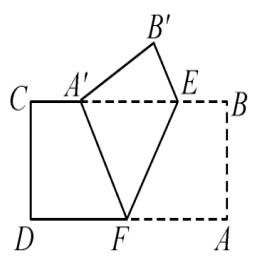
【例题1】如图，把矩形纸片 ABCD 沿 EF 翻折，点 A 恰好落在 BC 边的 A' 处，

若 AB = √3，∠EFA = 60°，则四边形 A'B'EF 的周长是 （ ）.

A、1 3√3 B、3 3√3 C、4 √3 D、5 √3

【解析】

由折叠性质可知，∠EFA = ∠EFA' = 60°，

∵ 四边形 ABCD 是矩形，

∴ BC∥AD，

∴ ∠A'EF = ∠EFA = 60°，

∴ △A'EF 为等边三角形，

∴ A'F = EF .

又 ∵ ∠B'A'F = ∠A = 90°，

∴ ∠B'A'E = 30° .

∵ A'B' = AB = √3 ,

∴ B'E = 1 , A'E = 2 ,

∴ C四边形A'B'EF = A'B' B'E A'F EF = √3 1 2 2 = 5 √3 .

故选 D .

【注解】

在解答此类问题时，关键是弄清 “折叠” 的特点：

认识到折痕两边的图形是全等的，可以得到相等的线段，相等的角 .

若图形中存在直角三角形，解题往往要结合勾股定理或直角三角形边角关系来解决；

若没有且无法构造直角三角形，则往往通过角的关系或边的等量关系来求线段长或角度 .

【拓展提高】

1、如图，将 △ABC 折叠，使点 A 与 BC 边中点 D 重合，折痕为 NM .

若 AB = 9 , BC = 6 , 则 △DNB 的周长为 （ A ）

A、12 B、13 C、14 D、15

2、对角线长分别为 6 和 8 的菱形 ABCD 如图所示，点 O 为对角线的交点，过点 O 折叠菱形，

使 B , B' 两点重合，MN 是折痕 . 若 B'M = 1 ， 则 CN 的长为 （ D ）

A、7 B、6 C、5 D、4

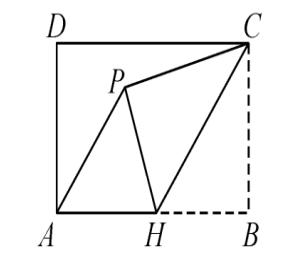
3、如图，在矩形 ABCD 中，AB = 3 , BC = 2 , H 是 AB 的中点，将 △CBH 沿 CH 折叠，

使点 B 落在矩形内点 P 处，连接 AP，则 tan∠HAP = --------4/3------.

类型二：平移问题

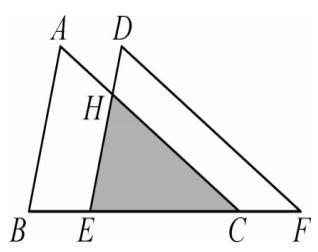
【例题2】如图，把 △ABC 沿着 BC 方向平移到 △DEF 的位置，它们重叠部分的面积是 △ABC 面积的一半，若 BC = √3，则 △ABC 移动的距离是 （ ） .

A、√3/2 B、√3/3 C、 √6/2 D、√3 - √6/2

【解析】

移动的距离可以视为 BE 或 CF 的长度，

根据题意可知，△ABC 与阴影部分为相似三角形，且面积比为 2 ： 1 ，

所以 EC : BC = 1 : √2 ,

即可求出 EC = √6/2 , BE = BC - EC = √3 - √6/2 .

故选 D .

【拓展提高】

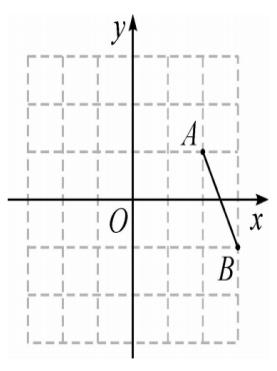
1、如图，在平面直角坐标系中，已知点 A（2,1）, 点 B（3，-1）, 平移线段 AB，

使点 A 落在点 A1（-2 , 2）处，则点 B 的对应点 B1 的坐标为 （ C ）

A、（-1，-1） B、（1 , 0） C、（-1 , 0） D、（3 ， 0）

2、如图，将 △ABE 向右平移 2 cm 得到 △DCF , 如果 △ABE 的周长是 16 cm ,

那么四边形 ABFD 的周长是 （ C ）

A、16 cm B、18 cm C、20 cm D、21 cm

3、如图，在平行四边形 ABCD 中，AD = 7 , AB = 2√3 , ∠B = 60° .

点 E 是边 BC 上任意一点，沿 AE 剪开，将 △ABE 沿 BC 方向平移到 △DCF 的位置，

得到四边形 AEFD，则四边形 AEFD 周长的最小值为 -----20--------.

类型三：旋转问题

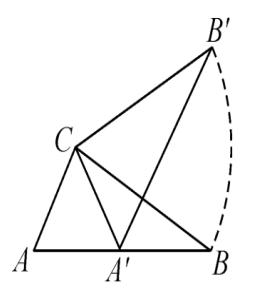
【例题3】如图，在 △ABC 中，∠ACB = 90°，∠ABC = 30°，AB = 2，

将 △ABC 绕直角顶点 C 逆时针旋转 60° 得 △A'B'C，则点 B 转过的路径长为（ ）.

A、π/3 B、√3/3 π C、2π/3 D、π

【解析】

∵ ∠ACB = 90°，

∴ △ABC 为直角三角形，

∵ ∠B = 30°，AB = 2，

∴ BC = √3 .

∵ 旋转角为 60°，即 ∠ACA' = 60°，∠BCB' = 60°，

∴ 点 B 转过的路径长是以 C 为圆心，以 BC 或 CB' 的长为半径的弧 BB' 长，

即 60π × √3 × 1/180 = √3/3 π .

故选 B .

【注解】

旋转的相关计算，关键是要掌握旋转的三大要素即旋转中心、旋转方向和旋转角度 .

在求解相关问题时，可以从以下几个方面进行考虑：

（1）求角度问题，先找旋转角，注意各对应点与旋转中心连线的夹角就是旋转角，度数相同；

（2）线段长的计算，借助旋转角将所求线段等量代换到已知图形中，结合等腰三角形，勾股定理等求解；

（3）求路径长，其实质是求弧长，需找旋转角，即弧所在扇形的圆心角 .

【拓展提高】

1、将含有 30° 角的直角三角板 OAB 如图放置在平面直角坐标系中，OB 在 x 轴上，

若 OA = 2，将三角板绕原点 O 顺时针旋转 75°，则点 A 的对应点 A' 的坐标为 （ C ）

A、（√3，-1） B、（1 , -√3） C、（√2 , -√2） D、（-√2 ， √2）

2、如图，Rt△OCB 的斜边在 y 轴上，OC = √3 , 含 30° 角的顶点与原点重合，

直角顶点 C 在第二象限，将 Rt△OCB 绕原点顺时针旋转 120° 后得到 △OC'B'，

则 B 点的对应点 B' 的坐标是 （ A ）

A、（√3，-1） B、（1 , -√3） C、（2 , 0） D、（√3，0）

3、如图，已知 △ABC 是等腰三角形，AB = AC , ∠BAC = 45°，点 D 在 AC 边上，

将 △ABD 绕点 A 逆时针旋转 45°，得到 △ACD'，且点 D' , D , B 三点在同一直线上，

则 ∠ABD 的度数是 ---------22.5°--------.

,