代数式与整式区别（代数式与整式基础知识归纳梳理）

【知识梳理】《代数式与整式》基础知识归纳梳理

【复习导语】

代数式和整式部分，是初中数学字母表示数的基础，是从具体向抽象学习的开始，涉及列代数式、求代数式的值，以及整式的有关概念和计算，主要考查学生的数感和符号意识、以及代数运算的能力，为后面的方程和函数的学习打好基础。一般中考的考查以基础题和中等题目为主，多以选择和填空的形式考查，既有常规问题，也有一些新题型，复习中需要牢固和熟练掌握整式的有关性质和运算为基础。

【知识梳理】

（一）代数式、代数式的值.

1. 代数式：用运算符号把 数和字母 连接而成的式子，单独的一个数或一个表示数的字母也叫代数式.

2. 列代数式：把问题中与 数量有关 的词语，用含有数、字母和 运算符号 的式子表示出来. 列代数式是解决方程、不等式、函数应用的基础.

注意：代数式的书写规则.

3. 代数式求值：用 具体数值 代替代数式中的字母，按运算顺序计算出的结果.

方法总结：

代数式的化简求值的几种程序

1：对已知条件进行化简或取值，直接代入求值；

2：对求的代数式进行化简，直接代入求值；

3：已知和求的式子都要变形，再代入求值.

4：整体代入法

（二）整式及整式的运算

1. 整式分为 单项式 和 多项式 ；

注意：单项式是由系数、字母、字母的指数构成的，系数不可以是带分数.

2. 同类项：所含 字母 相同，并且相同字母的 指数 也相同的项；

3. 合并同类项：只把同类项的 系数 相加，字母和字母的指数 都不变 ；

4.去括号、添括号法则：关键看括号前面的符号，括号前面是“＋”，去、添括号，括号里各项符号都 不变 ，括号前面是“－”，去、添括号，括号里各项符号都 改变 ；

5. 整式的运算：

①整式的加减：本质是去括号与 合并同类项 ；

②整式的乘法：包括单项式乘以单项式、单项式乘以多项式、多项式乘以单项式；

注意：

单项式乘以单项式结果仍然是单项式

单项式乘以多项式结果为多项式，其项数；与原多项式的项数一致；

计算时要注意符号问题，多项式的每一项要包括它前面的符号，也要注意单项式前面的符号；

多项式乘以多项式展开时，有同类项的要合并；

公式中的字母可以表示数，也可以表示单项式、多项式；

乘法分配律的正确使用，不要漏乘，关注符号；

6. 乘法公式

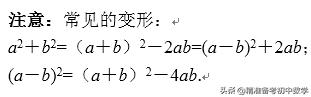
（三）幂的运算

注意：

幂的相关运算的逆向应用：

指数相加，幂要相乘；

指数相乘，幂要乘方；

指数相减，幂要相除。

（四）因式分解

1.因式分解定义：把一个多项式分解成几个整式 乘积 的形式，因式分解与整式乘法是 互逆 的运算；

2. 基本方法：

①提公因式法：ma＋mb＋mc= m(a b c) ；

关键：公因式的确定：

公因式：系数是各项系数的最大公约数字母取各项相同字母的最低次幂。提公因式时，若有一项全部提出，括号里的项为1；

②公式法：

注意：公式法的选取：

根据多项式的项数，如果是二项式，考虑平方差公式 如果是三项式考虑完全平方公式使用公式时，分清公式中的a、b才能正确套用公式；

3. 因式分解一般步骤：

一提（如果多项式有公因式，应先提公因式）

二套（尝试使用乘法公式）

、三查（检查因式分解是否彻底）

4.分解的范围：无特殊说明，因式分解在有理数范围内分解.

易错点：①分解因式不彻底，②提底数互为相反数的幂的公因式时，出现符号错误.

【在线答题】

点击左下方链接“了解更多”，参与在线答题活动，巩固练习相关知识点，让学习更有针对性！更具实效性！（说明：电脑端可直接点击链接进入答题活动，手机端点击链接后，需先自动转跳到QQ登陆后，再进行答题。可任意输入姓名符号，便于排行榜显示）

做题不再枯燥！学习更加有效！

进入备考初中数学工作室，参与在线答题

作者：精准备考初中数学，中学高级教师，教育领域创作者。从教中学数学20余年，重点研究领域：中考数学命题与复习备考、真题详解、圈题预测，初中数学教学。致力于分享教学经验和研究成果，助力考生冲刺高分！

点击左下方链接“了解更多”，进入【在线答题】活动

,