已算到31.4万亿位（已算到31.4万亿位）

目前，以最多数字背诵圆周率的吉利斯世界纪录已多次刷新，来自印度的拉杰维尔 米纳（Rajveer Meena），他在10小时内背诵了70000个数字。今天，我们就来聊聊π。

π是一个迷人的数学常数，它无视任何记忆技巧，所以你只能蛮力记住它。而当你花几天时间背诵尽可能多的数字时，数学家们已计算出新的数字。π可以通过将圆的周长除以它的直径来得到，这在纸面上很简单，但在实践中要困难得多，因为准确测量圆的周长实际上是不可能的，即使你使用卷尺进行的最佳尝试也会因卷尺的厚度而有所下降。

阿基米德是第一个用割圆法计算圆周率的人，在阿基米德的心中，圆是一个有着无数边的多边形，所以从边数较少的多边形开始，我们可以通过计算圆周与直径的比率来粗略估计π的值。

首先先在圆内放置一个正方形，它的角接触圆的边。然后我们可以通过将平方边的总和除以其对角线直径得出π的估计值比率。反过来，现在让我们放置一个正方形，它的边与圆的边接触，这一次我们将正方形边的总和除以正方形边之一的长度，得到4，即正方形的边数。在这两种情况下，我们再都除以圆直径就可以得到π，但都我们无法测量圆的周长，而内部正方形周长太小，外部正方形周长太大，我们唯一确定的是，π位于这两个数字之间。

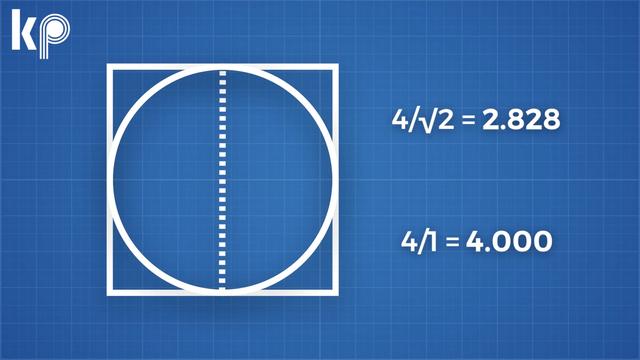
现在我们只需要缩小它的范围，我们可以通过增加多边形的边数来做到这一点。每次我们添加一个边时，这两个数字会变得更加准确，最终这两个数字的数字将开始重叠，我们得到了π的准确值。

2019年3月14日，谷歌宣布圆周率现已到小数点后31.4万亿位，这让我们不禁自问，我们真的需要小数点后31.4万亿位的圆周率码？

事实上，把圆周率的数值算得这么精确，实际意义并不大。现代科技领域使用的圆周率值，有十几位已经足够了。如果以39位精度的圆周率值，来计算可观测宇宙的大小，误差还不到一个原子的体积。以前的人计算圆周率，是要探究圆周率是否为循环小数，而自从1761年兰伯特证明了圆周率是无理数，1882年林德曼证明了圆周率是超越数后，圆周率的神秘面纱就被揭开了。

尽管如此，但π在许多数学领域都有非常重要的作用，它用于计算圆的周长和面积，而我们对于JPL的最高精度的计算，比如用于行星际导航，我们使用最多的就是3.141592653589793。

至于为什么不往后多几位数呢，原因很简单，再多几位小数，算出的结果也没有意义了。

让我们以距地球约216亿公里的探测器航海者1号为例，假设我们以这个距离为圆的半径来计算圆的周长，公式是2*π*半径，我们用圆周率小数点后15位和16位分别计算，来看它们的误差。

圆周率小数点后15位代入后周长大概为1362亿公里，如果在圆周率后多加一位小数，然后计算它们的差值，我们得出8.6763毫米，还不到一个小指头那么长。换句话说，把圆周率截取在第15位，已经让这个216亿公里半径的圆的周长误差控制在不到1厘米！而圆周率越往后，计算的差值就越小，那已经没有任何意义了。