spss单独样本t检验如何做（SPSS数据分析之配对样本T检验操作）

数据分析中，往往有些数据是成对出现的，两个样本的一种特殊状况，配对样本T检验是用于检验两配对样本总体的均值是否存在显著差异，零假设：两个配对样本的数据的均值不存在显著差异。

话不多说，直接上操纵。

原始数据

原始数据

变量视图：

小数：2；值标签：1组填写不施肥，2组填写施肥

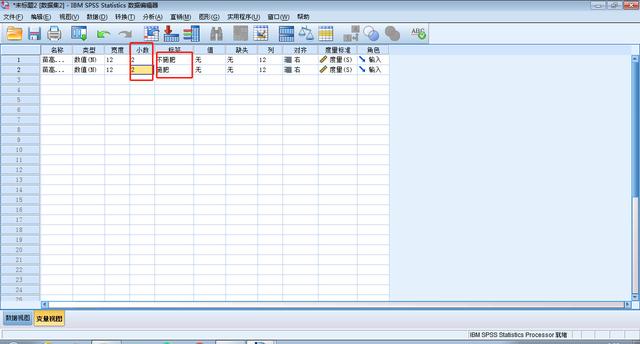
值标签

操作：分析→比较均值→配对样本T检验

配对样本T检验

选择：不施肥、施肥一对→确定

配对

输出结果

上表可知，不施肥均值2.4045，施肥均值是2.2455，两组对比的个案数均为22。

上表可知，不施肥和施肥相关性系数是0.186，显著性Sig为0.408＞0.05，说明两者配对变量之间的相关性不显著。

上表可知，不施肥减去施肥的苗高增长量平均值为0.15909，T为0.59，Sig值为0.561＞0.05，接受原假设，说明两个配对样本的均值是不存在显著差异的，即说明施肥或不施肥对苗高的增长没有太大效果。

今天的数据分析就学习到这里，有任何问题可以评论留言，如有想看的操作讲解，可以私信我。谢谢大家的点赞、关注和转发。