空间平面的向量表示式怎么理解（如何理解用数学表示的平面空间）

让我们直入主题：我们常常用π来表示一个平面:你看不懂这个公式没有关系，接下来我将把它讲明白。

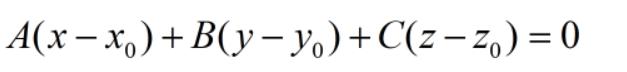
假设现在我们有一个特定点，这个点是已知的：

现在我们发现一个垂直于这个平面的向量，我们把它称作法向量：

而

是未知变量。

大家知道，一个空间中的点的坐标减去另一个空间中的点的坐标，它的意义是一个向量,我们把它记作K。

于是，一个平面就等于法向量点乘这个未知向量：

大家知道，垂直向量的点乘为0，所以有：

于是，我们可以推演出平面的一般方程：

D为常数

这个方程有什么用呢？我们现在做一个数学实验。

设有三个空间中的点A(1,0,-1),B(2,1,2),C(-1,1,3)，我们现在要设法确定它的空间平面方程。我们知道，三点确定一个平面。两条相交的直线也能确定一个平面。

于是我们准备搞出两条相交的直线来：

我们知道n向量垂直于上面这俩，所以可以直接用叉乘（右手定则）：

至于这个矩阵怎么运算的，大家可以参考我之前的文章，这里就不带大家算了。

于是，我们根据之前的定义，随便取一个点A(取B,C都可以），可以推出：

这个平面长什么样子呢，好像不直观啊！我们对它变个形状：

我们用MATLAB画出它的图，光靠三个点就能确定一个这样的平面，是不是很神奇呢？

感谢大家抽空阅读~