高中数学常见幂函数图像(高中数学幂函数的概念)
1、幂函数的概念
一般地,函数


例1、已知幂函数
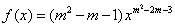


分析:正确理解幂函数的概念、幂函数的图象与性质。求幂函数的解析式,一般用待定系数法,弄明白幂函数的定义是解题的关键。
解答:由于
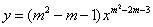
所以



当时,


当时,


故所求幂函数


2、幂函数的图象和性质
图象:

性质:
(1)所有的幂函数在上都有定义,并且图象都过点;
(2)如果



(3)如果


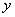
(4)当为奇数时,幂函数为奇函数;当为偶数时,幂函数为偶函数。
例2、比较
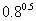
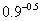
分析:先利用幂函数
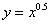
解答:


而在上单调递增,且
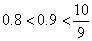
,


例3、若函数


分析:本题考查简单幂函数的性质以及函数图象的平移问题。
函数
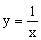



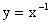
解答:由于

,所以函数的图象是由幂函数

的图象先向右平移2个单位,再向上平移3个单位得到的,所以其图象如图所示。

其单调递减区间是


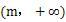

例4、若点
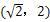

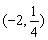


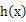
分析:首先根据幂函数的定义求出


解答:设

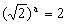

又设

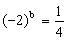

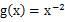
在同一坐标系下画出函数和的图象,如图所示,则有

。

根据图象可知函数的最大值等于




例5、已知幂函数

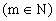

分析:先根据单调性求出m的取值范围,再由奇偶性进一步确定m的取值。讨论

解答:由在上是减函数得


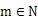

又因为是偶函数,∴只有当

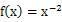
于是

,

。
当


当

当且

当且时,为既奇又偶函数。
例6、已知幂函数


(1)求的值,并写出相应的函数的解析式;
(2)对于(1)中求得的函数,设函数



分析:第一问先根据单调性求出的取值范围,再由奇偶性进一步确定的取值。第二问可根据复合函数单调性的规律来解。
解答:(1)∵幂函数


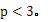
又


∵在定义域上是偶函数,∴只有当

(2)由,则

假设存在实数,使得满足题设条件。令


∵在上是减函数,∴当




若在区间上是减函数,且在区间上是增函数,则

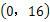



∴

。
故存在实数,使得函数在区间上是减函数,且在区间上是增函数。
,免责声明:本文仅代表文章作者的个人观点,与本站无关。其原创性、真实性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容文字的真实性、完整性和原创性本站不作任何保证或承诺,请读者仅作参考,并自行核实相关内容。文章投诉邮箱:anhduc.ph@yahoo.com